Комплексные числа

1. Изобразить на плоскости точки, соответствующие числам 5, -2, -3i, .

2. Найти вещественные числа x и y, удовлетворяющие уравнению: а) ; б) .

3. Вычислить выражения: а) (2+i)(3-i)+(2+3i)(3+4i); б) ; в) ; г) ; д) ; е) .

4. Вычислить , где n – целое число.

5. Комплексные числа представить в тригонометрической и показательной формах.

6. Найти тригонометрическую форму числа: а) 5; б) i; в) -2; г) -3i; д) (1+i); е) ; ж) ; з) sin +i cos ; и) .

7. Данные комплексные числа представить в показательной форме и выполнить действия: а) ; б) .

8. Выразить cos 3φ, sin 3φ, cos 4φ, sin 4φ через и sinφ .

9. Найти комплексные числа такие, что

10. Нарисовать линию на комплексной плоскости, заданную уравнением: а) , б) , в) , г)

11. Нарисовать на плоскости ℂ область, заданную неравенствами а) 1<|z|≤ 5; б) -1≤ Re z<0; в) 2π > Im z>0, г)

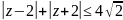
12. Изобразить на комплексной плоскости множество точек, соответствующиx условиям: а) |z|=1; в) |z-1-i|<1; г) 1≤ |z-2i|<2; д)|Re z|≤ 1; е) |z+2|-|z-2|=3.

13. Как расположены на плоскости точки, соответствующие а) комплексным числам , для которых , и ; б) комплексным числам для которых ,

14. Нарисовать кривую на комплексной плоскости.

15. Разложить многочлен двух переменных в произведение линейных многочленов над полем ℂ.

16. Найти образ единичного квадрата K: 0≤ x≤ 1, 0≤ y≤ 1 относительно отображения z→ 1/(1+z).

17. Вычислить выражения: а) ; в) ; г) .

18. Найти комплексные числа, соответствующие противоположным вершинам квадрата, если двум его соседним вершинам соответствуют числа 2+i и 5-i.

19. Изобразить на плоскости множество точек, соответствующих комплексным числам , где t∈ ℝ .

20. Доказать равенство

21. Найти все комплексные числа, сопряженные к а) своему квадрату; б) своему кубу.

22. Найти при .

23. Доказать равенства: а) (n∈ ℤ ); б) (n∈ℤ )

24. Решить уравнения над полем комплексных чисел:

    1. ;

    2. ;

    3. ;

    4. (4+i)z+7i=1;

    5. ;

    6. ;

    7. ;

    8. ;

    9. ;

    10. .

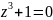25. Решить уравнения: а) , б) .

26. Решить систему уравнений:

    1. , ;

    2. ; ;

    3. , .

27. Доказать, что:

    1. если |z|<1, то ;

    2. если |z|≤ 2, то ;

    3. если |z|<1/2, то .

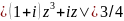28. Доказать неравенство: .

29. Доказать, что если , то , где n∈ ℤ .

30. Доказать равенство:

где x≠ 2kπ, k∈ ℤ

31. Доказать, что если комплексное число z является одним из корней степени n из вещественного числа a, то и сопряженное число является одним из корней степени n из a.

32. Вычислить все комплексные корни: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .

33. Найти двумя способами корни степени 5 из единицы и выразить в радикалах и . Как следствие получить способ построения правильного пятиугольника с помощью циркуля и линейки.

34. Решить уравнения: а) ; б) .

35. Является ли число корнем некоторой степени из единицы?