8) Случайная величина называется непрерывной, если ее функция распределения f(X) непрерывна на всей числовой оси.

Для непрерывной случайной величины   при любом   имеет место равенство

а также

где F(x) функция распределения величины   .

Пусть f(x) - неотрицательная интегрируемая функция, определенная на всей числовой оси и удовлетворяющая условию

Тогда функция

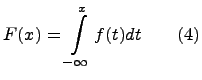
обладает всеми свойствами функции распределения. Кроме того, F(x) непрерывна в любой точке (и слева, и справа). Следовательно, случайная величина   , определяемая функцией распределения F(x), является непрерывной.

Мы говорим, что случайная величина   с функцией распределения F(x) раcпределена сплотностью, если существует неотрицательная функция f(x), такая, что для любого  имеет место равенство (2). При этом f(x) называется плотностью вероятности случайной величины   , а ее график – кривой распределения.

Из определения плотности вероятности f(x) и свойств функции распределения следует, что f(x) должна удовлетворять условию (1). И обратно, если   и выполняется условие (1), то f(x) является плотностью вероятности.

Если случайная величина   имеет плотность вероятности f(x) , то имеет место формула

функция распределения и плотность распределения непрерывной случайной величины, их взаимосвязь и свойства. Равномерное распределение вероятностей.

Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) – F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.

Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифферен-циальная функция).

Определение 5.1. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле:

                                                         f (x) = F′(x),                                                           (5.1)

то есть является производной функции распределения.

                     Свойства плотности распределения.

1)      f(x) ≥ 0, так как функция распределения является неубывающей.

2)      , что следует из определения плотности распределения.

3)      Вероятность попадания случайной величины в интервал (а, b) определяется формулой                                                                            Действительно, 

4)        (условие нормировки). Его справедливость следует из того, что   а 

5)       так как   при Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины  обозначается M .

Математическое ожидание дискретной случайной величины  , имеющей распределение

 

называется величина  , если число значений случайной величины конечно.

Если число значений случайной величины счетно, то  . При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_(x) вычисляется по формуле  . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

Если случайная величина  является функцией случайной величины  ,  = f(x), то

.

Аналогичные формулы справедливы для функций дискретной случайной величины:

,  .

Основные свойства математического ожидания:

математическое ожидание константы равно этой константе, Mc=c ;

математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин  ,  и произвольных постоянных a и bсправедливо: M(a + b ) = a M( )+ b M( );

математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(  ) = M( )M( ).

 

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина  имеет математическое ожидание M , то дисперсией случайной величины  называется величина D = M( - M )².

Легко показать, что D = M( - M )²= M ² - M( )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

,  .

Для определения меры разброса значений случайной величины часто используетсясреднеквадратичное отклонение  , связанное с дисперсией соотношением  .

Основные свойства дисперсии:

дисперсия любой случайной величины неотрицательна, D   0;

дисперсия константы равна нулю, Dc=0;

для произвольной константы D(c ) = c²D( );

дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(  ) = D( ) + D ( ). Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние,станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно еёматематического ожидания. Среднеквадратическое отклонение: