
- •1.Система действительных чисел и операции над числами. Обыкновенные и десятичные дроби. Действия с дробями.
- •2.Иррациональные уравнения. Решение иррациональных уравнений.
- •3.Определители 2 и 3 порядка. Решение систем линейных уравнений по формулам Крамера. Основные случаи решений системы линейных уравнений.
- •4.Числовая последовательность. Постоянная и переменная величина. Монотонность и ограниченность последовательности. Бесконечно малая и бесконечно большая величина.
- •6.Числовая функция. Способы задания функций. Основные свойства функций.
- •8.Корень n-ой степени и его свойства.
- •10. Понятие логарифма. Основное логарифмическое тождество. Натуральные и десятичные логарифмы. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому.
- •11.Логарифмическая функция. Свойства и график функции
- •12.Показательная функция. Свойства и график функции
- •13.Решение показательных уравнений и неравенств.
- •14. Решение логарифмических уравнений и неравенств
- •18.Свойства и график
- •19.Свойства и график
- •27. Аксиомы стереометрии и следствия из них. (Следствие доказать(по выбору)
- •28. Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых (вывод).
- •29. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости (вывод)
- •30. Взаимное расположение двух плоскостей в пространстве. Признак параллельности плоскостей (вывод)
- •31. Параллельное проектирование. Свойства параллельных проекций. Изображение фигур в стереометрии.
- •32. Ортогональное проектирование. Расстояние от точки до плоскости. Симметрия в пространстве.
- •35. Двугранный угол. Угол между плоскостям. Трёхгранный угол. Многогранный угол.
- •56. Многогранник. Основные понятия. Правильные многогранники.
- •75. Площадь поверхности сферы.
- •36. Векторы в пространстве. Действия над векторами. Компланарность векторов. Разложение вектора по трем некомпланарным векторам.
- •37. Декартовы координаты. Действия над векторами, заданными координатами. Формулы для вычисления длины вектора, угла между векторами.
- •Формулы для вычисления длины вектора.
- •Формулы для вычисления угла между векторами.
- •38. Уравнение прямой на плоскости. Общее уравнение прямой, векторное, каноническое, уравнение прямой в отрезках; уравнение прямой, заданной двумя точками. Уравнение прямой на плоскости
- •Уравнение прямой в отрезках
- •Каноническое уравнение
- •Уравнение прямой, проходящей через две данные точки
- •39. Уравнение окружности. Координаты центра окружности.
- •40. Параллельность и перпендикулярность прямых, заданных уравнениями.
- •41. Приращение аргумента и приращение функции. Понятие производной функции. Вычисление производной по 4 действиям.
- •42. Геометрический и физический смысл производной. Уравнение касательной к графику функции.
- •1)Физический смысл производной.
- •2) Геометрический смысл производной.
- •43. Правило дифференцирования суммы двух функций, произведения двух функций, частного двух функций.
- •45. Понятие сложной функции. Правило дифференцирования сложной функции.
- •46. Производные тригонометрических функций.
- •47. Производная показательной и логарифмической функции.
- •59. Пирамида. Основные элементы: основание, боковое ребро, высота, боковая грань. Правильная пирамида. Усеченная пирамида.
- •60. Фигура вращения. Цилиндр. Сечения цилиндра плоскостью.
- •61. Конус. Усеченный конус. Сечение конуса плоскостями.
- •62. Шар. Сфера. Уравнение сферы.
- •63. Сечения сферы, шара плоскостью. Плоскость, касательная к сфере.
- •64. Понятие объема тела. Общие свойства объемов многогранников.
- •65. Объем прямоугольного параллелепипеда. Объем произвольной призмы (вывод).
- •66. Объем пирамиды (вывод). Объем усеченной пирамиды.
- •67. Объем цилиндра (вывод)
- •69. Объем конуса(вывод). Объем усеченного конуса.
- •70. Объем шара (вывод). Объем шарового сектора, объем шарового сегмента.
- •49. Критические точки функции. Теорема существования экстремумов функции.
- •57. Призма. Основные элементы: основания, боковое ребро, высота, боковая грань, диагональ, диагональное сечение. Правильная призма.
- •58. Параллелепипед и его свойства.
- •33. Угол между прямой и плоскостью. Теорема о трёх перпендикулярах (доказать)
- •34. Перпендикулярность прямой и плоскости. Признак препендикулярности прямой и плоскости (доказать).
8.Корень n-ой степени и его свойства.
Свойства корней:
 =
=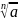 *
*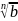
 =
=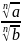
 =
=
=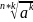
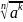 =
= k
k
Определение:
– называется такое число n, степень которого равна а.
равно b, =b, =a
Арифметическим корнем n степени из числа а называется не отрицательное число, n степень которого равна а.
При нечетном n существует корень n степени, из любого числа а, и при том только один.
Дли
любого действительного х,

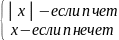
Свойства:
= *
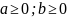
Корень n-степени из произведения неотрицательных со-множителей равен произведению корней из этих со-множителей.
=

Корень n-степени из дроби с не отрицательным числителем и положительным знаменателем равен отношению корней из числителя и знаменателя.
=

Чтобы извлечь корень и корня достаточно перемножить показатели корней.
=
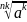
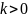
Основное свойство корня n-степени. Показатель корня и показатель подкоренного выражения можно разделить на одно и то же положительное число.
 =
=

Чтобы корень n-степени возвести в степень, достаточно подкоренное выражение возвести в эту степень, а затем извлечь корень.
9.Степень с произвольным действительным показателем. Основные свойства.
Степени с действительными показателями обладают теми же свойствами, что и степени с натуральным показателем. Сформулируем их. Пусть а,b некоторые положительные действительные числа;r,r1,r2- произвольные действительные числа.
Основные свойства:
1.ar1.ar2=ar1+r2
При умножении степеней с одинаковым основанием , основание остается прежним, а показатели складываются.
2.ar1/ar2=ar1-r2
При делении степеней с одинаковым основанием, основание степени сохраняется, а показатели вычитаются.
3.(ar1)r2=ar1.r2
При возведении степени в степень, основание степени сохраняется, а показатели перемножаются.
4.(ab)r=ar.br
При возведении произведения в степень надо каждый множитель возвести в эту степень.
5.(a\b)r=ar\br, b не равно 0
При возведении дроби в степень, надо числитель и знаменатель возвести в эту степень, при условии, что знаменатель дроби не равно 0.
Замечание!
Все 5 формул применяются как слева направо, так и справа налево.
10. Понятие логарифма. Основное логарифмическое тождество. Натуральные и десятичные логарифмы. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому.
Логарифмом
числа b по
основанию a
определяется как показатель
степени,
в которую надо возвести основание a,
чтобы получить число b.
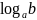 =c;
=c;
 =b
=b
Основное
логарифмическое тождество:
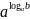 =b
=b
Десятичные
логарифмы (логарифмы по основанию 10)
 обычно обозначают lg
a
обычно обозначают lg
a
Натуральные
логарифмы (логарифмы по основанию
e=2,718281828)
 обычно обозначают
обычно обозначают

Основные свойства логарифмов:
 =1
=1

 =
k
=
k
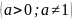
 =
=
 +
+

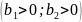
 =
-
=
-
 =c
=c
Формулы перехода от одного основания к другому:
 =
=
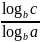
=

11.Логарифмическая функция. Свойства и график функции
Функция
заданная формулой
называют логарифмической функцией по
основанию а.
 .
Функция является строго
возрастающей при a >
1 и
строго убывающей при 0
< a <
1. График любой
логарифмической функции проходит через
точку (1;0).
.
Функция является строго
возрастающей при a >
1 и
строго убывающей при 0
< a <
1. График любой
логарифмической функции проходит через
точку (1;0).
Свойства функции у = logaх , a > 1:
D(у) = (0; +
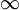 );
);не является ни четной, ни нечетной;
возрастает на (0; + );
не ограничена сверху, не ограничена снизу;
не имеет ни наибольшего, ни наименьшего значений;
непрерывна;
E(у) = (- ;+ );
выпукла вверх;
дифференцируема.
Свойства функции у = logaх , 0 < a < 1 :
|
|
