
- •1.Система действительных чисел и операции над числами. Обыкновенные и десятичные дроби. Действия с дробями.
- •2.Иррациональные уравнения. Решение иррациональных уравнений.
- •3.Определители 2 и 3 порядка. Решение систем линейных уравнений по формулам Крамера. Основные случаи решений системы линейных уравнений.
- •4.Числовая последовательность. Постоянная и переменная величина. Монотонность и ограниченность последовательности. Бесконечно малая и бесконечно большая величина.
- •6.Числовая функция. Способы задания функций. Основные свойства функций.
- •8.Корень n-ой степени и его свойства.
- •10. Понятие логарифма. Основное логарифмическое тождество. Натуральные и десятичные логарифмы. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому.
- •11.Логарифмическая функция. Свойства и график функции
- •12.Показательная функция. Свойства и график функции
- •13.Решение показательных уравнений и неравенств.
- •14. Решение логарифмических уравнений и неравенств
- •18.Свойства и график
- •19.Свойства и график
- •27. Аксиомы стереометрии и следствия из них. (Следствие доказать(по выбору)
- •28. Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых (вывод).
- •29. Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости (вывод)
- •30. Взаимное расположение двух плоскостей в пространстве. Признак параллельности плоскостей (вывод)
- •31. Параллельное проектирование. Свойства параллельных проекций. Изображение фигур в стереометрии.
- •32. Ортогональное проектирование. Расстояние от точки до плоскости. Симметрия в пространстве.
- •35. Двугранный угол. Угол между плоскостям. Трёхгранный угол. Многогранный угол.
- •56. Многогранник. Основные понятия. Правильные многогранники.
- •75. Площадь поверхности сферы.
- •36. Векторы в пространстве. Действия над векторами. Компланарность векторов. Разложение вектора по трем некомпланарным векторам.
- •37. Декартовы координаты. Действия над векторами, заданными координатами. Формулы для вычисления длины вектора, угла между векторами.
- •Формулы для вычисления длины вектора.
- •Формулы для вычисления угла между векторами.
- •38. Уравнение прямой на плоскости. Общее уравнение прямой, векторное, каноническое, уравнение прямой в отрезках; уравнение прямой, заданной двумя точками. Уравнение прямой на плоскости
- •Уравнение прямой в отрезках
- •Каноническое уравнение
- •Уравнение прямой, проходящей через две данные точки
- •39. Уравнение окружности. Координаты центра окружности.
- •40. Параллельность и перпендикулярность прямых, заданных уравнениями.
- •41. Приращение аргумента и приращение функции. Понятие производной функции. Вычисление производной по 4 действиям.
- •42. Геометрический и физический смысл производной. Уравнение касательной к графику функции.
- •1)Физический смысл производной.
- •2) Геометрический смысл производной.
- •43. Правило дифференцирования суммы двух функций, произведения двух функций, частного двух функций.
- •45. Понятие сложной функции. Правило дифференцирования сложной функции.
- •46. Производные тригонометрических функций.
- •47. Производная показательной и логарифмической функции.
- •59. Пирамида. Основные элементы: основание, боковое ребро, высота, боковая грань. Правильная пирамида. Усеченная пирамида.
- •60. Фигура вращения. Цилиндр. Сечения цилиндра плоскостью.
- •61. Конус. Усеченный конус. Сечение конуса плоскостями.
- •62. Шар. Сфера. Уравнение сферы.
- •63. Сечения сферы, шара плоскостью. Плоскость, касательная к сфере.
- •64. Понятие объема тела. Общие свойства объемов многогранников.
- •65. Объем прямоугольного параллелепипеда. Объем произвольной призмы (вывод).
- •66. Объем пирамиды (вывод). Объем усеченной пирамиды.
- •67. Объем цилиндра (вывод)
- •69. Объем конуса(вывод). Объем усеченного конуса.
- •70. Объем шара (вывод). Объем шарового сектора, объем шарового сегмента.
- •49. Критические точки функции. Теорема существования экстремумов функции.
- •57. Призма. Основные элементы: основания, боковое ребро, высота, боковая грань, диагональ, диагональное сечение. Правильная призма.
- •58. Параллелепипед и его свойства.
- •33. Угол между прямой и плоскостью. Теорема о трёх перпендикулярах (доказать)
- •34. Перпендикулярность прямой и плоскости. Признак препендикулярности прямой и плоскости (доказать).
67. Объем цилиндра (вывод)
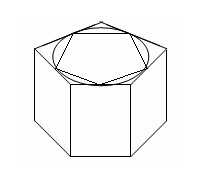 Найдем
объем цилиндра с радиусом основания R
и высотой H.
Построим две прямые
призмы с высотой H такими, что основание
одной призмы является n-угольник,
содержащий круг, а основание второй
призмы n-угольник, содержащийся в круге.
Тогда первая призма содержит цилиндр,
а вторая призма содержится в цилиндре.
При неограниченном увеличении n площади
многоугольников приближаются к площади
круга S(основанию цилиндра) и, следовательно,
их объемы неограниченно приближаются
к SH. Тогда
Найдем
объем цилиндра с радиусом основания R
и высотой H.
Построим две прямые
призмы с высотой H такими, что основание
одной призмы является n-угольник,
содержащий круг, а основание второй
призмы n-угольник, содержащийся в круге.
Тогда первая призма содержит цилиндр,
а вторая призма содержится в цилиндре.
При неограниченном увеличении n площади
многоугольников приближаются к площади
круга S(основанию цилиндра) и, следовательно,
их объемы неограниченно приближаются
к SH. Тогда
![]() Объем
цилиндра равен произведению площади
основания на высоту.
Объем
цилиндра равен произведению площади
основания на высоту.
69. Объем конуса(вывод). Объем усеченного конуса.
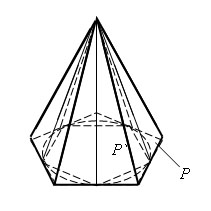
Построим
два многоугольника в плоскости основания
конуса: многоугольник P, содержащий
основание конуса, и многоугольник P`,
содержащийся в основании конуса. Построим
две пирамиды с основаниями P и P` и вершиной
в вершине конуса. Первая пирамида
содержит конус, а вторая пирамида
содержится в конусе.
Существуют
такие многоугольники P и P`, площади
которых при неограниченном увеличении
числа их сторон n неограниченно
приближаются к площади круга в основании
конуса. Для таких многоугольников объемы
построенных пирамид неограниченно
приближаются к 1/3 SH, где S – площадь
основания конуса, а H – его высота.
Согласно определению отсюда следует,
что объем конуса
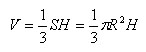 Объем
конуса равен одной трети произведения
площади основания на высоту.
Объем
конуса равен одной трети произведения
площади основания на высоту.
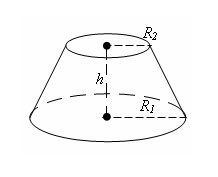 Пусть
есть усеченный конус с радиусами
оснований R1 и R2 (R2
Тогда объем
усеченного конуса равен:
Пусть
есть усеченный конус с радиусами
оснований R1 и R2 (R2
Тогда объем
усеченного конуса равен:
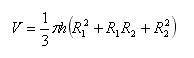
70. Объем шара (вывод). Объем шарового сектора, объем шарового сегмента.
Применяя
формулу для объема тел вращения вычислим
объем шара.
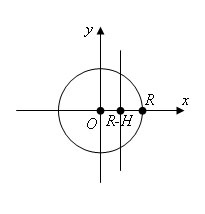
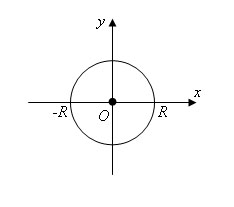 Введем
декартовы координаты, приняв центр шара
за начало координат. Плоскость xy
пересекает поверхность шара радиуса R
по окружности, которая задается
формулой
Введем
декартовы координаты, приняв центр шара
за начало координат. Плоскость xy
пересекает поверхность шара радиуса R
по окружности, которая задается
формулой
![]() Полуокружность,
расположенная над осью x, задается
уравнением
Полуокружность,
расположенная над осью x, задается
уравнением
![]() Поэтому
объем шара определяется по формуле
Поэтому
объем шара определяется по формуле
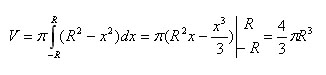
Шаровым
сектором называется
тело, которое получается из шарового
сегмента и конуса следующим образом.
Если шаровой сегмент меньше полушара,
то шаровой сегмент дополняется конусом,
у которого вершина в центре шара, а
основанием является основание сегмента.
Если же сегмент больше полушара, то
указанный конус из него удаляется. Объем
шарового сектора получается сложением
или вычитанием объемов соответствующих
сегмента и конуса. Для объема шарового
сектора получается следующая формула:
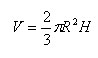 ,
где R – радиус
шара, а H – высота соответствующего
шарового сегмента..
,
где R – радиус
шара, а H – высота соответствующего
шарового сегмента..
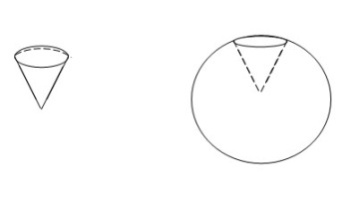
Шаровым
сегментом называется
часть шара, отсекаемая от него
плоскостью.
Формулу
для объема шарового сегмента получаем
аналогично формуле объема шара:
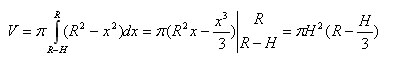 где
R – радиус шара, а H – высота шарового
сегмента.
где
R – радиус шара, а H – высота шарового
сегмента.
49. Критические точки функции. Теорема существования экстремумов функции.
Мы рассмотрели поведение функции на промежутках, где f(х)>0 и f'(х)<0. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 1 и 2). Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь французского математика Пьера Ферма).
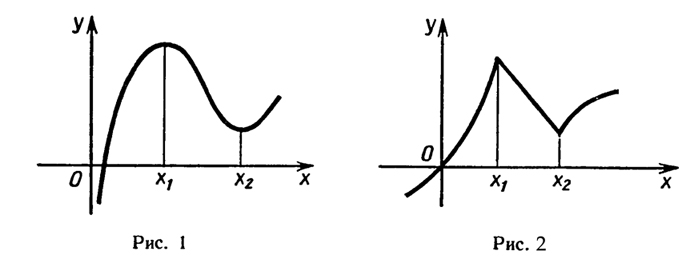
Необходимое
условие экстремума. Если точка хо
является точкой экстремума функции f и
в этой точке существует производная
f’, то она равна нулю:F’(x0)
=0.
Рассмотрим случай f'(x0)>0.
По определению производной отношение ![]() при
х→х0
стремится к положительному числу f'
(х0),
а следовательно, и само будет положительно
при всех х, достаточно близких к x0.
Для таких х
при
х→х0
стремится к положительному числу f'
(х0),
а следовательно, и само будет положительно
при всех х, достаточно близких к x0.
Для таких х
![]()
и, значит, f(x)>f(x0) для всех х>х0 из некоторой окрестности точки x0. Поэтому х0 не является точкой максимума. Если же х<х0, то f (x)<f(x0), и, следовательно, х0 не может быть и точкой минимума f. Случай F'(x0)<0 разбирается аналогично.
Важно
отметить, что теорема Ферма есть лишь
необходимое условие экстремума: из
того, что производная в точке хо обращается
в нуль, необязательно следует, что в
этой точке функция имеет экстремум.
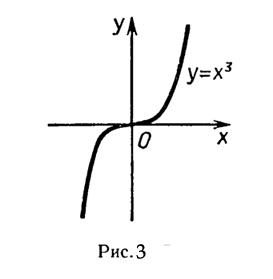
Например, производная функции
f(х)=х3 обращается
в нуль в точке 0, но экстремума в этой
точке функция не имеет (рис. 3).
До
сих пор мы рассматривали критические
точки, в которых производная равна нулю.
Рассмотрим теперь критические точки,
в которых производная не существует.
(Отметим, что, например, точка 0 для
функции ![]() не
является критической: в ней производная
не существует, но она не внутренняя
точка области определения.) В этих точках
функция также может иметь или не иметь
экстремум.
не
является критической: в ней производная
не существует, но она не внутренняя
точка области определения.) В этих точках
функция также может иметь или не иметь
экстремум.
