62. Шар. Сфера. Уравнение сферы.

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром.

(x − x₀)² + (y − y₀)² + (z − z₀)² = R², где (x₀,y₀,z₀) — координаты центра сферы, R — её радиус

63. Сечения сферы, шара плоскостью. Плоскость, касательная к сфере.

Всякое сечение шара плоскостью есть круг. Центр этого круга – основание перпендикуляра, опущенного из центра шара на секущую плоскость.

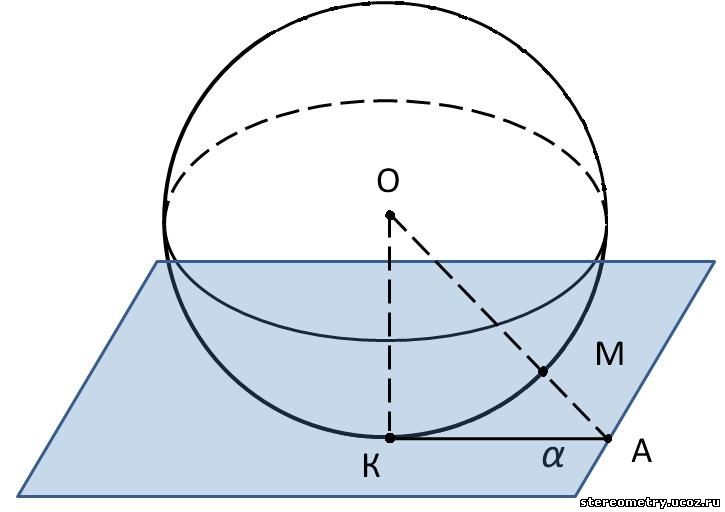
Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

64. Понятие объема тела. Общие свойства объемов многогранников.

Для простых тел, т.е. если его можно разбить на конечное число треугольных пирамид, - это положительная величина, которая обладает следующими свойствами:

• Равные тела имеют равные объемы

• Если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей.

• Объем куба, ребро которого равно единице длины, равен единице

65. Объем прямоугольного параллелепипеда. Объем произвольной призмы (вывод).

Объем прямоугольного параллелепипеда с линейными размерами a, b, c вычисляется по формуле V =abc

Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен

V_k = S_k • H

где S_k — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:

66. Объем пирамиды (вывод). Объем усеченной пирамиды.

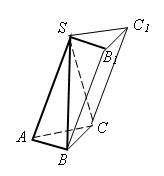
Пусть SABC – треугольная пирамида с вершиной S и основанием ABC. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма составлена из трех пирамид: данной пирамиды SABC и еще двух треугольных пирамид SCC₁B₁ и SCBB₁.  У второй и третьей пирамид равные основания - ΔCC₁B₁ и ΔB₁BC и общая высота, проведенная из вершины S. Поэтому у них равные объемы.  У первой и третьей пирамид тоже равные основания - ΔSAB и ΔBB₁S и совпадающие высоты, проведенные из вершины C. Поэтому у них тоже равные объемы.  Значит, все три пирамиды имеют один и тот же объем. Так как сумма объемов равна объему призмы, то объемы пирамид равны 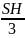.  Объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:   

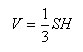
Есть усеченная пирамида с площадями оснований S1 и S2 (S1>S2) и высотой h. 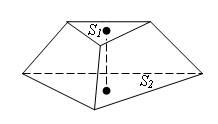   Тогда объем усеченной пирамиды равен: