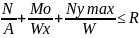29. Проверочный и проектировачный расчет

При проверочном расчете когда площадь поперечного сечения задана проверочным условием прочности следующим образом:

1. Оределяем минимальный радиус инерции

2. Определяем гибкость стойки (λ=μ*l\i min)

3. По гибкости и материалу стержня определяют коэффициент (фи)

4. Определяется расчетное сопротивление на устойчивость (формула)

5 Проверяется устойчивость δ=F\A≤Ry

При проектировачном расчете площадь сечения и коэффициент продольного изгиба, неизвестные. Для подбора поперечного сечения одной из величин необходимо задаться. Обычно задаются (фи):

y-это фи !!!!!!!!!!!!!!!!!!!!!!

1 y=0.5

2 δ=F\A≤y*R Aтр≥F\yR

3 I min= Imin\A (под корнем)

4 λ=μl\i min

5 λ―y

6 δ=F\A≤R*y=Ry

7 сравниваются δ и F

Если расхождения не превышают 5 %, то расчет заканчивается, в противном случае задается новое значение (фи).

y2=(y+y1)\2

Рациональные формы сечений сжатых стержней.

Желательно чтобы сечение имело возможно больший минимальный момент инерции при возможно меньшей площади сечения. Этому условию удовлетворяет трубчатое сечение.

Наиболее экономичное сечение у которого Ix=Iy. Такие сечения называются равноустойчивыми.

I min<<I max

Из нескольких продольных профилей можно составить рациональные формы сечения.

30. Проверочный и проектировочный расчеты на устойчивость

При проверочном расчете, когда площадь поперечного сечения задана, проверяют условие устойчивости след.образом:

1)определяют минимальный радиус инерции i_min=

2)определяют гибкость стойки λ=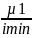

3)по гибкости и материалу стержня определяют коэф-т φ; λ → φ 4)определяется расчетное сопротивление на устойчивость Ry=R*φ 5)проверяется устойчивость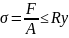 При проектировочном расчете площадь сечения и коэфф-ент продольного изгиба не известны. Для подбора поперечного сечения одной из величин необходимо задаваться. Обычно φ: 1)принимаем φ=0,5 2)определяем требуемую площадь поперечного сечения т.е. 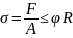;A ≥

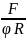
3)i_min= 4) λ = 5) λ → φ6) провер. условие устойчивости

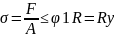
7) сравниваем 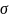и R. Если расхождение не превышает 5%,то расчет заканчивается,в противном случае задается новое значение 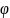. 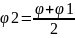, и далее расчет повторяется.

31. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Если к стержню одновременно приложены продольная сила Nи поперечная нагрузки, то возникает продольно-поперечный изгиб.

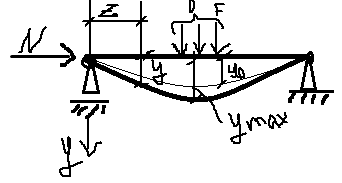
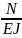Изгибающий момент в сечении на расстоянии z можно рассматривать как сумму двух моментов. М= - (М_о+ N_у), где Мо- изгибающий момент от поперечных нагрузок, Ny-изгибающий момент от продольной силы. Запишем диф-ое уравнение изогнутой оси балки EJy”=M EJy”=-(Mo+Ny) * ----------------------- EJy”+Ny=-Mo y”+ y= -

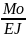
=K² y”+K²y=-

Решение этого уравнения представляет собой сумму 2 интегралов: интегр. однородного уравнения и частного интеграла неоднород. уравнения. Такая задача имеет сложное решение. Поэтому использ. приближ. метод решения т.е. задается деформация балки или стойки,но таким образом чтобы удовлетвор-сь граничные условия. При продольном изгибе было установлено,что балка изгибается по синусоидальному закону. Предположим,что и заданная балка деф-ся по такому же закону. y=y_maxsin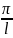 z; Проверим выполнение граничных условий. z=0 →y=0 z=1 →y=0 z=1/2 →y= y_maxпродиференцир. 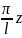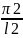заданное выражение * y’= y_max cos y”= - y_max sin zподставим значение 2-ой производной в выр-ие * EJy_max sin z=Mo+Ny

приz=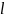 /2 y=EJy_max = Mo+Ny_{max обозначение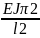} =Fэ – Эйлеровасила

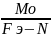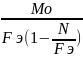здесь µ=1 Fэ= y_max-Ny_max=Мо y_max= y_max= y_max-полный прогиб от совместного действия поперечных и продольных сил. Зная максим.прогиб и внутр. силы запишем условия прочности.

σ_max= + =
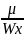