
- •1.Полная проверка прочности балки при изгибе.
- •2. Деформации при изгибе.
- •3. Определение перемещений методом непосредственного интегрирования диф-ого уравнения.
- •5. Начальные параметры в обобщенном уравнении изогнутой оси балки, их определение.
- •7. Универсальный метод определения перемещений (интеграл Мора).
- •8. Порядок определения перемещение с помощью интеграла Мора.
- •9. Теорема о взаимности работ и взаимности перемещений
- •10.Графоаналитеческий способ решения интеграла Мора (способ Верещагина)
- •11) Статически неопределимые системы.Метод расчета. Основная и эквивалентная система.
- •12) Основы метода сил.
- •13.Расчёт неразрезных балок методом сил. Порядок расчёта.
- •14. Косой изгиб. Определение. Внутренние силы. Напряжение.
- •15 Расчёт на прочность при косом изгибе.
- •16 Определение деформаций при косом изгибе
- •17 Растяжение-сжатие с изгибом. Внутренние силы. Напряжение.
- •18) Нецентренное растяж,сжатие
- •19. Расчет на прочность при внецентренном растяжении ( сжатии).
- •20 Ядро сечения
- •21. Изгиб с кручением. Определение. Внутренние силы. Напряжение
- •22. Расчет на прочность при изгибе с кручением
- •23. Общий случай сложного сопротивления (пространственный стержень)
- •24 Понятие устойчивости и критической силы
- •25 Формула Эйлера для определения критической силы
- •26 Выражение Эйлера при различных закреплениях концов стержня.
- •27) Гибкость стержня. Критическое напряжение.
- •28. Расчет на устойчивость
- •29. Проверочный и проектировачный расчет
- •30. Проверочный и проектировочный расчеты на устойчивость
- •32. Динамические нагрузки.Определение.Учет сил инерции
- •33. Удар. Определение. Основные допущения принятые в теории удара.
- •34. Определение динамического коэфф. При ударе.
- •35.Продолный удар.
- •36.Поперечный удар
- •37. Испытание материалов на удар (ударная проба).
- •38. Понятие усталостного разрушения при переменном напряжении.
- •39. Виды циклов напряжений при переменных напряжениях.
- •40. Кривая усталости. Предел выносливости.
- •41. Влияние различных факторов на предел выносливости.
1.Полная проверка прочности балки при изгибе.
Как показал опыт эксплуатации изгибаемых элементов конструкций, разрушение их начинается с крайних волокон, где возникают наибольшие норм.напряжения
Вычисляем главное напряж. для целого ряда точек по высоте сечения можно построить эпюры δ1 и δ3 . Зачастую скачки на эпюрах δ1 δ 3 превышают δ max.Поэтому возник.необходимость полной проверки прочности балки
По нормальным напряжениям в сечении где возникает наиб.изгибающий момент: δ
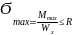
По касат. напряжению в сечении где возникает наибольшая поперечная сила:
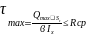
По главным напряжениям в точке примыкания полки к стенке(т.А) в сечении, где одновременно возникают наиб. изгибающий момент и поперечная сила. Проверка в опасной т.Аосуществл. по одной из теорий прочности. Сначала в этой точке определ. главныенапряж. по ф-ле:
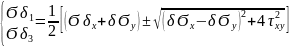
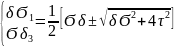
Подставляем главное напряжение в условие прочности по теории наиб.касат. напряжений:
δ1
-
δ3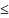 R
R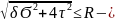 3-я теория прочности или теор. наиб касат
напряжений
3-я теория прочности или теор. наиб касат
напряжений
Аналогично условие прочности по теории энергоформы изменения примет вид:
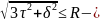 4-я
теор. прочности
4-я
теор. прочности
2. Деформации при изгибе.
При действии нагрузок балка деформируется, а её ось искривляется. Изогнутую ось балки можно характеризовать двумя параметрами: 1) прогибом y; 2) углом поворота сечения θ. (Рисунок 1)
Прогибом балки в данном сечении наз. перемещение центра тяжести сечения в направлении перпендик. оси балки.
Углом поворота сечения наз. угол поворота поперечного сечения к своему первоначальному положению.
Изогнутая ось балки наз. упругой линией.
Определение перемещений у и θ необходимы для расчёта элемента на жёсткость. Условие жёсткости требует что бы максимальный прогиб и угол поворота не превышали допускаемых значений
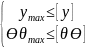 – условие
жёсткости.
– условие
жёсткости.
Допускаемый
прогиб устанавливается нормами
проектирования в зависимости от
назначения конструкции. Для балок это
обычно
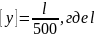 -
длина пролёта.
-
длина пролёта.
Приближённое дифференциальное уравнение изогнутой оси балки.
Рассмотрим балку нагруженную силой F. (рисунок 2)
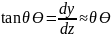
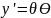 – первая
производная от прогиба равна углу
поворота сечения
– первая
производная от прогиба равна углу
поворота сечения
Ранее
была установлена зависимость
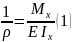 ;
из высшей математики известно
;
из высшей математики известно
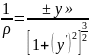 , т.к.
, т.к.
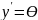 – величина малая, ей можно пренебречь,
получим
– величина малая, ей можно пренебречь,
получим
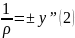
Приравниваем
правые части ур-ий (1) и(2)
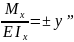
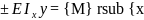 -
приближённое
дифференциальное ур-е изогнутой оси
балки.
-
приближённое
дифференциальное ур-е изогнутой оси
балки.
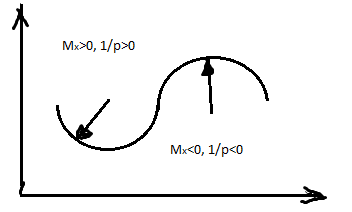
Знаки кривизны и изгибающего момента совпадают если изогнутую ось поместить в 1-ом квадранте координатных осей т.е. начало координат выбирать в центре тяжести крайнего левого сечения балки, ось ординат направлять вверх, ось абсцисс совмещать с осью прямой балки :Mx>0, 1/p>0; Mx<0, 1/p<0.
 С
учётом этого диф. ур-е в дальнейшем будет
записываться со знаком +.
С
учётом этого диф. ур-е в дальнейшем будет
записываться со знаком +.
3. Определение перемещений методом непосредственного интегрирования диф-ого уравнения.
Для определения θ и y проинтегрируем диф-оеуравнене
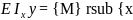 ;
;
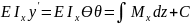 ;
;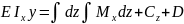 ;
;
C иD – постоянные интегрирования, определ. из граничных условий закрепления балки.
Для консольной балки найти ymaxи θ max
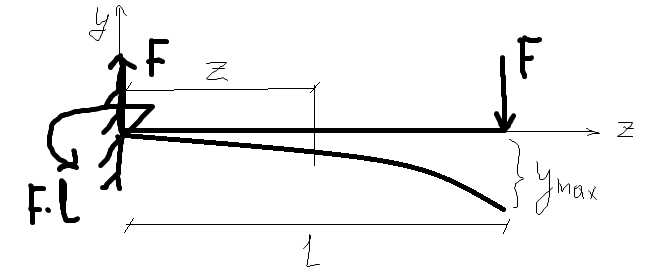
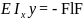
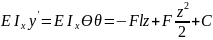
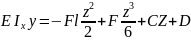
Определим постоянные интегрированияC иD
ПриZ=0 (защимление):y0=0, θ0=0
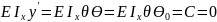
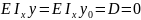
Найдём ymaxи θ max при z=l
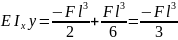
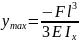
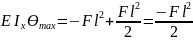
Знак «-» угла поворота указывает что сечение повернулось по часовой стрелке, а знак «-» у прогиба означает что прогиб произошёл вниз.
4.Обобщенноеур-е изогнутой оси балки. Метод начальных параметров. Для балок, имеющих 1 участок интегрирования, применение диф-го ур-я не вызывает затруднений. При большом кол-ве участков возникает много постоянных интегрирования Си D, поэтому в этом случае составляются диф-ные ур-я не для каждого участка, а одно обобщенное, соблюдая при этом некоторые условия и приёмы интегрирования: 1) В начало координат помещается крайнее левое сечение балки.
2) Изгибающий момент составляется от сил, расположенных левее исследуемого сечения.
3)При наличии сосредоточенного момента на балке изгибающий момент от него записывается в виде:
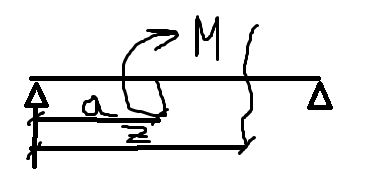
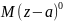
4)
Если распред. Нагрузка не доходит до
рассм. Сечения, то её необходимо продлить
до сечения и приложить уравновешивающую
нагрузку.
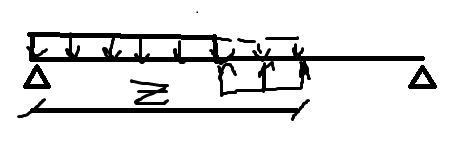
5) Интегрирование обобщенного ур-я производится без раскрытия скобок.
Рассм. Загруженную балку (рисунок!):
Под
действием нагрузок балка деформируется
и в начале координат прогиб будет
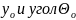 .Запишем
приближенное диф-ноеур-е для ряда
участков.При записи ур-й использ. Правило
знаков как для изгибающего момента.
.Запишем
приближенное диф-ноеур-е для ряда
участков.При записи ур-й использ. Правило
знаков как для изгибающего момента.
1
уч.
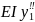 =0;
EI
=0;
EI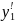 =
=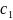 ;
EIy=
;
EIy=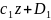
2
уч.EI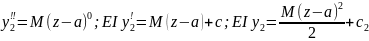 z
+
z
+
5
уч.
EI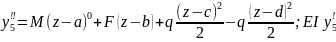 =M(z-a)+
=M(z-a)+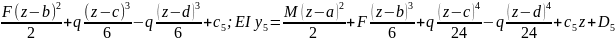
На
смежных участках углы поворота и прогибы
одинаковы.
При z=a;
=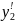 ;
;
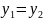
Из
выражений углов поворота и прогибов
следует:
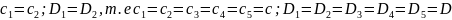 .
Для выяснения физической сущности
постоянных интегрирования С и Dрассм.
1 уч.:
При z=0;
.
Для выяснения физической сущности
постоянных интегрирования С и Dрассм.
1 уч.:
При z=0;
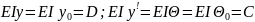 .
Вывод:Постоянные
интегрирования С и D
представляют собой угол поворота и
прогиб в начале координат,умноженные
на жесткость балки.
Можно записать
обобщенное ур-е изогнутой оси
балки.
.
Вывод:Постоянные
интегрирования С и D
представляют собой угол поворота и
прогиб в начале координат,умноженные
на жесткость балки.
Можно записать
обобщенное ур-е изогнутой оси
балки.
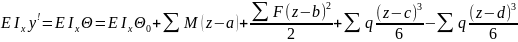 ;E
;E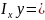 E
E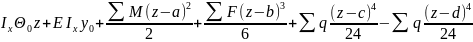 .В
этих ур-х нач. параметры E
.В
этих ур-х нач. параметры E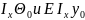 неизвестны. Их необходимо определить.
Поэтому этот метод получил название-метод
начальных параметров.
неизвестны. Их необходимо определить.
Поэтому этот метод получил название-метод
начальных параметров.
