1 Граф и его подграфы

Неориентированный граф без петель и кратных ребер называется обыкновенным графом.

Пусть -- конечный обыкновенный граф с множеством вершин 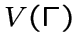и множеством ребер .

Подграфом графа называется граф такой, что его множество вершин 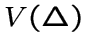является подмножеством множества вершин из , а его множество ребер является подмножеством множества ребер из .
Подграф, у которого вершины смежны тогда и только тогда, когда они смежны в , называется порожденным подграфом.
Множество всех порожденных подграфов графа обозначим через .

Поскольку в диссертации не рассматриваются подграфы, которые не являются порожденными, то подграфом называется только порожденный подграф.

Сокращяя обозначения, используем для множества вершин и для подграфа один и тот же символ .

Пусть 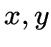вершины графа . Последовательность вершин называется путем в графе , если является ребром для всех .
Расстоянием между вершинами графа называется наименьшая длина пути, соединяющего вершины в . Пусть -- расстояние между вершинами графа . Положим 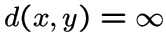, если вершины принадлежат различным связным компонентам графа .
Удаленностью вершины в называется наибольшее расстояние , где пробегает все множество вершин из .
Радиусом графа называется наименьшая из удаленностей его вершин.
Кликой называется полный подграф.
Граф , у которого вершины смежны тогда и только тогда, когда они не смежны в называется дополнительным.

К названиям понятий, соответствующих дополнительному графу, добавляют приставку "ко".

Кокликой называется вполне несвязный подграф.
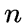-угольником 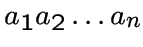называется связный регулярный граф валентности два на вершинах, в котором , -- ребра, .
Через 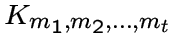обозначим полный многодольный граф с долями порядков 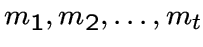. Если -- подмножества вершин полного многодольного графа , соответствующие его долям, то для используем обозначение .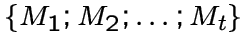
Если 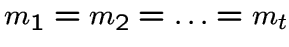, то обозначается через .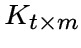
Граф называется 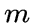-лапой, если .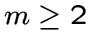
Граф 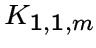называется -короной, если .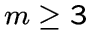
Для вершины 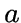графа через обозначается подграф на множестве всех вершин, которые находятся на расстоянии 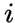от вершины . Подграф называется -той окрестностью вершины в графе .
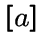Через обозначается . Если граф зафиксирован, то обозначается через . Этот подграф называетсяокрестностью вершины в .
Множество всех окрестностей графа обозначим через .
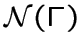Подграф на множестве 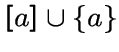обозначим через . Подграф называется замкнутой окрестностью вершины графа .
Для подграфа из и вершины из обозначим через окрестность в , а через . Если не принадлежит , то через обозначим пересечение окрестности в с .
Подграф на множестве обозначается через . Этот подграф называется антиокрестностью вершины в .
Множество всех антиокрестностей графа обозначим через .
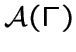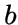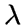Если и -- смежные вершины графа , то подграф на множестве всех вершин, которые смежны с ними обеими, называется -подграфом для 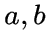и обозначается через или просто .
Множество всех -подграфов графа обозначим через .
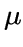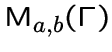Если и -- несмежные вершины графа и расстояние между ними в равно 2, то подграф на множестве всех вершин, которые смежны с ними обеими, называется -подграфом для и обозначается через или просто .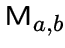
Множество всех -подграфов графа обозначим через .
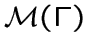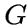Графом Тервиллигера называется неполный граф, в котором для любого подграф является кликой из вершин для некоторого фиксированного 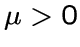.