§6. Анализ модели Уилсона на чувствительность.

На практике часто возникает ситуация, когда оптимальный размер партии поставки невыгодно или невозможно перевозить из-за отсутствия соответствующего транспорта или по другим техническим причинам. Возникает вопрос, если отклоняться от оптимального размера партии поставки, насколько изменятся издержки. Поэтому исследуем модель Уилсона с целью, какое влияние оказывают отклонения от оптимального размера партии поставки на общие издержки.

Обозначим через q принятый в данной организации размер партии поставки, а через q^* – оптимальный размер партии поставки. Пусть δ – отношение q на q^*, т.е.:

.

Найдём отношение издержек .

Воспользуемся формулами (1) и (3) из §4 и подставим в это отношение, имеем:

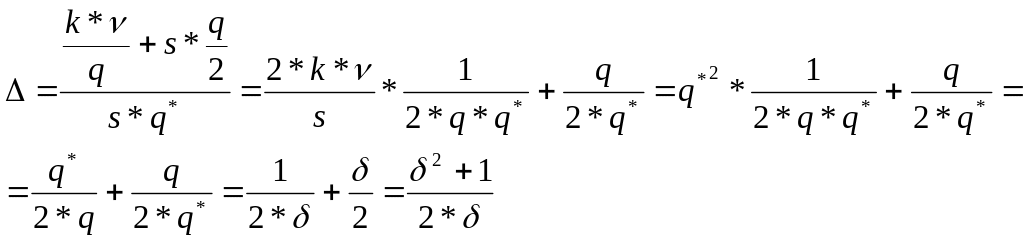
(1) Эта формула не зависит от параметров системы. График выглядит так:

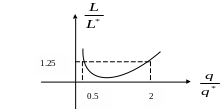
Полученная формула показывает, что небольшие отклонения партии поставки от оптимального значения не очень сказываются на издержках функционирования системы. Например, если увеличить размер партии поставки в 1.5 раза, т.е. , то издержки увеличатся всего на 1.083 раза; если , т.е. в два раза, тогда раза. Для того чтобы издержки увеличились в два раза, необходимо увеличить размер партии поставки почти в 3.73 раза.

При всех значениях δ , т.е. при отклонении размера партии поставки от оптимального значения издержки увеличиваются. В рассмотренном случае, если δ=1.5, то , т.е., если фактические размеры партии поставки установлены на уровне 150% к оптимальному размеру, то это вызывает повышение издержек по управлению всего на 8.3%, если δ=0.5, т.е., если размеры партии поставки уменьшить в два раза относительно оптимального размера, то всё равно издержки управления увеличиваются в 1.25 раз, т.е. на 25%.

Такая слабая чувствительность модели позволяет управлению запасами регулировать размер партии поставки с транспортными возможностями.

Аналогичная ситуация и при изменении других параметров модели. Например, рассмотрим влияние относительной погрешности в исчислении параметра s на издержки системы. Пусть:

,

тогда:

.

Из этой формулы следует, что, если издержки на хранение единицы запаса увеличить в 1.5 раза, то это приведёт к расширению суммарных издержек управления запасами на 2%.

Аналогично меняются суммарные издержки и при изменении параметра k , т.е., если

, то .

Это легко видеть, если в (1) положить .

Проведённый анализ чувствительности простейшей модели поставки приводит к выводу о правомерности применения упрощённых моделей. Кроме того, нет необходимости получать в отдельности численные значения издержек по завозу партии продукции и хранению единицы запаса, т.к. отношение между этими издержками равно .

18