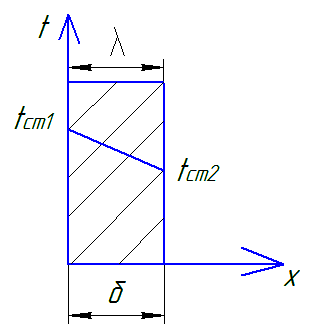
40. Теплопроводность плоской стенки (однослойной).

Рассмотрим однородную изотропную стенку толщиной с коэффициентом теплопроводности .

Примем, что и перенос тепла теплопроводностью осуществляется только в направлении оси Х, тогда уравнение Лапласа примет вид:

Граничные условия будут иметь вид:

: ; :

Проинтегрировав, получим:

(уравнение Лапласа).

Из полученного уравнения что изменение температуры в стенке будет происходить по линейному закону.

Постоянные интегрирования и находим из начальных условий:

,

Тогда отсюда получим:

Продифференцировав:

Подставив полученный градиент температуры в уравнение Фурье:

или

При установившемся режиме уравнение будет иметь вид:

- уравнение теплопроводности плоской стенки при установившемся режиме.

На практике дело приходится иметь с многослойными стенками.

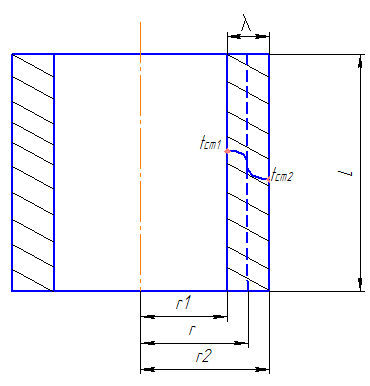
41. Теплопроводность цилиндрической стенки (одно- и многослойной)

- логарифмированная кривая.

r1 – внутренний радиус

r2 – текущий радиус

r3 – наружный радиус

Поскольку для цилиндрических стенок поверхность внутренней и наружной различны, то и использовать уравнение полученное для плоской стенки нельзя.

Для r поверхность теплопередачи будет:

Тогда уравнение Фурье:

Разделяя переменные уравнение Фурье будет иметь вид:

Проинтегрируем:

Для многослойной стенки:

При отношении можно использовать уравнение теплопроводности для плоской стенки.

Плоская многослойная стенка

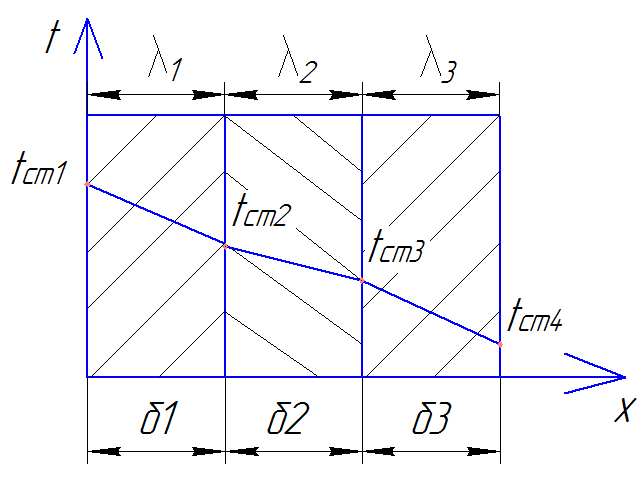
При установившемся режиме передачи тепла тепловой поток, который проходит через 1-ый слой, будет:

- для 1-го слоя

- для 2-го слоя

- для n-го слоя

или

Сложим левые и правые части уравнений:

- термич. сопротивление слоя; - терм. сопротивление многослойной стенки

42. Передача тепла конвекцией. Уравнение теплоотдачи.

Конвективный теплообмен происходит при движущейся среде, причем с ростом турбулентности потока передача тепла увеличивается. В ядре потока перенос тепла осуществляется одновременно и конвекцией и теплопроводностью. При этом, за счет турбулентных пульсаций, разность температур в ядре уравнивается до некоторой средней температуры. Интенсивность переноса тепла за счет конвекции падает, т.е. возле стенки создаётся пограничный ламинарный подслой, а там перенос тепла осуществляется только за счет теплопроводности.

Плотность теплового потока в направлении оси х по аналогии с теплопроводностью запишется:

- коэффициент турбулентной теплопроводности, не зависит от физических особенностей теплоносителя, а обусловлен турбулентностью потока поля температур и другими факторами.

Интенсивность переноса тепла за счет конвективного теплообмена характеризуют коэффициентом турбулентной температуропроводности :

Понятно, что на стенке теплоносителя =0, и увеличивается по мере приближения к ядру потока. В ядре потока принимают, что .

Приведенная на картинке схема переноса тепла, иллюстрирует механизм переноса тепла очень приблизительно. Чтобы упростить расчеты по теплоотдаче используют закон Ньютона – Рихмана:

, где - коэффициент теплоотдачи

Если теплоноситель имеет температуру большую чем стенка, то закон примет вид:

Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и теплоносителем. Коэффициент теплоотдачи зависит от режима движения ж.(г) (Re), тепловых особенностей теплоносителя и геометрических параметров аппарата. Таким образом, чтобы рассчитать количество тепла, которое передаётся стенке (стенкой) необходимо знать .

В основном определяют из критериальных зависимостей, полученных на основе опытных данных, а исходной зависимостью для обобщения этих опытных данных является дифференциальное уравнение конвективного теплообмена.