Оглавление

оглавление 4

введение 5

Задача 1 6

Задача 2 12

задача 3 14

задача 4 18

БИблиографический список 22

Введение

Исследование операций, понимаемое как комплексная математическая дисциплина, занимающаяся построением, разработкой и применением математических моделей принятия оптимальных решений, является одним из наиболее интенсивно развивающихся разделов прикладной математики и имеет многочисленные приложения. В настоящее время методы исследования операций находят широкое применение в решении самых различных практических задач, начиная от перспективного планирования разработок и кончая прогнозированием развития сферы обслуживания. Это связано с тем, что любая операция представляет собой совокупность целенаправленных действий, а исследование операций – поиск путей достижения одной или нескольких целей.

Математическая дисциплина, непосредственно связанная с исследованием операций, занимающаяся изучением экстремальных задач и разработкой методов их решения, называется математическим программированием. В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции

(1)

при условиях

(2)

где f и y – заданные функции;

b_i – некоторые действительные числа.

Прежде всего задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции f и y линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача называется задачей нелинейного программирования.

В данной курсовой работе будут рассмотрены три задачи линейного программирования и одна задача нелинейного программирования и методы их решения. Среди задач линейного программирования будет рассмотрена одна специальная задача линейного программирования – транспортная задача.

Задача 1

Условия задачи 1 приведены на странице 4. Предположим, что яхт-клуб закупил x₁ судов первого типа (Катер KRS-15L), x₂ судов второго типа (Яхта YT-25L), x₃ судов третьего типа (Яхта YT-35S) и x₄ судов четвертого типа (Яхта YTM-50L).

Очевидно, что целью яхт-клуба является потратить как можно меньше средств на покупку яхт, поэтому целевой функцией является общая стоимость закупки. Данную целевую функцию необходимо минимизировать. Таким образом, целевая функция примет вид

(3)

Коэффициенты при переменных в функции (3) это цена на единицу из условия.

Составим систему ограничений, пользуясь условиями задачи

(4)

Запишем данную задачу в форме основной задачи линейного программирования (далее ОЗЛП). Для этого целевую функцию (3) помножим на -1, а неравенства системы (4) приведем к равенствам.

(5)

(6)

Для выбора метода решения данной задачи, определим число свободных переменных. Для этого из числа переменных (5) и (6) n вычтем число ограничений m.

(7)

Так как число k больше двух, данную задачу затруднительно решать методом геометрической интерпретации. Поэтому применим симплексный метод, который заключается в переборе опорных решений из множества допустимых решений до тех пор, пока не будет достигнуто оптимальное решение.

Основой этого метода является симплекс-таблица. В этой задаче и во всех последующих будет применяться одинаковая схема заполнения симлекс-таблицы, предложенная в [2, стр. 31].

Для заполнения таблицы необходимо систему уравнений (6) переписать в векторной форме [2, стр. 32].

(8)

где P_j ( ) – вектор-столбец, составленный из коэффициентов при переменной x_j системы (6);

P₀ – вектор-столбец, составленный их свободных членов системы (6).

Следуя этим рассуждениям, векторы P примут вид.

(9)

Составим опорное решение, которое определяется единичными векторами из множества (9), образующих, так называемый, базис m-мерного пространства. К сожалению, базис при данных условиях не собирается, так как в (9) всего три единичных вектора, когда необходимо m=5.

Два недостающих вектора добавим искусственно [2, стр. 49], для чего из (5) и (6) составим расширенную задачу.

(10)

Для достройки базиса искусственно созданные переменные x₉ и x₁₀ прибавим соответственно в равенства 5 и 4 системы (6).

(11)

Теперь к уже имеющимся векторам (9) добавятся два новых.

(12)

Расширенная задача при базисе P₅, P₆, P₇, P₉, P₁₀ имеет опорный план

. Далее попытаемся исключить из базиса искусственные вектора, а значит и искусственные переменные. Составим симплекс-таблицу (таблица 1).

Таблица 1

				-9104	-25104	-4105	-6104	0	0	0	0	-M	-M
i	Баз.	Сб	P0	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10
1	P5	0	300	0	6	0	16	1	0	0	0	0	0
2	P6	0	2000	50	90	150	210	0	1	0	0	0	0
3	P7	0	112	2	6	8	15	0	0	1	0	0	0
4	P10	-M	100	2	6	8	15	0	0	0	-1	0	1
5	P9	-M	20	1	1	1	1	0	0	0	0	1	0
6				9104	25104	4105	6104	0	0	0	0	0	0
7				-3	-7	-9	-16	0	0	0	1	0	0

Как она заполняется нетрудно понять. В первом столбце для удобства ведется нумерация строк. Второй столбец несет информацию о том, какие сейчас вектора базисные. Третий столбец заполняется коэффициентами при неизвестных, чьи вектора сейчас базисные, из целевой функции. Для таблицы 1 третий столбец заполняется из (10). Все последующие столбцы не что иное, как все имеющиеся вектора-столбцы P. Над каждым столбцом P для удобства выписывается коэффициент при соответствующей неизвестной в целевой функции. Для таблицы 1 это также функция (10).

Далее следует проверить, является ли план оптимальным. Согласно признаку оптимальности [2, стр. 33] план является оптимальным, если среди _j ( ) нет отрицательных. Если среди них есть хотя бы один отрицательный элемент, то есть возможность перейти к новому опорному плану.

Для отражения значения _j в симплекс-таблице существует строка 6 (в условиях искусственных переменных – 6 и 7). _j рассчитывается по формуле

(13)

где С_j – коэффициент при j-ой переменной из целевой функции.

Так для таблицы 1 _j рассчитываются так

(14)

Для удобства в строку 7 записывают, число, стоящее перед M, а все остальное в строку 6.

В условиях искусственных переменных анализируют 7 строку. Так как в ней есть отрицательные элементы, то данный опорный план не оптимален. Столбец, в котором стоит самое большое по модулю отрицательное значение является разрешающим (это столбец с вектором P₄). Далее исключим из базиса P₁₀ – это и будет разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент.

Перейдем к новой симплекс-таблице (таблица 2).

Таблица 2

				-9104	-25104	-4105	-6104	0	0	0	0	-M
i	Баз.	Сб	P0	P1	P2	P3	P4	P5	P6	P7	P8	P9
1	P5	0	580/3	-32/15	-2/5	-128/15	0	1	0	0	16/15	0
2	P6	0	600	22	6	38	0	0	1	0	14	0
3	P7	0	12	0	0	0	0	0	0	1	1	0
4	P4	-6104	20/3	2/15	2/5	8/15	1	0	0	0	-1/15	0
5	P9	-M	40/3	13/15	3/5	7/15	0	0	0	0	1/15	1
6				82000	226000	368000	0	0	0	0	4000	0
7				-13/15	-3/5	-7/15	0	0	0	0	-1/15	0

Разрешающий столбец в новой таблице становится единичным, причем единица появляется на месте разрешающего элемента. Также остаются неизменными все векторы, которые находятся в данный момент в базисе. В столбце базиса делается отметка о новом базисном векторе – это вектор разрешающего столбца. В столбце C_б ставится соответствующий коэффициент (тот, который стоит над новым базисным вектором). Все элементы разрешающей строки делятся на разрешающий элемент таблицы 1. Все остальные элементы заполняются по формуле трех точек.

Так заполним столбец вектора P₀ таблицы 2. Для получения первого элемента нужно взять три точки: значение, стоящее на этом же месте на предыдущей итерации (т.е. в таблице 1) – это число 300; элемент, стоящий в разрешающем столбце этой же строки на предыдущей итерации, – это число 16; число, стоящее в этом же столбце и в строке таблицы текущей итерации, номер которой совпадает с номером разрешающей строки предыдущей итерации, – это число 20/3. Далее из первого числа вычитают произведение двух последних. К примеру, столбец с вектором P₀ заполнится так

(15)

Аналогично заполняются все оставшиеся ячейки таблицы. Так как вектор P₁₀ исключен из базиса, и более использоваться не будет, нет смысла заполнять столбец, в котором он стоит.

Заполнив строки 6 и 7 по формуле (13), убеждаемся, что план не оптимален. Аналогичными рассуждениями выбираем разрешающий столбец (самый большой отрицательный элемент седьмой строки находится в столбце P₁). Исключаем второй искусственный вектор из базиса, т.е. разрешающей становится строка 5. Аналогичными рассуждениями переходим к новой симплекс-таблице (таблица 3). Столбец, в котором стоял P₉, также не заполняем.

Таблица 3

				-9104	-25104	-4105	-6104	0	0	0	0
i	Баз.	Сб	P0	P1	P2	P3	P4	P5	P6	P7	P8
1	P5	0	226,154	0	1,077	-7,385	0	1	0	0	1,231
2	P6	0	261,538	0	-9,231	26,154	0	0	1	0	12,308
3	P7	0	12	0	0	0	0	0	0	1	1
4	P4	-6104	4,615	0	0,308	0,462	1	0	0	0	-0,077
5	P1	-9104	15,385	1	0,692	0,538	0	0	0	0	0,077
6				0	1,7105	3,2105	0	0	0	0	-2,3103

Исключив из базиса искусственные векторы, мы фактически от расширенной задачи (10)-(11) вернулись к исходной (5)-(6). Из таблицы 3 опорное решение при базисных векторах P₅, P₆, P₇, P₄, P₁ имеет вид

. Заполнив строку 6 таблицы 3 по формуле (13), убеждаемся, что данный опорный план не является оптимальным, так как в строке есть отрицательный элемент. Следовательно, разрешающим становится столбец, в котором стоит вектор P₈. Для определения разрешающей строки будем последовательно находить значения отношения элементов вектора P₀ на ненулевые и неотрицательные элементы разрешающего столбца. Строка, в которой значение отношения будет минимальным, становится разрешающей.

(16)

Из (16) разрешающей становится строка 3 таблицы 3. Переходим к новой симплекс-таблице (таблица 4), исключив из базиса вектор P₇ и введя P₈.

Таблица 4

				-9104	-25104	-4105	-6104	0	0	0	0
i	Баз.	Сб	P0	P1	P2	P3	P4	P5	P6	P7	P8
1	P5	0	211,382	0	1,077	-7,385	0	1	0	-1,231	0
2	P6	0	113,842	0	-9,231	26,154	0	0	1	-12,31	0
3	P8	0	12	0	0	0	0	0	0	1	1
4	P4	-6104	5,539	0	0,308	0,462	1	0	0	0,077	0
5	P1	-9104	14,461	1	0,692	0,538	0	0	0	-0,077	0
6				0	1,7105	3,2105	0	0	0	2,31103	0

Заполнив строку 6 таблицы 4 по формуле (13), можно убедиться, что данное решение является оптимальным по признаку оптимального решения.

Из таблицы 4 оптимальное решение имеет вид

.

Из оптимального решения выпишем интересующие нас значения.

(17)

Целевая функция (3) при значениях переменных (17) примет вид

(18)

Неравенства (4) после подстановки примут вид

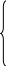
(19)

Полученное решение не противоречит системе ограничений.

Хотя и полученное решение нельзя назвать окончательным, так как количество яхт должно быть натуральным числом, в рамках линейного программирования задача считается решенной. Для получения конечного решения необходимо в дальнейшем обратиться к другому разделу математического программирования – целочисленное программирование.