
- •Введение
- •1Анализ алгоритмов методов
- •1.1 Метод lu-разложения
- •1.2 Метод Гаусса
- •1.3 Метод понижения порядка разложением по элементам строки
- •2Решение задач
- •2.1 Метод lu разложения
- •2.2 Метод Гаусса
- •2.3 Метод понижения порядка разложением по элементам строки
- •3Оценка решения задач заданными методами
- •4Оценка влияния погрешности исходных данных на погрешность результата
- •Библиографический список
2.1 Метод lu разложения
В предыдущем разделе была проанализирована применимость данного метода для каждой из исходных матриц. Напомним, что метод не применим только к матрице (3), поэтому ее предварительно необходимо преобразовать. Напомним, что сложение и вычитание любых столбцов и строк определителя на него не влияют. Если из второй строки матрицы (3) вычесть третью, то матрицу уже можно разложить на две треугольные.
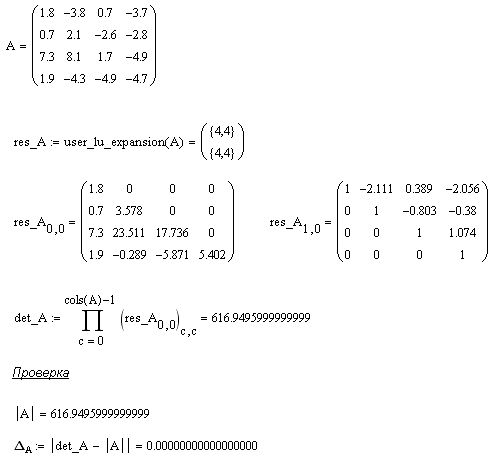
Представим результаты расчета в Mathcad и выполним проверку.
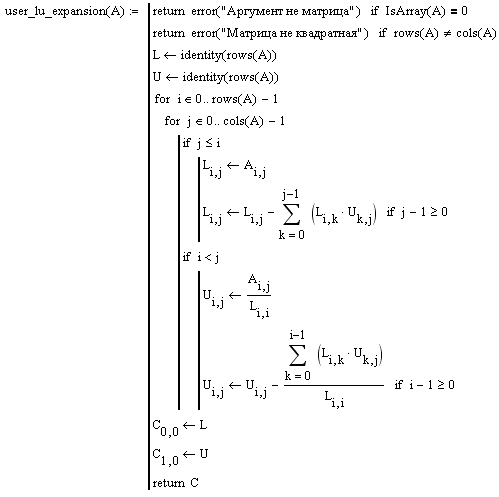
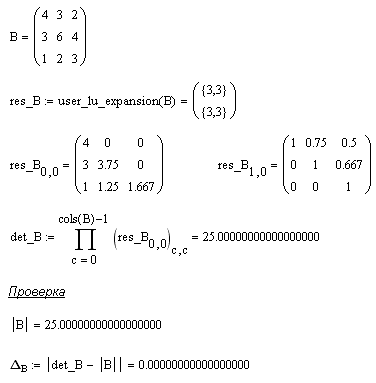
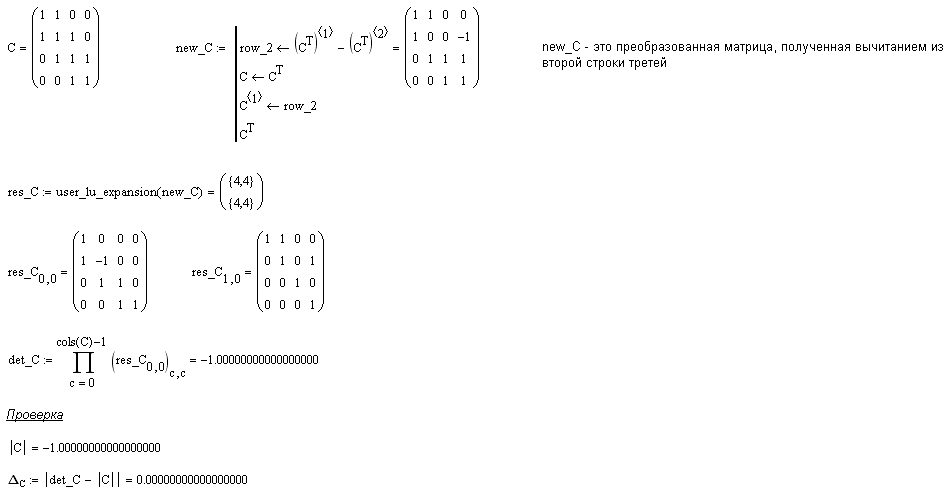
2.2 Метод Гаусса
Опять же было доказано, что метод применим ко всем исходным матрицам, кроме матрицы (3). Преобразование, проведенное в предыдущем методе над матрицей, так же позволяет найти определитель без лишних проблем.
Представим результаты расчета в Mathcad и выполним проверку.




2.3 Метод понижения порядка разложением по элементам строки
Представим результаты расчета в Mathcad и выполним проверку.

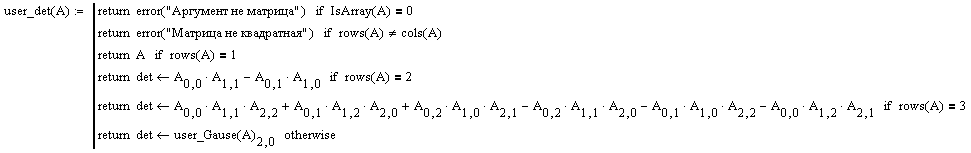


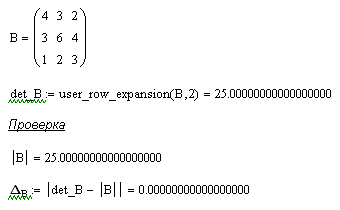

3Оценка решения задач заданными методами
Условимся, что результат, полученный внутренними алгоритмами Mathcad истинный. Очевидно, что определитель матрицы (1) это иррациональное число с периодом 9, начиная с пятого знака после запятой. Mathcad выводит этот результат с точностью до 13 знака после запятой включительно. Определители матриц (2) и (3) – это целые числа. Таким образом, мы видим расхождение только в методе Гаусса, где число было округлено до четвертого знака после запятой в определителе (1) внутренними алгоритмами оптимизации, а в определителе (2) появление неверной цифры в 15 знаке после запятой.
Чтобы сделать сравнение, сведем результаты в таблицу 1.
Таблица 1
Метод |
Определитель |
10-14 |
10-14,% |
LU-разложение |
(1) |
0 |
0 |
(2) |
0 |
0 |
|
(3) |
0 |
0 |
|
Метод Гаусса |
(1) |
11,37 |
1,8 |
(2) |
0,36 |
1,4 |
|
(3) |
0 |
0 |
|
По строке |
(1) |
0 |
0 |
(2) |
0 |
0 |
|
(3) |
0 |
0 |
|
|
|
|
|
На практике, как правило, таких высоких точностей не требуется и можно сказать, что все три метода дают верные результаты в пределах инженерной точности.
Дадим оценку приведенным методам. Самым универсальным оказался метод понижения порядка разложением по строке, потому что не имеет никаких ограничений, и применим к любому порядку. Однако метод становится очень громоздким для высших порядков, где нужно уже дробить алгебраические дополнения.
Самый простой алгоритм у метода LU-разложения, так как конечные выведенные формулы делают всегда предсказуемым результат. Единственный недостаток этого метода накладывает теорема о разложимости, поэтому всегда требуется предварительный анализ.
Метод Гаусса по универсальности стоит между методом LU-разложения и методом разложения по строке, так как тоже имеет ограничение.
Все три метода, рассмотренные здесь, являются «прямыми», а значит, погрешность результата появляется только из-за округлений в процессе решения. Это означает, что для уменьшения погрешности необходимо применять методологические рекомендации из арифметики по различным арифметическим операциям и операции округления.
