9 Центр линии второго порядка.

Определение 9.1. Центром линии второго порядка называется центр симметрии этой линии. ТЕОРЕМА 9.1. Пусть относительно аффинной системы координат задана линия второго порядка общим уравнением Для того чтобы начало координат являлось ее центром, необходимо и достаточно, чтобы в уравнении   отсутствовали члены с   и   в первой степени, т.е. чтобы  , иначе, чтобы уравнение линии имело вид Доказательство достаточности. Если  , то уравнение линии имеет вид   , и если ему удовлетворяют координаты   и   точки  , то ему удовлетворяют и координаты   и  точки  , симметричной точке   относительно начала координат. Доказательство необходимости. Пусть начало координат является центром линии  . Возьмем на линии произвольную точку  . Ее координаты удовлетворяют уравнению  , а так как начало координат является центром симметрии линии, то этому уравнению удовлетворят и координаты точки  , симметричной точке   относительно начала координат, т.е. . Вычитая из   соотношение  , находим, что координаты всех точек линии удовлетворяют уравнению  . Следовательно, уравнение линии приводится к виду  , то есть не содержит членов с   и   в первой степени. ТЕОРЕМА 9.2. Если относительно аффинной системы координат задана линия второго порядка общим уравнением то координаты   ее центра определяются из системы уравнений 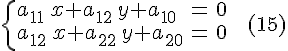причем в случае несовместности этой системы линия не имеет центра (т.е. является параболой). Доказательство. Произведем перенос данной системы координат так, чтобы новым началом стала точка  . В новой системе координат уравнение линии   будет иметь вид (согласно формулам  ). По предыдущей теореме точка   является центром данной линии тогда и только тогда, когда 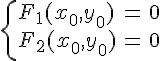или подробнее 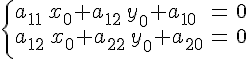Определение 9.2. Любая кривая второго порядка, имеющая единственный центр называется центральной. Следовательно, кривая является центральной, если Замечание 9.1. При приведении центральных кривых к каноническому виду целесообразно пользоваться следующим планом: 1. Найти центр кривой. 2. Выполнить параллельный перенос в центр и записать уравнение кривой в перенесенной системе координат 3. Повернуть перенесенную систему координат на угол   и получить каноническую систему координат.

10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка

Пусть задана кривая второго порядка общим уравнением и прямая   параметрическими уравнениями

.

Найдем точки пересечения этой прямой с кривой второго порядка. Для этого подставим значения переменных   и   из уравнений   в уравнение  . Получаем уравнение с одним неизвестным 

Преобразуем его к виду

Введем обозначения:

В этих обозначениях, полученное уравнение, запишется более просто, а именно

Находя корни уравнения  , и подставляя их в уравнения  , мы получим координаты точек пересечения кривой второго порядка и прямой  . При этом возможны следующие случаи: 1.  . Следовательно,   - квадратное уравнение, а поэтому оно имеет два корня (вещественных или комплексных),значит, прямая пересекает КВП в двух точках(вещественных или комплексно-сопряженных).

2.  . Тогда уравнение   примет вид  .

a). Если  , то прямая пересекает кривую в единственной действительной точке.

b). Если  , то прямая не имеет с кривой ни одной общей точки(ни действительной, ни мнимой).

c). Если  , тогда любое значение   является решением уравнения  , а потому   лежит на кривой второго порядка.

Определение 10.1. Множество всех прямых, из которых любые две параллельны, называется направлением.

Отметим, что направление можно определить любым направляющим вектором каждой из этих прямых. Заметим, что коэффициент в уравнении   зависит только от направления прямой   и не зависит от координат точки   , лежащей на прямой.

Определение 10.2. Направление, определяемое ненулевым вектором   , называется асимптотическим направлением относительно кривой второго порядка, если любая прямая, параллельная вектору   , либо имеет с кривой не более одной общей точки, либо содержится в кривой.

Из предыдущего следует: направление, определяемое ненулевым вектором  , является асимптотическим направлением относительно кривой второго порядка  , тогда и только тогда, когда

Пользуясь этой формулой, легко найти асимптотические направления относительно кривой второго порядка.

Если   , то из   следует, что   ( так как   -- ненулевой вектор), поэтому из  , обозначая через   получаем

Отсюда находим

Если же  , то уравнение   примет вид  . Этому уравнению удовлетворяют координаты векторов

Выясним теперь, сколько существует различных асимптотических направлений относительно кривой второго порядка. Рассмотрим три случая. 1.   и, значит,  . Из формулы   мы заключаем, что относительно кривой второго порядка не существует асимптотических направлений. 2.  . В этом случае существует два различных асимптотических направления. В самом деле, если   , то этот вывод следует из формулы  , а если   , то из  . (Заметим, что в последнем случае  , поэтому векторы из   не коллинеарны.) 3. . Очевидно, что в этом случае имеем единственное асимптотическое направление, определяемое вектором  . Действительно, если  , то это вытекает из  , а если  , то из  . (Заметим, что в последнем случае  , поэтому векторы из   коллинеарны.)

Ранее было показано, что   не зависит от выбора системы координат. В соответствии с таблицей значений инвариантов и количеством асимптотических направлений принято разделять кривые второго порядка на три класса: эллиптические  , гиперболические   и параболические  .

Определение 10.3. Асимптотой кривой второго порядка называется прямая асимптотического направления, которая либо лежит на кривой, либо не имеет с ней общих точек.

ТЕОРЕМА 10.1. Асимптота к кривой гиперболического типа задается уравнением

где   удовлетворяют  .

Доказательство. Запишем уравнение   в виде

или в эквивалентной форме

Отметим сначала, что это уравнение является уравнением первой степени. Действительно, предположим, что

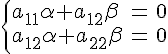
Откуда следует, что  , так как  . А это противоречит тому, что вектор, удовлетворяющий  , ненулевой. Теперь необходимо проверить, что прямая   имеет асимптотическое направление, т.е. надо убедится в том, что вектор   имеет асимптотическое направление. Действительно, так как   -- вектор асимптотического направления, то он удовлетворяют равенству

,

которое равносильно

Таким образом, вектор   коллинеарен вектору асимптотического направления, а значит, имеет асимптотическое направление. Итак, прямая, заданная уравнением   имеет асимптотическое направление. Кроме того, если точка лежит на этой прямой, то ее координаты   удовлетворяют уравнению  :

.

Рассмотрим выражение

Что и требовалось доказать. Замечание 10.1. Если в общем уравнении кривой второго порядка гиперболического типа  , то уравнения асимптот можно искать в виде

где   определяются по формуле  .