5 Стандартная схема упрощения уравнения кривой второго порядка.

Пусть относительно прямоугольной декартовой системы координат (ПДСК) дано общее уравнение кривой второго порядка (КВП)   , где  . Возникает естественный вопрос: Как по уравнению   определить с какой кривой мы имеем дело? Для ответа на этот вопрос упростим уравнение  , используя формулы преобразования декартовых систем координат, ориентированных одинаково. Любой такой перход можно осуществить в два этапа: поворот на некоторый оринтированный угол и последующий параллельный перенос повернутой системы. Рассмотрим каждый этап в отдельности. I) . Поворот. Возникают два случая. Если   , то ничего делать не надо и мы перейдем ко второму этапу. Пусть теперь  . Выполним поворот вокруг начала координат на угол  , который подберем так, чтобы исчезло слагаемое, содержащее  , т.е чтобы  . Это условие эквивалентно тому, что [см.  ]  или . Отсюда получаем, что необходимо выполнять поворот на угол, удовлетворяющий условию   Если мы выполняем поворот на угол, удовлетворяющий условию  , то в системе координат   данная кривая будет задаваться уравнением   , причем   и   не равны нулю одновременно. II). Параллельный перенос. Перенесем систему координат   в некоторую точку  , относительно системы координат  . В этом случае формулы параллельного переноса будут иметь вид Теперь подберем точку   так, чтобы максимально упростить уравнение  . Рассмотрим несколько случаев: 1.   и  . Подбираем точку  , чтобы в преобразованном уравнении исчезли слагаемые с переменными в первых степенях. Отсюда получаем, что  или   , то есть   и уравнение   принимает вид или с целью упрощения записи   2.  ,   и  В этом случае уравнение   принимает вид и мы подбираем точку  , чтобы в преобразованном уравнении исчезли слагаемые с переменной   в первой степени и свободный коэффициент. Это эквивалентно тому, что координаты точки   являются решением следующей системы 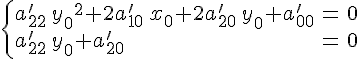. После такого выбора точки уравнение кривой примет вид  или   3.  ,   и  . Таким образом, имеем дело с уравнением вида и мы выбираем точку   так, чтобы в преобразованном уравнении исчезли слагаемые с переменной   в первой степени, то есть, чтобы   , а   — произвольное действительное число, например, . Получаем уравнение или проще   ВЫВОД. Если в системе координат   уравнение кривой имело вид  , то с помощью поворота и параллельного переноса системы координат его можно привести к одному из трех видов . Замечание 5.1. Случаи  ,   и   и  ,   и   сводятся к 2. и 3. соответственно, рассмотренным выше с помощью дополнительного поворота на угол  .

6 Полная классификация кривых второго порядка

Исследуем подробно каждое из полученных уравнений  I).  Возможны следующие случаи: 1.  . Уравнение   можно переписать в эквивалентной форме . a) Если   и  , то обозначая через   и   соответственно, получим уравнение  , которое определяет эллипс. b) Если   и  , то обозначая через   и   соответственно, получим уравнение  , которое определяет мнимый эллипс (этому уравнению не удовлетворяет ни одна вещественная точка плоскости). c) Если   и   или   и  , то обозначая через   и   или   и   соответственно, получим уравнение  , которое пределяет гиперболу. 2.   Тогда исходное уравнение принимает вид a) Числа   и   одного знака. Без ограничения общности можно считать, что они положительные (иначе обе части уравнения умножим на  ). Тогда обозначив через   и   , получим в этих обозначениях уравнение  , которое определяет две мнимые прямые, пересекающиеся в действительной точке  . b) Числа   и   - числа разных знаков. Будем считать, что   (иначе обе части уравнения умножим на  ). Тогда обозначив через   и   , получим в этих обозначениях уравнение   или , которое определяет две действительные пересекающиеся прямые. II).  . Запишем его в эквивалентном виде   . Обозначим  . В этих обозначениях получим уравнение  , которое определяет параболу. III).  . Перепишем его в виде   и рассмотрим возможные случаи : 1.  . a)   Тогда обозначим   и получим, что уравнение кривой приводится к виду  (или  ), которое определяет пару различных параллельных прямых. b)  . Тогда обозначим   и получим, что уравнение имеет вид  , которое определяет пару мнимых параллельных прямых. 2.  . Тогда уравнение принимает вид  , которое определяет пару совпавших прямых. ВЫВОД. Таким образом, имеется девять и только девять типов кривых второго порядка.