1 Формулы преобразования координат.

Задача преобразования координат состоит в следующем: Пусть на плоскости заданы две системы координат   — «старая» и   — «новая», а также произвольная точка плоскости   , имеющая координаты   и  соответственно. Требуется найти связь между старыми и новыми координатами точки  , зная координаты точки   и векторов   и   в старой системе координат. Рассмотрим на плоскости две аффинные системы координат   и  . Первую систему координат назовем старой, а вторую — новой. Пусть   — произвольная точка плоскости, которая в старой системе имеет координаты   , а в новой системе —  . Пусть  . По правилу треугольника  , поэтому имеем равенство  , или  . Учитывая, что векторы линейно независимы, приходим к формулам 

 

Это формулы преобразования аффинных координат. Заметим, что коэффициенты при переменных   составляют матрицу перехода от базиса   к базису   , поэтому   Следовательно, мы можем выразить координаты точки   в новой системе   через координаты той же точки в старой системе  . Не приводя эти формулы отметим только, что функции   и   линейные. Рассмотрим теперь преобразование прямоугольных систем координат. Возможны два случая. I. Обе системы   и   — ориентированы одинаково. Пусть  , а ориентированный угол между векторами   и   равен  . Найдем координаты векторов   в базисе  . Имеем   и  . Таким образом,  ;  . 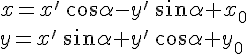Поэтому, формулы   принимают вид:     —   -- это формулы преобразования декартовых систем координат, ориентированных одинаково. II. Системы   и   — ориентированы противоположно. Пусть  , а ориентированный угол между векторами   и   равен  . Найдем координаты векторов   в базисе  . Имеем   и  . Таким образом,  ;  . В этом случае, формулы   принимают вид:       -- это формулы преобразования декартовых систем координат, ориентированных противоположно. Замечание 1.1. Формулы   и   можно записать вместе   где  . Замечание 1.2. Если  , то формулы   принимают вид     Формулы   — это формулы параллельного переноса. Замечание 1.3. Если  , то формулы   преобразования примут вид     Формулы   — это поворот системы координат вокруг начала координат на ориентированный угол  .

2 Алгебраические линии на плоскости.

Определение 2.1. Уравнением линией на плоскости называется множество решений уравнения  . При этом если   -— многочлен от двух переменных, то линия является алгебраической, а степень этого многочлена называется порядком линии. Таким образом, задать алгебраическую линию на плоскости — значит задать некоторое алгебраическое уравнение  и некоторую аффинную систему координат  ; тогда те и только те точки  , координаты которых в данной системе координат удовлетворяют этому уравнению, считаются лежащими на линии. Однако с определением линии не все обстоит так просто, как кажется на первый взгляд. Множество всех точек плоскости, удовлетворяющих уравнению  , совпадает с множеством точек, удовлетворяющих уравнению  . Однако мы будем считать, что это различные линии. Таким образом мы приходим к следующему соглашению: два уравнения тогда и только тогда определяют одну и ту же линию, когда одно из этих уравнений получается из другого почленным умножением на некоторый числовой множитель Если на плоскости дана система координат  , то левая часть уравнения   определяет функцию от точки плоскости: каждой точке  , имеющей в данной системе координат координаты  ,  , соответствует число  . Если мы перейдем к другой системе координат  , то эта же точка   , имевшая в системе   координаты   , получит в системе   новые координаты  , связанные со старыми координатами формулами преобразования координат (см. (1)). Для того чтобы вычислить значение того же числа   через новые координаты   точки   , надо в многочлен   вместо   подставить выражения (1) этих переменных через  ; от этого многочлен   тождественно преобразуется в выражение   от новых переменных  . Координаты   какой-либо точки   в системе  тогда и только тогда удовлетворяют уравнению  , когда координаты   той же точки в системе  удовлетворяют уравнению  . Справедлива следующая ТЕОРЕМА 2.1. Понятие алгебраической линии, а также порядок линии не зависит от выбора аффинной системы координат. Доказательство. Возьмем на плоскости аффинную систему координат  . Пусть в этой системе координат линия  определяется уравнением  , где   — многочлен степени  . Зададим на плоскости другую аффинную систему координат  . Координаты   произвольной точки   плоскости в системе   выражаются через ее координаты   в системе   по формулам (1). Чтобы получить уравнение линии   в системе  , надо в уравнении  заменить   их выражениями по формулам (1). Получим уравнение  . Поскольку   есть сумма членов вида  , то после замены получим, что   есть сумма членов вида , то есть снова многочлен от переменных   . Следовательно, понятие алгебраической линии не зависит от выбора аффинной системы координат. Докажем теперь, что   — многочлен степени   . Пусть   — степень этого многочлена. Если в выражении  раскрыть скобки и привести подобные слагаемые, то получим сумму членов вида  , где  . Отсюда следует, что  . Будем теперь считать, что   - старая система координат, а   — новая. Тогда по доказанному  . Итак,   и  , cледовательно  .