1 Эллипсоид.

Определение 1.1. Эллипсоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

Будем считать, что  . Из уравнения   следует, что если точка   лежит на эллипсоиде, то на нем лежат и точки  с любым набором знаков плюс и минус. Отсюда следует, что для эллипсоида   начало координат является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями. Если  , то эллипсоид называется трехосным. Если   (  ), то эллипсоид называется вытянутым (сжатым) эллипсоидом вращения. Каждый из них получается вращением эллипса вокруг большой (малой) его оси. Если  , то эллипсоид   является сферой радиуса   с центром в начале координат. Определение 1.2. Вершинами трехосного эллипсоида называются точки пересечения эллипсоида с его главными осями. Трехосный эллипсоид имеет шесть вершин  . Из уравнения   следует, что если точка   лежит на эллипсоиде, то ее координаты должны удовлетворять следующим условиям  . Это означает, что эллипсоид   лежит внутри прямоугольного параллелепипеда с вершинами  . Координатные плоскости   пересекают эллипсоид   по линиям, заданным уравнениями

Линии  ,  ,   --- эллипсы; эти эллипсы, т.е. сечения эллипсоида   его главными плоскостями, называются главными сечениями. Рассмотрим сечения эллипсоида   плоскостями, параллельными какой-нибудь координатной плоскости, например плоскостями, параллельными плоскости  , т.е плоскостями, заданными уравнением   , где   --- произвольное действительное число. Уравнения линий сечения будут или или Если  , то первому уравнения системы   не удовлетворяет ни одна пара действительных чисел  , то есть плоскость   при   не пересекает эллипсоид  . При   первое уравнение системы   имеет вид откуда  . Таким образом, плоскости   встречают эллипсоид   в его вершинах  . Наконец, если  , то систему   можно переписать в виде или Последние уравнения являются уравнениями эллипса, лежащего в плоскости сечения  ; центр этого эллипса --- точка  , оси симметрии параллельны осям   и  , а полуоси равны Рассмотренные сечения дают представление о форме эллипсоида.

2 Однополостный гиперболоид.

Определение 2.1. Однополостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

Будем считать, что  . Также как в предыдущем параграфе доказывается, что для однополостного гиперболоида   начало координат является его центром симметрии (центр); оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Если  , то однополостный гиперболоид   называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы вокруг ее мнимой оси. Определение 2.2. Вершинами однополостного гиперболоида называются точки пересечения однополостного гиперболоида с его главными осями. Однополостный гиперболоид   имеет четыре вершины  . Плоскость   пересекают однополостный гиперболоид   по эллипсу, заданному уравнениями

называемому горловым эллипсом однополостного гиперболоида  . Плоскость   пересекают однополостный гиперболоид   по гиперболе, заданной уравнениями

а плоскость   --- по гиперболе, заданной уравнениями

Линии  ,  ,   --- сечения гиперболоида   его главными плоскостями, называются главными сечениями. Рассмотрим сечения однополостного гиперболоида   плоскостями, параллельными координатной плоскости  , т.е. плоскостями, заданными уравнением   , где   --- произвольное действительное число. Уравнения линий сечения будут или или или Этими уравнениями выражается эллипс, лежащий в плоскости сечения  ; центр этого эллипса --- точка  , оси симметрии параллельны осям   и  , а полуоси равны Таким образом, горловой эллипс   является наименьшим из всех эллипсов, по которым однополостный гиперболоид  рассекается плоскостями, параллельными плоскости  . Плоскость  , параллельная координатной плоскости  , пересекает однополостный гиперболоид по линии, уравнения которой имеют вид или или Если  , то уравнениями   определяется гипербола, лежащая в плоскости сечения   с центром в точке  , действительная ось, которой параллельна оси  , а мнимая --- оси  . Полуоси этой гиперболы равны   --- действительная полуось и   --- мнимая полуось. При  , уравнения   принимают вид Уравнения являются уравнениями двух пересекающихся прямых   и  :  --- прямая   --- прямая  . Аналогично уравнения являются уравнениями двух пересекающихся прямых   и  :  --- прямая   --- прямая  . Если  , то уравнениями   определяется гипербола, лежащая в плоскости сечения   с центром в точке  , действительная ось, которой параллельна оси  , а мнимая --- оси  . Полуоси этой гиперболы равны   --- действительная полуось и   --- мнимая полуось. Сечения плоскостями  , параллельными плоскости  , рассматриваются аналогично. Все эти сечения дают представление о форме поверхности однополостного гиперболоида. 3 Двуполостный гиперболоид.

Определение 3.1. Двуполостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

Начало координат является его центром симметрии (центр); оси координат являются осями симметрии (главные оси); координатные плоскости являются плоскостями симметрии (главные плоскости). Если  , то двуполостный гиперболоид   называется двуполостным гиперболоидом вращения, так как может быть получен вращением гиперболы вокруг ее действительной оси  . Определение 3.2. Вершинами двуполостного гиперболоида называются точки пересечения двуполостного гиперболоида с его главными осями. Двуполостный гиперболоид имеет две вершины  . Плоскости   и   пересекают двуполостный гиперболоид   по гиперболам:

и

Плоскость   не пересекает двуполостный гиперболоид  . Линии  ,   --- сечения гиперболоида   его главными плоскостями, называются главными сечениями. Рассмотрим сечения двуполостного гиперболоида   плоскостями, параллельными координатной плоскости  , т.е. плоскостями, заданными уравнением  , где   --- произвольное действительное число. Уравнения линий сечения будут или или Если  , то первое уравнение   не имеет действительных решений, следовательно, в этом случае плоскость   не пересекает поверхность. При  , получаем откуда  . Таким образом, плоскости   встречают двуполостный гиперболоид   в его вершинах. Наконец, если  , то уравнения   сечения можно переписать в виде 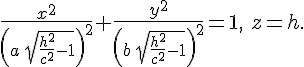Этими уравнениями задается эллипс, лежащий в плоскости сечения  ; центр этого эллипса --- точка  , оси симметрии параллельны осям   и  , а его полуоси равны которые увеличиваются по мере удаления секущей плоскости от плоскости  . Из рассмотрения данных сечений следует, что двуполостный гиперболоид состоит из двух частей, принадлежащих в различным полупространствам, относительно плоскости  . Плоскость  , параллельная координатной плоскости  , пересекает двуполостный гиперболоид   по линии, уравнения которой имеют вид или или или т. е. по гиперболе  лежащей в плоскости сечения   с центром в точке  , действительная ось, которой параллельна оси  ,а мнимая --- оси  . Аналогично исследуются сечения гиперболоида   плоскостями  . Все эти сечения дают представление о форме двуполостного гиперболоида.