Лекция 5. Нелинейные модели внешней торговли.
Часть 1. Модель р. Джонса
Учебные вопросы:
Производственные функции в нелинейных моделях вешней торговли.
Статическая нелинейная макроэкономическая модель, лежащая в основе модели Р.Джонса.
Построение модели Р. Джонса
Литература по теме:
Основная
Туманова Е.А., Шагас Н.Л. Макроэкономика. Элементы продвинутого подхода: Учебник. – М.: ИНФРА – М, 2006. – 400 с. – (Учебники экономического факультета МГУ им. М.В. Ломоносова).
Дополнительная
Воркуев Б.Л. Количественные методы исследования в микро- и макроэкономике. – М.: ТЕИС, 2010. – 436 с.
Введение
Теории международной торговли прошли в своем развитии ряд этапов вместе с развитием экономической мысли. Однако их главными вопросами были и остаются следующие: что лежит в основе международного разделения труда? Какая международная специализация является наиболее эффективной для стран? Количественные ответы на эти вопросы дают соответствующие модели.
На предыдущих лекциях мы рассмотрели простую модель внешней торговли и ряд ее обобщений. В этих моделях мы неявно полагали, что валовые объемы производства товаров являются линейными функциями затрат труда и капитала. Вместе с тем это условие выполняется только в достаточно малой окрестности точки, отражающей рациональную специализацию собственного производства и рациональное международное разделение труда.
В ходе настоящей и следующей лекций мы рассмотрим некоторые подходы, обеспечивающие снятие условия линейности в моделях внешней торговли. При этом целью настоящей лекции является рассмотрение модели Рональда Джонса. Эта модель позволяет при определенных предположениях определить наиболее эффективную специализацию экономики государства. Поскольку в модели Р. Джонса широко применяются производственные функции, то лекцию начнем с рассмотрения сущности и основных свойств производственных функций.
Производственные функции в нелинейных моделях вешней торговли
Инструментом анализа затрат на производство товаров при исследовании вешней торговли являются модели производственного процесса. В интересах моделирования производственный процесс следует определенным образом схематизировать и структурировать.
В обобщенном виде процесс производства экономических благ представляет собой преобразование имеющихся трудовых, капитальных и природных ресурсов в те или иные экономические блага. Это наглядно отражает рис. 5.1.1.
Рис 5.1.1. Обобщенная схема производства
Капитальные ресурсы в этой схеме отражают имеющиеся средства труда.
Формально процесс производства описывается производственной функцией . Производственная функция – это функция, независимая переменная которой принимает значения объемов используемого ресурса (фактора производства), а зависимая переменная – значения объемов выпускаемой продукции.
На рис 5.1. величине W соответствует вектор ().
Производственная функция представляет собой модель процесса производства.
В микроэкономике принято считать, что X - это максимально возможный объем выпуска продукции при затрате W ресурсов.
В макроэкономике это не так, поскольку величина X зависит от распределения имеющихся ресурсов между отраслями экономики. Поэтому в макроэкономике под производственной функцией понимают статистически устойчивую связь между затрачиваемыми ресурсами и производимыми экономическими благами.
Точное толкование понятий затрачиваемого ресурса и выпускаемых экономических благ, а, следовательно, и выбор единиц их измерения зависят от характера и масштаба производственной системы, а также от наличия исходных данных. На микроэкономическом уровне затраты и результаты могут измеряться как в стоимостных, так и в натуральных показателях.
На макроэкономическом уровне затраты ресурсов и результаты производства, как правило, измеряются в стоимостных показателях. При этом они представляются в виде соответствующих стоимостных агрегатов, формируемых как суммы произведений объемов ресурсов на их стоимости.
Производственная функция макроэкономической системы обычно представляется в виде
(5.1.1)
Или
(5.1.2)
Причем в виде (5.1.2) производственная функция на макроэкономическом уровне применяется наиболее часто.
Отсутствие в соотношении (5.1.2) природных ресурсов означает, что они не являются в рассматриваемой ситуации ограничивающим фактором для производства. Это допустимо при наличии достаточно больших природных ресурсов, превышающих потребности производства.
По экономическому смыслу производственная функция (5.1.2) должна удовлетворять условиям:
(5.1.3)
(5.1.4)
, (5.1.5)
, (5.1.6)
при K>0, L>0, , (5.1.7)
при K>0, L>0, , (5.1.8)
Свойства (5.1.3), (5.1.4) означают, что производственная функция является положительно определенной.
Свойство (5.1.5) означает, что без затрат ресурсов невозможно производство.
Свойство (5.1.6) означает, что капитал и живой труд не могут в полном объеме заменить друг друга в производственном процессе.
Свойства (5.1.7), (5.1.8) означают, что с ростом затрат хотя бы одного ресурса, при неизменном количестве другого объем производимых экономических благ растет.
Свойствам (5.1.3) – (5.1.8) удовлетворяют линейные производственные функции вида (5.1.2)
(5.1.9)
Вместе с тем такие функции не позволяют учитывать присущий процессу производства закон убывания эффективности. Необходимость его учета обусловила введение дополнительных свойств:
при K>0, L>0, (5.1.10)
при K>0, L>0, (5.1.11)
при K>0, L>0, (5.1.12)
. (5.1.13)
Свойство (5.1.10) означает, что с ростом затрат капитала при неизменном количестве живого труда величина прироста производства на каждую дополнительную единицу капитала не возрастает.
Свойство (5.1.11) означает, что с ростом затрат живого труда при неизменном количестве капитала величина прироста производства на каждую дополнительную единицу труда не возрастает.
Наглядно сущность этихсвойств иллюстрируют графики на рис. 5.1.2, 5.1.3.
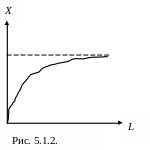
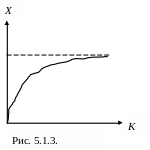
Указанные свойства (5.1.10) и (5.1.11) отражают фундаментальный экономический закон убывающей эффективности.
Свойство (5.1.12) означает, что при росте затрат одного ресурса, предельная эффективность другого возрастает. Тем самым оно учитывает взаимозависимость факторов производства в экономическом законе убывающей эффективности.
Свойство (5.1.13) означает, что эффективность производства зависит от изменения его масштаба. Так рост масштаба в λ –раз приводит к изменению объемов в λр раз.
При р=1 имеем независимость удельного выпуска экономических благ от масштаба производства. Производственные функции, для которых р=1, называют однородными первой степени. Именно это предположение и было нами принято при построении модели межотраслевого баланса.
Указанным свойствам (5.1.3) – (5.1.8), (5.1.10) – (5.1.13), в частности, удовлетворяет производственная функция, предложенная в 1929 году американскими учеными экономистом П. Дугласом и математиком Ч. Коббом. Она имеет вид
(5.1.14)
и называется производственной функцией Кобба-Дугласа.
Если в функции (5.1.14)
, (5.1.15)
то функцию Кобба Дугласа можно записать в виде
,
То есть
(5.1.16)
Дроби и называются соответственно производительностью труда и капиталовооруженностью труда.
Обозначив производительность труда через x, а его капиталовооруженность через k, исходя из (5.1.16), можно записать
(5.1.17)
Таким образом, из двухфакторной производственной функции (5.1.14) получена формально однофакторная функция (5.1.17). Так как , то из (5.1.17), в частности, следует, что производительность труда в модели Кобба-Дугласа растет медленнее его капиталовооруженности.