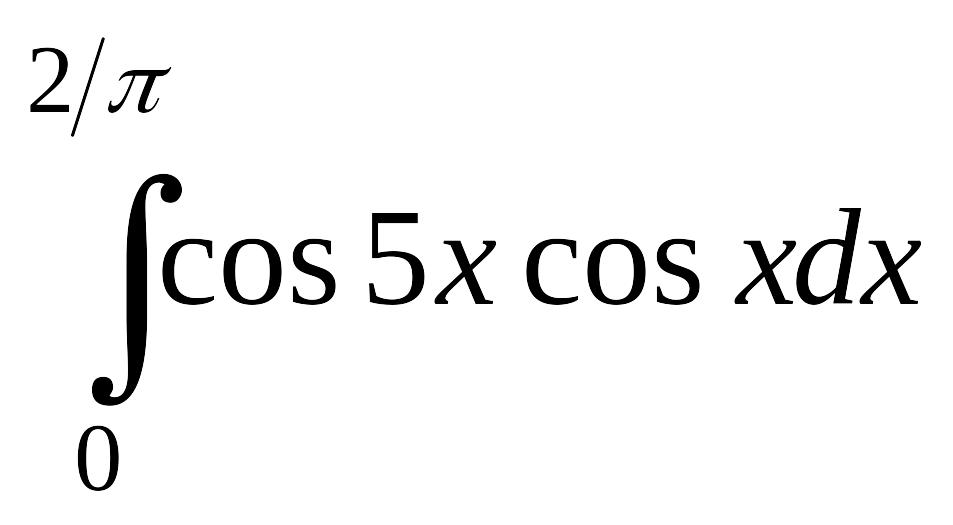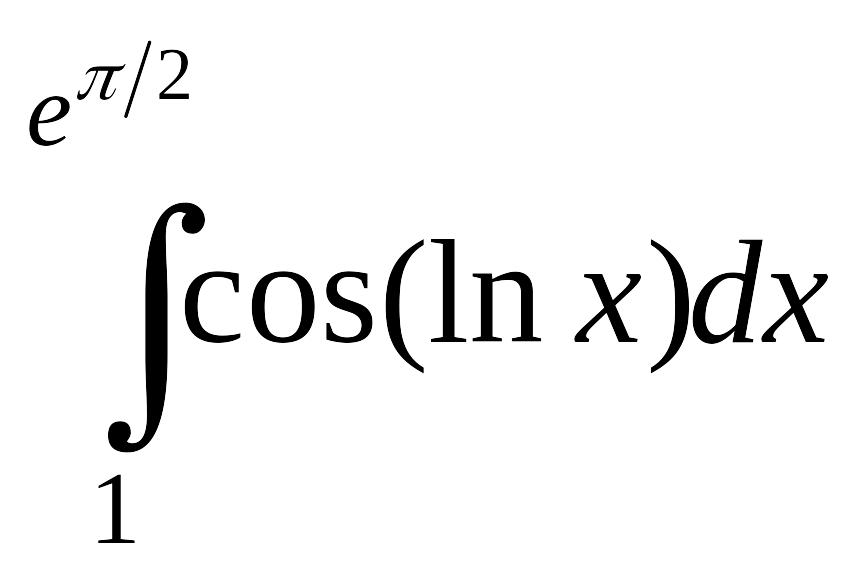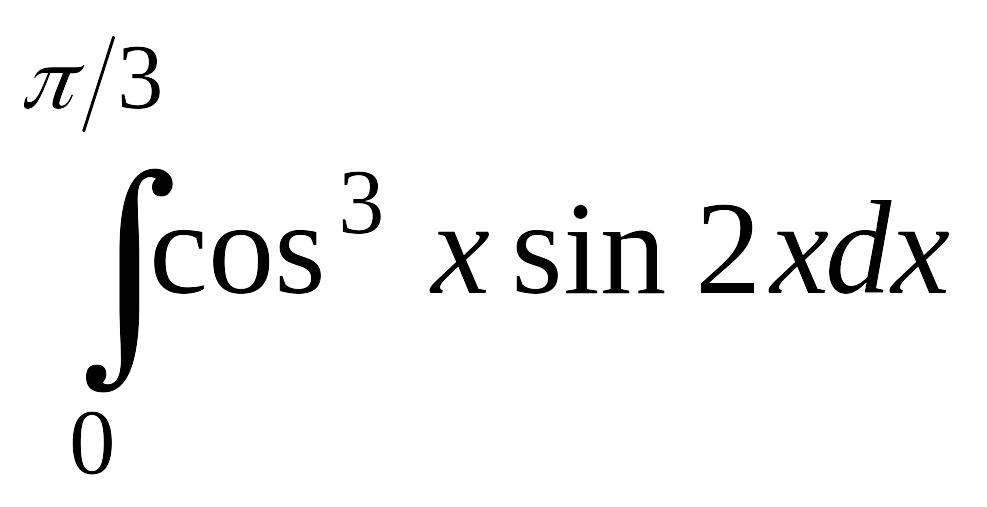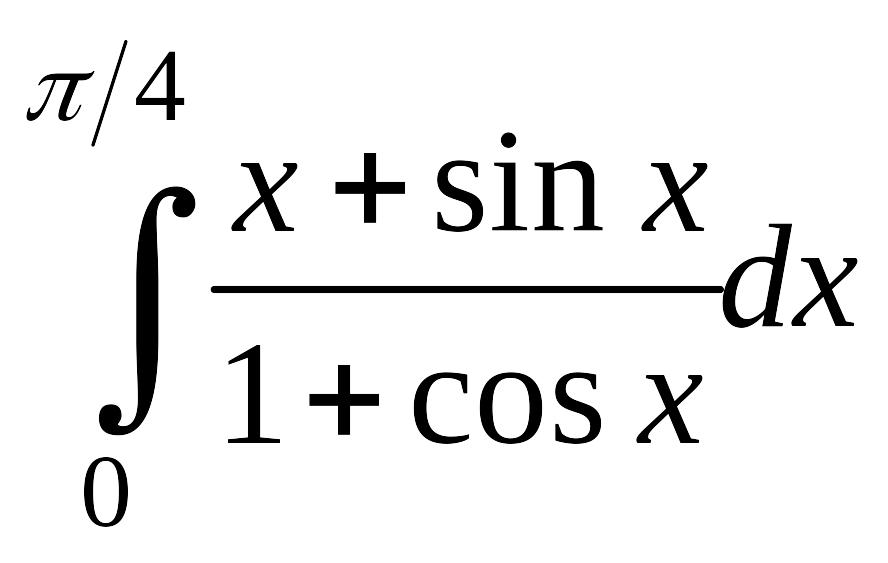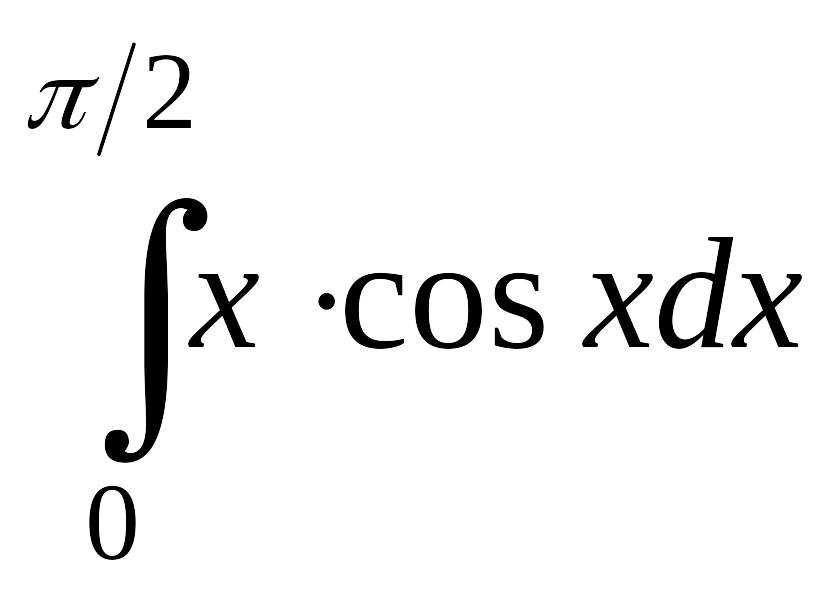Индивидуальные задания Задание 1. Вычисление неопределенных интегралов

Вычислить неопределенные интегралы. Индивидуальное задание в таблице 1

 

Таблица 1. – Индивидуальные задания

№ варианта	Задание
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

 

Задание 2. Вычисление определенных интегралов

2.1. Вычислить определенные интегралы, используя различные встроенные методы численного интегрирования (Romberg, Adaptive Infinite Limit, Singular Endpoint). Индивидуальные задания взять из таблицы 2. Установите различные форматы результатов для различной задаваемой точности.

2.2. Проверить свойства определенного интеграла. Зависимости f1(x) и f2(x) есть подинтегральные выражения из таблицы 2. (Проверку первого свойства осуществлять посредством неопределенного интеграла. Для проверки третьего свойства разбить заданный интервал интегрирования пополам).

Таблица 2. Индивидуальные задания

№ варианта	Задание	№ варианта	Задание
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8		16

 

Задание 3. Вычисления площади, длины дуги и объема с помощью определенных интегралов

3.1. Написать программу-функцию, которая позволяет вычислять площади фигур. Построить графики заданных функций (таблица 3) и вычислить площади фигур, ограниченные линиями.

 

Таблица 3. Индивидуальные задания

№ варианта	Задание	Задание
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

 

3.2. Написать программу-функцию, которая на заданном интервале вычисляет длину заданной кривой. Построить график функции (таблица 4) и вычислить длину дуги заданной кривой.

 

Таблица 4. Индивидуальные задания

№ варианта	Задание	№ варианта	Задание
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8		16

 

3.3* Написать программу-функцию, которая определяет объемы тел вращения. Построить графики кривых и определить объемы тел вращения (таблица 5). Задание общее, выполнить все варианты.

 

Таблица 5. Вычислить объем геометрического тела

1		3
2		4

 

ПРИМЕЧАНИЕ: Дополнительное задание, выполняется для получения оценки выше 8.