
Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении.
Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону).
S=f(t) – уравнение движения точки.
Движение точки определенно, если известны следующие элементы: траектория точки, начало и направление отсчёта дуговой координаты и уравнение движения s=f(t).
Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).
Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).
Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).
В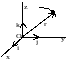 екторный
сп. положение
точки определяется ее радиус-вектором
екторный
сп. положение
точки определяется ее радиус-вектором
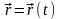 ,
проведенным из какого-либо центра.
Кривая, которая вычерчивается концом
какого-либо вектора, назыв. годографом
этого вектора. Т.е. траектория – годограф
радиус-вектора. Связь между координатным
и векторным способами:
,
проведенным из какого-либо центра.
Кривая, которая вычерчивается концом
какого-либо вектора, назыв. годографом
этого вектора. Т.е. траектория – годограф
радиус-вектора. Связь между координатным
и векторным способами:
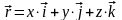 ,
,
(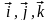 – орты – единичные вектора, сонаправленные
с какой-либо осью)
– орты – единичные вектора, сонаправленные
с какой-либо осью)
модуль
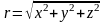 ,
направляющие косинусы:
,
направляющие косинусы:
 и т.д.
и т.д.
Переход
от координатного способа к естественному:
 .
.
Скорость
точки.
Вектор ск-сти:
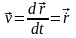 – первая производная от радиус-вектора
по времени (точка обозначает производную
по времени);
– первая производная от радиус-вектора
по времени (точка обозначает производную
по времени);
 .
Проекции скорости:
.
Проекции скорости:
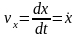 ,
,
 ,
,
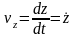 .
Модуль скорости:
.
Модуль скорости:
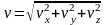 ,
направляющие косинусы:
,
направляющие косинусы:
 и т.д. Если модуль скорости не изменяется
с течением времени, то движение называется
равномерным. При естественном сп.:
и т.д. Если модуль скорости не изменяется
с течением времени, то движение называется
равномерным. При естественном сп.:
 – модуль скорости, вектор скорости:
– модуль скорости, вектор скорости:
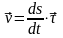 ,
,
 –
орт касательной, т.е. скорость
всегда направлена по касательной к
траектории.
Если v>0,
то движение происходит в сторону
положительного отсчета дуговой
координаты и наоборот. Движение в
полярной системе координат: r=r(t)
– полярный радиус, =(t)
– угол. Проекции скорости на радиальное
направление
–
орт касательной, т.е. скорость
всегда направлена по касательной к
траектории.
Если v>0,
то движение происходит в сторону
положительного отсчета дуговой
координаты и наоборот. Движение в
полярной системе координат: r=r(t)
– полярный радиус, =(t)
– угол. Проекции скорости на радиальное
направление
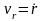 ,
поперечное направление
,
поперечное направление
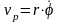 ,
модуль скорости
,
модуль скорости
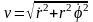 ;
x=rcos,
y=rsin.
;
x=rcos,
y=rsin.
Вектор ускорения точки равен первой производной от скорости или второй производной от радиуса-вектора точки по времени. Вектор ускорения точки имеет направление касательной к годографу скорости. Вектор ускорения точки w расположен в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, =(t) – угол. Проекции скорости на радиальное направление , поперечное направление , модуль скорости ; x=rcos, y=rsin.
При естественном сп.: – модуль скорости, вектор скорости: , – орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, =(t) – угол. Проекции скорости на радиальное направление , поперечное направление , модуль скорости ; x=rcos, y=rsin.
При
естественным сп.
задания движения полное ускорение
раскладывают на нормальное и касательное
(тангенциальное) ускорения:
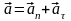 .
Модуль нормального ускорения:
.
Модуль нормального ускорения:
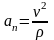 ,
– радиус кривизны траектории, нормальное
ускорение направлено по нормали к
траектории (
к касательной) всегда
к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение
характеризует изменение скорости по
направлению. Модуль касательного
ускорения
,
– радиус кривизны траектории, нормальное
ускорение направлено по нормали к
траектории (
к касательной) всегда
к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение
характеризует изменение скорости по
направлению. Модуль касательного
ускорения
 ,
направлено по касательной к траектории,
либо в сторону скорости, либо в обратную.
Касательное ускорение характеризует
изменение скорости по величине. При
ускоренном движ-ии направление касат.
уск. и скорости совпадают, при замедленном
– противоположно.
,
направлено по касательной к траектории,
либо в сторону скорости, либо в обратную.
Касательное ускорение характеризует
изменение скорости по величине. При
ускоренном движ-ии направление касат.
уск. и скорости совпадают, при замедленном
– противоположно.

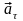 ,
,
 .
Вектор ускорения лежит в соприкасающейся
плоскости
его проекция на бинормаль равна 0
(главная нормаль лежит в соприкасающейся
плоскости, т.е. в плоскости плоской
кривой, бинормаль
–
к главной нормали и касательной).
.
Вектор ускорения лежит в соприкасающейся
плоскости
его проекция на бинормаль равна 0
(главная нормаль лежит в соприкасающейся
плоскости, т.е. в плоскости плоской
кривой, бинормаль
–
к главной нормали и касательной).
Частные случаи движения точки: 1) Прямолинейное: радиус кривизны = (бесконечно большой) аn=0, a=a. 2) Равномерное криволинейное движ-ие: v=const a=0, a=an. Уск. появляется только за счет изменения направления скорости. Закон движ-ия: s=s0+vt, при s0=0 v=s/t.
3) Равномерное прямолинейное движ-ие: а=a=an=0. Единственное движ-ие, где а=0.
4)
Равнопеременное криволинейное движ-ие:
a=const,
v=v0+at,
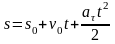 .
При равноуск. движении знаки у a
и v
одинаковы, при равнозамедленном –
разные.
.
При равноуск. движении знаки у a
и v
одинаковы, при равнозамедленном –
разные.
Простейшие движения твердого тела: поступательное и вращение вокруг неподвижной оси. Поступательное движение тела – такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельное самой себе. При поступат. движ. все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Вращательное движение тела – такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела. При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Урав-ние (закон) вращательного движ.: =f(t) – угол поворота тела в радианах. (1 рад= 180о/=57,3о).
Простейшие движения твердого тела: поступательное и вращение вокруг неподвижной оси. Поступательное движение тела – такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельное самой себе. При поступат. движ. все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
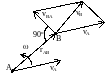
Теорема о скоростях: скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
Теорема об ускорениях: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.
Вращательное движение тела – такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела. При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Урав-ние (закон) вращательного движ.: =f(t) – угол поворота тела в радианах. (1 рад= 180о/=57,3о).
Угловая
ск-сть:
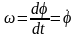 ,
[рад/с] – определяет быстроту изменения
угла поворота.
,
[рад/с] – определяет быстроту изменения
угла поворота.
Вектор
угловой скорости тела, совершающего
вращение вокруг неподвижной оси,
направлен вдоль оси вращения так, что
если смотреть ему навстречу вращение
будет против час. стрелке. "n"–
число оборотов в мин. [об/мин], 1об=2
рад,
 .
Угловое ускорение тела:
.
Угловое ускорение тела:
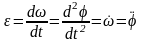 ,
[рад/с2].
Вектор углового ускорения также
направлен вдоль оси вращения. При
ускоренном движении совпадает по
направлению с угловой скоростью и
противоположно при замедленном вращении.
,
[рад/с2].
Вектор углового ускорения также
направлен вдоль оси вращения. При
ускоренном движении совпадает по
направлению с угловой скоростью и
противоположно при замедленном вращении.
Частные случаи вращения тела: 1) Равномерное вращение: =const, =t, =/t,
2)
Равнопеременное вращение: =0+t;
 ,
здесь начальный угол 0=0.
,
здесь начальный угол 0=0.
С корости
и ускорения точек вращающегося тела.
корости
и ускорения точек вращающегося тела.
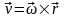 – скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin()=
(CM),
(СМ) – расстояние от точки М до оси
вращения. Направлен вектор скорости
по касательной к окружности, по которой
перемещается точка М, в сторону вращения.
– скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin()=
(CM),
(СМ) – расстояние от точки М до оси
вращения. Направлен вектор скорости
по касательной к окружности, по которой
перемещается точка М, в сторону вращения.
Плоское движение твердого тела.
П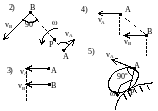


 лоским
(плоскопараллельным) назыв. такое
движение, при котором все его точки
перемещаются параллельно некоторой
неподвижной плоскости. Уравнения
плоского движения:
xA=
f1(t),
yA=
f2(t),
= f3(t),
точка А назыв. полюсом. Плоское движение
тв.тела слагается из поступательного
движения, при котором все точки тела
движутся так же, как полюс (А),и из
вращательного движения вокруг этого
полюса. Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости
точек тела при плоском движении:
лоским
(плоскопараллельным) назыв. такое
движение, при котором все его точки
перемещаются параллельно некоторой
неподвижной плоскости. Уравнения
плоского движения:
xA=
f1(t),
yA=
f2(t),
= f3(t),
точка А назыв. полюсом. Плоское движение
тв.тела слагается из поступательного
движения, при котором все точки тела
движутся так же, как полюс (А),и из
вращательного движения вокруг этого
полюса. Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости
точек тела при плоском движении:
 ;
;
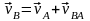 ,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
полюса А. Теорема: при плоском движении
проекции скоростей двух точек тела на
ось, проходящую через эти точки, равны
между собой: vAcos
= vBcos.
Мгновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е.
0,
то мгн.цент.ск. всегда существует. При
поступательном движении м.ц.с. находится
в .
,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
полюса А. Теорема: при плоском движении
проекции скоростей двух точек тела на
ось, проходящую через эти точки, равны
между собой: vAcos
= vBcos.
Мгновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е.
0,
то мгн.цент.ск. всегда существует. При
поступательном движении м.ц.с. находится
в .
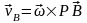 – скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину
отрезка, соединяющего точку с м.ц.с., и
направлена
этому отрезку в сторону вращения фигуры.
– скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину
отрезка, соединяющего точку с м.ц.с., и
направлена
этому отрезку в сторону вращения фигуры.
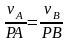 ,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
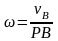 ,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с.
,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с.
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcos = vBcos. Скорости точек тела при плоском движении: ; , vBA= BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А.
‘
Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. 0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в . – скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена этому отрезку в сторону вращения фигуры. , скорости точек тела пропорциональны их расстояниям до м.ц.с. , угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с. Определение положения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. vA и vB); 3) если они при этом равны между собой, то м.ц.с. находится в , а угловая скорость =vA/=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в , и угловая скорость =vA/=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.
Мгновенный
центр ускорений
– точка (Q)
плоской фигуры, ускорение которой в
данный момент времени равно нулю. Для
его построения из точки А откладываем
под углом
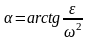 к ускорению аА
отрезок
к ускорению аА
отрезок
 ,
при этом угол откладывается от ускорения
в сторону, направления углового ускорения
.
Модули ускорений точек плоской фигуры
пропорциональны расстояниям от этих
точек до мгн.ц. ускорений, а векторы
ускорений составляют с отрезками,
соединяющими эти точки и м.ц.у. один и
тот же угол
:
,
при этом угол откладывается от ускорения
в сторону, направления углового ускорения
.
Модули ускорений точек плоской фигуры
пропорциональны расстояниям от этих
точек до мгн.ц. ускорений, а векторы
ускорений составляют с отрезками,
соединяющими эти точки и м.ц.у. один и
тот же угол
:
 .
Мгновенный центр скоростей Р и мгновенный
центр ускорений Q
являются различными точками плоской
фигуры.
.
Мгновенный центр скоростей Р и мгновенный
центр ускорений Q
являются различными точками плоской
фигуры.
