Основные понятия кинематики. Скорость точки. Ускорение точки. Определение: Механическое движение – это изменение положения тел в
пространстве с течением времени
Определение: Тело отсчёта – тело, относительно которого рассматривается
положение интересующего нас тела.
Определение: Скорость точки – величина , показывающая как быстро и в
каком направлении происходит движение точки.
Определение: Радиус-вектор – вектор, определяющий положение точки в
пространстве в данный момент времени
Определение: Ускорение точки – кинемат. Мера, харак-ющая быстроту
изменения во времени скорости точки.
Основные задачи кинематики точки и твёрдого тела.
-Кинематика точки:
а) установление различных способов описания движения точки относительно
выбранной системы отсчёта.
б) определение по закону движения точки всех кинемат. Характеристик этого
движения ( траектории, скорости, ускорения и т.д.
- Кинематика твёрдого тела: а) определение положения всех точек тела в сист. отсчёта
б)нахождение их скоростей и ускорений.
Векторный , координатный и естественный способы задания движения
точки.
- Векторный способ задания : Положение точки можно определить с помощью радиус-вектора rM ,
проведённого из некот. Заданной неподвижной точки О в данную точку М.
При движении точки, rМ изменяется по величине и направлению. Каждому
моменту времени соответствует своё знач. rM . ==> rM = rM (t) – кинемат.
уравнение
движения точки в векторной форме.
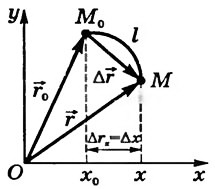
- Координатный способ задания: При нём задаются коорд. точки как ф-ции времени: Xм = F1(t); Yм=F2(t); Zм=F3(t) – уравнени
я траектории в параметр. Виде.
Между векторным и координатным способах задания движения точки сущ. след связь: rM = i* Xм + j* Yм + k*Zм , где i , j , k – орты соответ. Коорд. осей Ox , Oy , Oz.
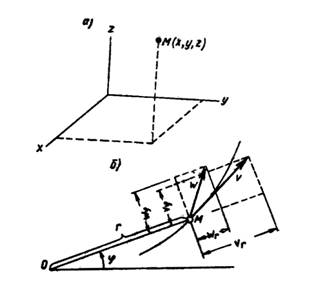
Определение скорости и ускорения точки при векторном способе
задания движения
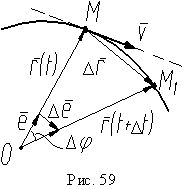
Радиус-вектор r = r (t) определяет положение точки в пространстве в
данный момент времени t, а r = r (t+dt) – в момент времени (t+ Δt).
Изменение d r за dt: d r = r (t+ Δt) - r(t) – перемещение точки за Δt
Отношение dr к dt характериз. среднюю быстроту, с которой произошло
движение точки внутри этого промежутка времени, а также – в каком
направлении оно произошло.
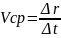– средняя скорость.
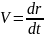– вектор скорости
точки.
(
и направить Vср
по Δr
)
Рассм. 2 близких положения точек М и М1 на траектории. Скорость
т.М обознач. Vм , а т. М1 – Vм1. ΔVм – георметр. Приращение вектора
скорости за Δt.
(
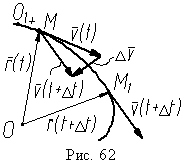направить Аср по ΔV
из т. М)
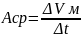, а
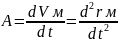, т.к.
5.Определение скорости и ускорения точки при координатном способе
задания движения.
Если движение точки задано: Xм = F1(t); Yм=F2(t); Zм=F3(t) , то скорость
точки определяется по её проекциям на оси координат. Разложим вектор
Vм и радиус-вектор Rм по ортам коорд.осей. Получим
Vм = i*Vx + j*Vy + k*Vz
Rм = i*X + j*Yм + k*Zм , где Xм, Yм и Zм – коорд. движ. точки ; Vx, Vy , Vz
– проекции скорости на оси координат.
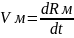
Получим : i*Vx + j*Vy + k*Vz = i*(dXм/dt) + J*(dYм/dt) + k*(dZм/dt) ===>
Vx = (dXm/dt) ; Vy = (dYm/dt); Vz = (dZm/dt)
Для
ускорения
:
Vм
= i*Vx
+ j*Vy
+ k*Vz
Vx = (dXm/dt) ; Vy = (dYm/dt); Vz = (dZm/dt)
A= i*Ax + j*Ay + k*Az = i*(dVx/dt) + j*(dVy/dt) + k*(dVz/dt)
а т.к. v=dX/dt , то Ax=d2Xм/dt2 ; Ay=d2Yм/dt2 ; Az=d2Zм/dt2
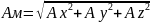
6.---
7.----
8. Поступательное движение тела. Задание движения.
Определение: Поступательным назыв. Движение тела, при котором
любая прямая , проведённая в теле, движется параллельно своему
начальному положению.
Определение: Если при поступательном движении траектории точек тела
прямые линии, то такое движение назыв. Поступат. Прямолинейным.
Определение: Если при поступательном движении траектории точек тела
кривые линии, то такое движение назыв. Поступат. криволинейным.
Отметим, что при поступател. Движении в каждый фикс. Момент времени
скорости (ускорения) точек тела геометр. Равны. Поэтому при поступател.
Движении говорят скорость тела( ускорение тела). ===> при изуч. Поступател.
движения тела достаточно изучить движение только одной (любой) точки.
Для задания поступательного движения твёрдого тела достаточно задать
движение одной из его точек:
Xа = Xa(t)
Ya=Ya(t)
Za=Za(t) ЗНАК СИСТЕМЫ – уравнения поступател. движения тв.тела
9. Поступательное движение тела. Распределение скоростей и ускорений точек
Тела
Определение: Поступательным назыв. Движение тела, при котором
любая прямая , проведённая в теле, движется параллельно своему
начальному положению.
Определение: Если при поступательном движении траектории точек тела
прямые линии, то такое движение назыв. Поступат. Прямолинейным.
Определение: Если при поступательном движении траектории точек тела
кривые линии, то такое движение назыв. Поступат. криволинейным.
Отметим, что при поступател. Движении в каждый фикс. Момент времени
скорости (ускорения) точек тела геометр. Равны. Поэтому при поступател.
Движении говорят скорость тела( ускорение тела). ===> при изуч. Поступател.
движения тела достаточно изучить движение только одной (любой) точки.