2. Первое начало термодинамики. Адиабатный процесс. Уравнение адиабаты. Политропный процесс.
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Первое начал термодинамики утверждает, что количество теплоты, сообщаемое системе, затрачивается на приращение внутренней энергии системы и совершение системой работы над внешними телами:
Q=U2-U1+A
или в дифференциальной форме
d`Q=dU+d`A
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.
Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатические). В общем случае адиабатический процесс необратим.
Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (delta Q = 0) системы со средой имеет вид:
Delta U=-A
Delta U - изменение внутренней энергии тела,
A - работа, совершаемая системой
Delta Q - теплота, полученная системой
Уравнение Пуассона
Для идеальных газов адиабата имеет простейший вид и определяется уравнением:
P*(V^y)=const
где:
p - давление газа,
V - его объём,
Y=Cp/Cv - показатель адиабаты,
Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.
Для идеального газа уравнение политропы может быть записано в виде:
P*(V^n) = const
где величина n=(c-Cp)/(c-Cv) называется показателем политропы.
В зависимости от процесса можно определить значение n:
1. Изотермический процесс: n = 1, так как PV1 = const, значит PV = const, значит T = const.
2. Изобарный процесс: n = 0, так как PV0 = P = const.
3. Адиабатный процесс: n = y, это следует из уравнения Пуассона.
Здесь y (гамма) — показатель адиабаты.
4. Изохорный процесс: n=бесконечности
Билет №11.
1. Инерциальные системы отсчета. Преобразования Галилея. Принцип относительности Галилея.
Среди всевозможных систем отсчета существуют такие ,относительно которых движение тел оказывается особенно простым. В частности, тела, не подверженные воздействию других тел, движутся относительно таких систем без ускорения, т.е. прямолинейно и равномерно. Эти особенные системы отсчета называются инерциальными.
Преобразования Галилея — в классической механике преобразования координат и времени при переходе от одной инерциальной системы отсчета к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают, одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея).
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже больших), преобразования Галилея приближенно верны с очень большой точностью.
Если ИСО S движется относительно ИСО S' с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:
x`= x+ut
y`= y
z`= z
t`= t
или, используя векторные обозначения,
r`(вектор)= r(вектор)+u(вектор)*t
t`= t
(последняя формула остается верной для любого направления осей координат).
Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).
Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:
v`(вектор)= v(вектор)+u(вектор)
a`(вектор)= а(вектор)
Положение о том, что все механические явления в различных инерциальных системах отсчета протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно. Носит название принципа относительности Галилея.
2. Число степеней свободы. Закон равномерного распределения энергии по степени свободы молекул. Внутренняя энергия идеального газа. Классическая молекулярно-кинетическая теория теплоемкости идеального газа. Связь числа степеней свободы молекул с показателем адиабаты.
Число степеней свободы: наименьшее число независимых координат, определяющих положение и конфигурацию молекулы в пространстве.
Модели молекул: а- одноатомной, б- двухатомной, в- трехатомной.
Число степеней свободы для одноатомной молекулы - i=3 (поступательное движение в направлении трех координатных осей), для двухатомной - i=5 (три поступательных и две вращательных, т.к. вращение вокруг оси Х возможно только при очень высоких температурах), для трехатомной - i=6 (три поступательных и три вращательных).
Закон распределения энергии по степеням свободы. На каждую степень свободы приходится в среднем одинаковая кинетическая энергия, равная 1/2kT. 1.
Средняя энергия одной молекулы.
<E >=i(kT/2)
2. Внутренняя энергия одного моля газа
Um=<E>Na=(i/2)k*Na*T
3. Внутренняя энергия произвольной массы газа
U=(m/M)UM=(m/M)(i/2)RT
Na - число Авогадро, k - постоянная Больцмана.
Внутренняя энергия какого-либо тела слагается из кинетической энергии поступательного и вращательного движения молекул, кинетической и потенциальной энергии колебательного движения атомов в молекулах, потенциальной энергии взаимодействия между молекулами и внутримолекулярной энергии (т.е. энергии электронных оболочек атомов и внутриядерной энергии). Кинетическая энергия тела как целого и его потенциальная энергия во внешнем силовом поле во внутреннюю энергию тела не входит.
Внутренняя энергия системы тел слагается из внутренней энергии каждого из тел в отдельности и энергии взаимодействия между телами. Последняя представляет собой энергию взаимодействия в тонком слое на границе между телами, которая столь мала по сравнению с энергией макроскопических тел, что ею можно пренебречь и считать, что внутренняя энергия системы макроскопических тел равна сумме внутренних энергий этих тел.
Внутренняя энергия является функцией состояния системы. Это означает, что независимо от предыстории системы её энергия в данном состоянии имеет присущее этому состоянию значение. Поэтому приращение внутренней энергии при переходе системы из одного состояния в другое всегда равно разности значения внутренней энергии в конечном и начальном состояниях независимо от пути, по которому совершался переход, т.е. независимо от характера процесса, приведшего к переходу системы из одного состояния в другое.
В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна
Ek= (i/2)*kT
Где Ek - кинетическая энергия молекулы
Так как в одном моле содержится Na молекул, то внутренняя энергия одного моля газа будет
U0=Ek*Na=(1/2)Na*kT
где Na - число Авогадро
Учитывая, что k=R/Na , получим
U0= (1/2)*RT
Для любой массы m газа, т.е. для любого числа молей m/M внутренняя энергия
U= (m/M)*(i/2)*RT
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества
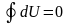интеграл по замкнутому контуру
от dU=0
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
c = Q / (mΔT).
Во многих случаях удобно использовать молярную теплоемкость C:
C = M · c,
где M – молярная масса вещества. Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом.
При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: Cv - молярная теплоемкость в изохорном процессе (V = const) и Cp - молярная теплоемкость в изобарном процессе (p = const). В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Qv = CvΔT = ΔU.
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры. Для процесса при постоянном давлении первый закон термодинамики дает:
Qp = ΔU + p(V2 – V1) = CvΔT + pΔV
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT.
Соотношение, выражающее связь между молярными теплоемкостями Cp и Cv, имеет вид (формула Майера):
Cp = Cv + R.
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости Cv в процессе с постоянным объемом:
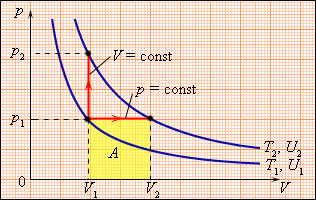
Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV.
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой y (гамма).
y=Cp/Cv
Cv= i*R/2 Cp= (I+2)*R/2
y=(i+2)/i