1. Динамика вращательного движения твердого тела относительно оси. Момент силы и момент импульса относительно оси. Основной закон динамики вращательного движения.

Значительно проще найти момент импульса тела, вращающегося вокруг неподвижной оси z (рис. 1). В этом случае составляющие – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием Mz .

Пусть некоторое тело вращается вокруг оси z (рис. 2).

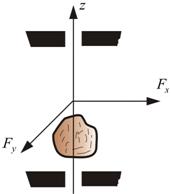
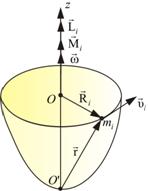
Рис. 1 Рис. 2

Получим уравнение динамики для некоторой точки mi этого тела, находящегося на расстоянии Ri от оси вращения. При этом помним, что L и M направлены всегда вдоль оси вращения z, поэтому

dLi/dt=Mi или d[Ri*mi*v]/dt=Mi

Поскольку vi у всех точек разная, введем вектор угловой скорости wi , причем w=v/R . Тогда .

Так как тело абсолютно твердое, то в процессе вращения mi и Ri останутся неизменными. Тогда

mi*(Ri^2)*(dw/dt)=Mi

Обозначим Ii (и -итое) – момент инерции точки находящейся на расстоянии R от оси вращения:

Ii=mi*(Ri^2) (1)

Момент инерции тела служит мерой инертности во вращательном движении.

В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях от оси вращения. Момент инерции такого тела равен:

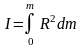I=(интеграл от 0 до m) (R^2)*dm (2)

Как видно, момент инерции I – величина скалярная.

Просуммировав (1) по всем i-м точкам, получим

I*(dw/dt)=M или I*e=M (3)

(e (эпсилон) - угловое ускорение)

Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним: – основное уравнение динамики поступательного движения тела).

Для момента импульса L тела, вращающегося вокруг оси z, имеем:

I*dw=M*dt I*dw=dL L=I*w

При этом помним, что L и M - динамические характеристики вращательного движения, направленные всегда вдоль оси вращения. Причем L определяется направлением вращения, как и w , а направление M зависит от того, ускоряется или замедляется вращение.

(Второй закон Ньютона для вращательного движения):

Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.

M=I*e

где e (эпсилон) - угловое ускорение, I - момент инерции.

2. Термодинамический метод в физике. Параметры, характеризующие макросистемы. Равновесное состояние. Внутренняя энергия. Работа термодинамической системы. Количество теплоты. Теплоемкость системы. Удельная и молярная теплоемкости.

В термодинамическом методе исследования вещества, в отличие от статистического, не вводятся в рассмотрение какие-либо модельные представления об атомно-молекулярном строении тела, а ставится своей задачей установление зависимости между непосредственно наблюдаемыми макроскопическими (измеряемыми в опыте) величинами, такими как давление, температура, объем, концентрация, напряженность электрического или магнитного поля и т. п. Термодинамика как теоретическая дисциплина строится на трех фундаментальных законах (началах), установленных на основании огромного опытного знания, относящегося к поведению макроскопических систем. Выводы термодинамики имеют весьма общий характер, независимый от выбора гипотетической модели структуры вещества, независимо от характера движения молекул, взаимодействия между ними. Результаты, получаемые в статистической теории, существенным образом зависят от выбора этой гипотетической модели. Недостатком термодинамического метода является невозможность с помощью его вскрыть молекулярную сущность изучаемых явлений.

Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объем, энтропия). В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений.

Внутренняя энергия какого-либо тела слагается из кинетической энергии поступательного и вращательного движения молекул, кинетической и потенциальной энергии колебательного движения атомов в молекулах, потенциальной энергии взаимодействия между молекулами и внутримолекулярной энергии (т.е. энергии электронных оболочек атомов и внутриядерной энергии). Кинетическая энергия тела как целого и его потенциальная энергия во внешнем силовом поле во внутреннюю энергию тела не входит.

Внутренняя энергия системы тел слагается из внутренней энергии каждого из тел в отдельности и энергии взаимодействия между телами. Последняя представляет собой энергию взаимодействия в тонком слое на границе между телами, которая столь мала по сравнению с энергией макроскопических тел, что ею можно пренебречь и считать, что внутренняя энергия системы макроскопических тел равна сумме внутренних энергий этих тел.

Внутренняя энергия является функцией состояния системы. Это означает, что независимо от предыстории системы её энергия в данном состоянии имеет присущее этому состоянию значение. Поэтому приращение внутренней энергии при переходе системы из одного состояния в другое всегда равно разности значения внутренней энергии в конечном и начальном состояниях независимо от пути, по которому совершался переход, т.е. независимо от характера процесса, приведшего к переходу системы из одного состояния в другое.

Работа в термодинамическом процессе 1-2 , таким образом, выражается так:

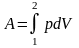A=(интеграл от 1 ( объема в состоянии 1) до 2 ( объема в состоянии 2)) pdV

где p - давление, dV - бесконечно малое приращение объема.

Величина работы зависит от пути, по которому термодинамическая система переходит из состояния 1 в состояние 2, и не является функцией состояния системы. Такие величины называют функциями процесса.

Количество теплоты — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин.

Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.

Теплоемкость, количество теплоты, затрачиваемое для изменения температуры на 1°С. Согласно более строгому определению, теплоемкость - термодинамическая величина, определяемая выражением:

где ΔQ - количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на ΔT. Отношение конечных разностей ΔQ/ΔТ называется средней теплоемкостью, отношение бесконечно малых величин dQ/dT - истинной теплоемкостю. Поскольку dQ не является полным дифференциалом функции состояния, то и теплоемкость зависит от пути перехода между двумя состояниями системы. Различают теплоемкость системы в целом (Дж/К), удельную теплоемкость [Дж/(г·К)], молярную теплоемкость [Дж/(моль·К)].

Удельная теплоёмкость определяется как количество тепловой энергии, необходимой для повышения температуры одного килограмма вещества на один градус Цельсия.

Формула расчёта удельной теплоёмкости:

с=Q/m*delta T

где c - удельная теплоёмкость, Q - количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),m - масса нагреваемого (охлаждающегося) вещества,delat T - разность конечной и начальной температур вещества.

Молярная теплоёмкость — это теплоёмкость одного моля вещества. Часто употребляется обозначение C. Однако буквой C часто обозначается и простая теплоёмкость.

Связь с удельной теплоёмкостью:

С=M*с Cv=(i*R)/2 Сp=((i+2)*R)/2

где с — удельная теплоёмкость, М — молярная масса, Cv - молярная теплоемкость при постоянном объеме,

Сp - молярная теплоемкость при постоянном давлении, i - число степеней свободы (i=3 для одноатомной молекул, i=5 для двухатомной и i=6 для трех- и более атомной молекулы).

Размерность молярной теплоёмкости [Дж/(К•моль)]

Билет № 9.