2. Основное уравнение молекулярно-кинетической теории идеального газа. Молекулярно-кинетическое толкование абсолютной температуры.

P=1/3*n*m0*v^2 (v- среднеквадратичная скорость)

Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.

P=2/3*n*<E>

Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).

Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.

Абсолютный ноль определён как 0 K, что равно −273.15 °C.

Билет №6.

1. Энергия как функция состояния системы. Кинетическая энергия. Теорема об изменении кинетической энергии. Потенциальная энергия. Связь силы с изменением потенциальной энергии.

Величины, характеризующие состояние системы, могут быть неизменными во времени или переменными. В том случае, когда они изменяются, говорят, что изменяется состояние системы. Состояние данной системы обязательно изменяется, если нарушается ее изоляция, то есть когда система приходит во взаимодействие с внешними телами и когда приложенные со стороны этих тел силы совершают работу. Характеристикой состояния системы является ее энергия E, которая не меняет своего значения, если данная система не взаимодействует с внешними телами, а ее изменение в случае взаимодействия равно работе внешних сил.

E2-E1=A

Если работа внешних сил отрицательна, то энергия системы уменьшается, если положительна - энергия возрастает. Работу совершают силы, поэтому можно говорить как о работе внешних сил над системой A, так и о работе A` сил, действующих со стороны системы на внешние тела. Эти работы равны по величине, но отличаются знаками, то есть A=-A` что, по существу, является следствием третьего закона Ньютона. И следовательно, E1-E2=A1

Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Теорема об изменении кинетической энергии материальной точки:

mV2 / 2 - mV02 / 2 = A

то есть: изменение кинетической энергии материальной точки при ее переходе из начального положения в текущее (или конечное) положение равна работе сил, приложенных к точке, совершенной при этом переходе.

Потенциальная энергия U(r) — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.

Зная вид функции U, можно найти силу, действующую на частицу в каждой точке поля. Консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком:

F=-gradu(U)

2. Предмет молекулярной физики. Статистический и термодинамический методы. Основные положения молекулярно кинетической теории. Размеры и сечение столкновения молекул. Число столкновений и длина свободного пробега молекул. Уравнение Ван-дер-Ваальса. Идеальный газ.

Молекулярная физика – раздел курса общей физики, в котором изучаются макроскопические свойства вещества, обусловленные его молекулярным строением, характером движения молекул и силами, действующими между ними.

В основе молекулярной физики лежит установленное на опыте утверждение: в каком бы состоянии не находилось вещество (твердом, жидком, газообразном), составляющие его молекулы находятся в непрерывном хаотическом (непредсказуемом) движении, которое называют тепловым. Хотя движение любой молекулы вещества подчиняется законам механики, описать движение каждой молекулы из большой совокупности (к примеру, в 1м3 воздуха при нормальных условиях находится 2,7•1025 молекул) практически невозможно. В связи с этим в молекулярной физике разработано два взаимно дополняющих друг друга теоретических метода – статистический и термодинамический.

В статистическом методе микроскопические величины, характеризующие движение молекулы (к примеру, ее импульс в данный момент времени), являются непредсказуемыми, случайными. Для построения теории создается гипотетическая модель механизма молекулярного движения и пространственного строения вещества. Затем в этой модели разрабатываются методы нахождения плотности вероятностей тех или иных величин, зная которые вычисляют средние значения этих величин.

В термодинамическом методе исследования вещества, в отличие от статистического, не вводятся в рассмотрение какие-либо модельные представления об атомно-молекулярном строении тела, а ставится своей задачей установление зависимости между непосредственно наблюдаемыми макроскопическими (измеряемыми в опыте) величинами, такими как давление, температура, объем, концентрация, напряженность электрического или магнитного поля и т. п. Термодинамика как теоретическая дисциплина строится на трех фундаментальных законах (началах), установленных на основании огромного опытного знания, относящегося к поведению макроскопических систем. Выводы термодинамики имеют весьма общий характер, независимый от выбора гипотетической модели структуры вещества, независимо от характера движения молекул, взаимодействия между ними. Результаты, получаемые в статистической теории, существенным образом зависят от выбора этой гипотетической модели. Недостатком термодинамического метода является невозможность с помощью его вскрыть молекулярную сущность изучаемых явлений.

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химического вещества. В основе молекулярно-кинетической теории лежат три основных положения:

1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными и состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.

3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Эффективное сечение столкновения молекулы:

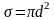s (сигма)=pi*d^2

Где d - эффективный диаметр молекулы (внесистемная единица измерения 1 барн=10^-28 м2).

Среднее число соударений, испытываемых одной молекулой газа в единицу времени

<z>=sqrt(2)*pi*d^2*n*<v>, или <z>=sqrt(2)*s*n*<v>

где d - эффективный диаметр молекулы, n - концентрация молекул, <v> - средняя арифметическая скорость молекул, s (сигма) - эффективное сечение столкновения молекулы.

Средняя длина свободного пробега молекул газа

L=1/(sqrt (2)*pi*d^2*n)

Длина свободного пробега молекулы — это среднее расстояние , которое частица пролетает за время свободного пробега от одного столкновения до следующего.

Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега. Величина является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

(p+(a*v^2/V^2))((V/v)-b)=RT

где

V - объём, v - количество молей газа, p - давление, Т - абсолютная температуры, R - молярная газовая постоянная

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

1. Объём частицы газа равен нулю (то есть, диаметр молекулы пренебрежимо мал по сравнению со средним расстоянием между ними);

2. Импульс передается только при соударениях (то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях);

3. Суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучения)

Билет №7.

1. Импульс частицы. Импульс системы частиц (полный импульс системы). Третий закон Ньютона. Закон сохранения импульса.

Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:

P=mv

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

p=Emv

Третий закон Ньютона.

Силы, с которыми действуют друг на друга взаимодействующие тела, равны по модулю и противоположны по направлению.

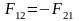F12=-F21

Закон сохранения импульса (Закон сохранения количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

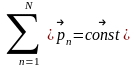p1+p2+p3+…+pn=const

2. Явления переноса. Перенос на трех уровнях: макроскопическом, молекулярном и квантовом. Перенос энергии, импульса и массы на молекулярном уровне. Теплопроводность. Закон Фурье. Коэффициент теплопроводности идеального газа.

Наука, изучающая процессы, возникающие при нарушениях равновесия, носит название физической кинетики.

При нарушении равновесия система стремится вернуться в равновесное состояние. Этот процесс сопровождается возрастанием энтропии и, следовательно, необратим. Таким образом, процессы, изучаемые физической кинетикой, являются необратимыми. Нарушение равновесия сопровождается возникновением потоков либо молекул, либо теплоты, либо электрического заряда и т.п. В связи с этим соответствующие процессы носят название явлений переноса (диффузия, теплопроводность, внутренне трение или вязкость).

Теплопроводность — это перенос тепловой энергии структурными частицами вещества (молекулами, атомами, ионами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Закон теплопроводности Фурье

В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:

q=-L*gradu(T)

где - q вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, L (лямбда) — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору gradu(T) (то есть в сторону скорейшего убывания температуры).

Q=-L*(dT/dx)*S*t (дельта Q)

где Q - количество теплоты, прошедшее посредством теплопроводности через сечение площадью S за время t; L (лямбда) - теплопроводность; dT/dx - градиент температуры.

Коэффициент теплопроводности (L-лямбда) - величина, характеризующая теплопроводящие свойства материала и определяемая плотностью теплового потока при единичной разности температур между поверхностями слоя материала единичной толщины.

L=(Cv*p*<v>*<l>)/3 или L=(i*k*n*<v>*<l>)/6

Где Cv - удельная теплоемкость при постоянном объеме, p - плотность газа, <l> - средняя длина свободного пробега молекул, <v> - средняя арифметическая скорость его молекулы.

Билет № 8