1.Метод конечных разностей

Для сведения дифференциального уравнения к разностному необходимо знать выражения для производных через искомые функции в точках регулярной или нерегулярной сетки.

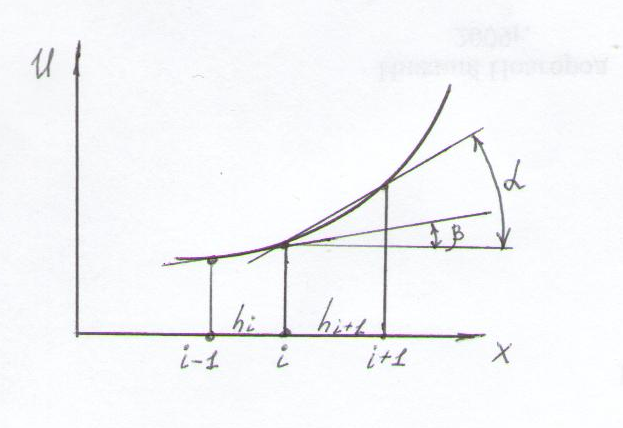
Пусть задана некоторая функция U(x), область определения которой разбита произвольным образом на конечные отрезки. Если h_i=const, то одномерная сеточная область будет регулярной (h_i=h<<1).

Запишем разложение в ряд Тейлора функции в области точки :

(62)

Отсюда найдем:

(63)

или (64)

где - малая величина порядка .

Выражение (64) есть разностное соотношение вперед для первой производной с порядком аппроксимации и равное tg .

Запишем значение через и через ряд Тейлора

(65)

По аналогии с (63) и (64) найдем:

(66)

или (67)

(67)- аналогично, разностное соотношение назад для первой производной с порядком аппроксимации и равное tg .

Сложим и разделим на два выражения (63) и (66). Тогда получим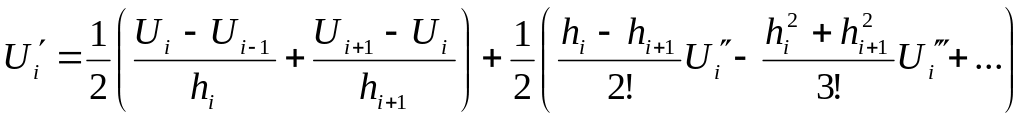

или – центральное конечно-разностное соотношение для первой производной с порядком аппроксимации h_i, равное .

В случае регулярной сетки ( _i= _i+1= ) выражения (64), (67) и (68) запишутся:

= + );

= + ); (69)

= + );

Из (69) следует, что центральное конечно-разностное соотношение имеет более высокий порядок аппроксимации.

Конечно-разностное соотношение для второй производной получим, если из (63) вычтем (66) и выразим отсюда . В результате получим

= [ - ]+0(h) (70)

В случае регулярной сетки (h_i= h_i+1=h)

(71)

Используя конечно-разностные соотношения для можно получить соотношения для 3-й, 4-й и т.д. производных. При h_i=h=const имеем:

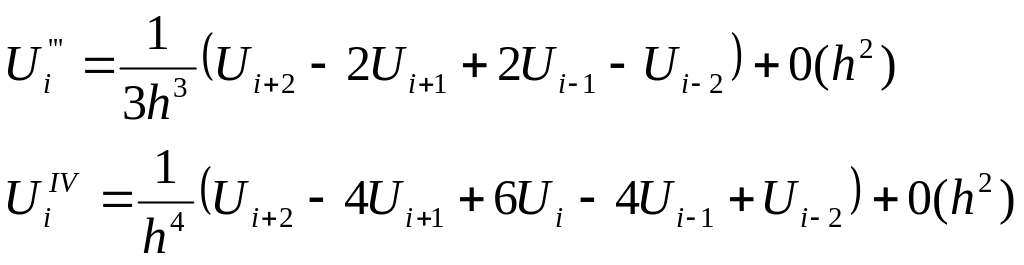
В случае многомерных областей уравнения векторной механики выражаются через дифференциальные уравнения в частных производных.

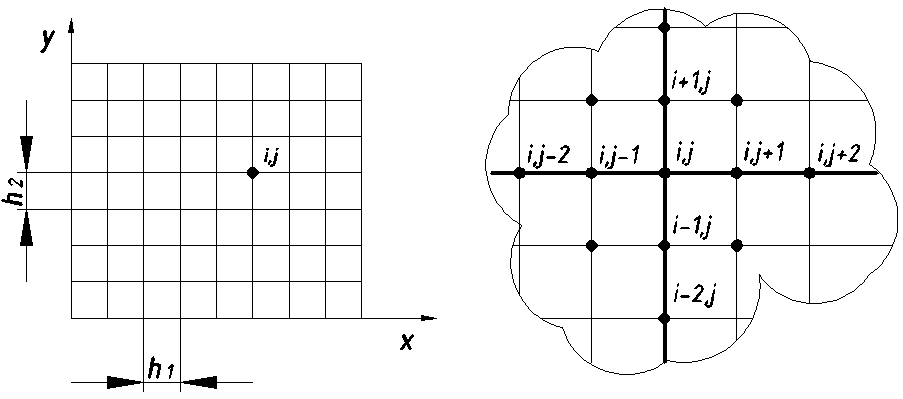
Для прямоугольной сетки с h₁=const и h₂=const конечно-разностные соотношения смешанных производных имеют вид:

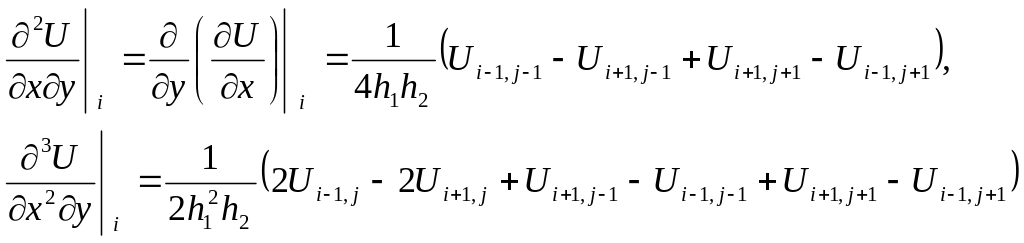
Пример: Определить прогибы и изгибающие моменты в балке переменного поперечного сечения.

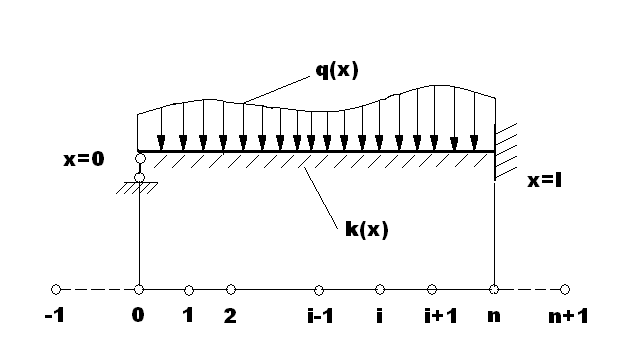
Дифференциальное уравнение изгиба балки имеет вид

(72)

Граничные условия при x=0 при x=l

Введем обозначение

- изгибающий момент.

Тогда вместо (72) получим систему 2-х уравнений:

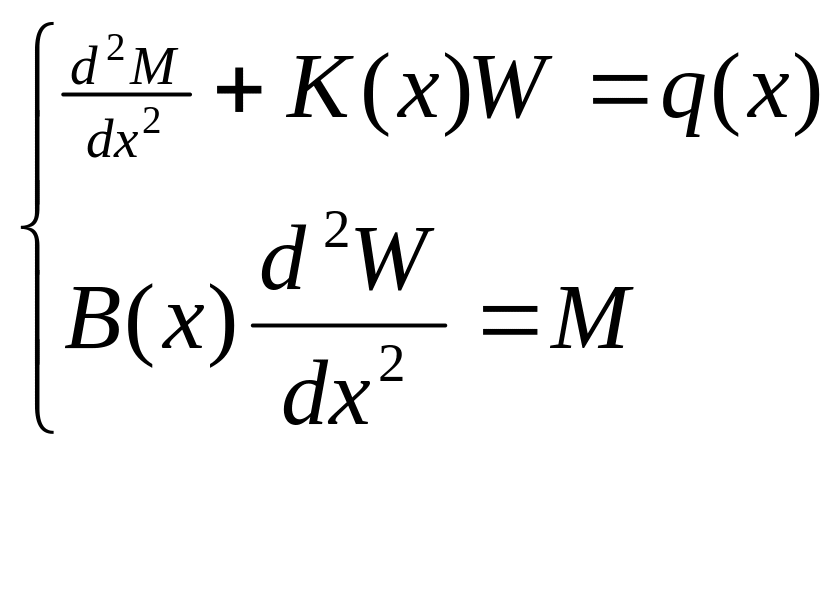(73)

Запишем эту систему для узлов сетки балки, в которых неизвестны М или W, используя конечно-разностные отношения.

Учтем граничные условия:

и , что позволяет исключить из системы (74) законтурное значение прогиба .

В матричной форме система (74) записывается:

(75) Где ;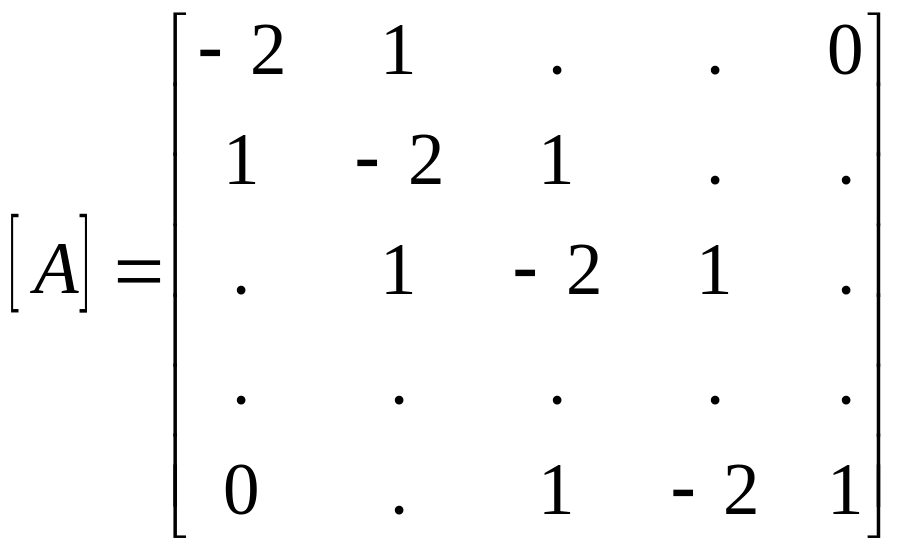

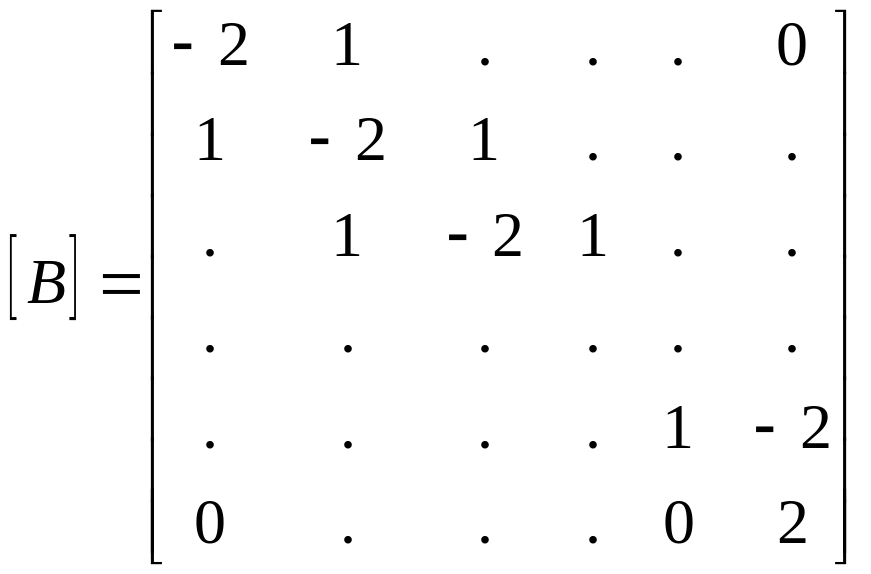
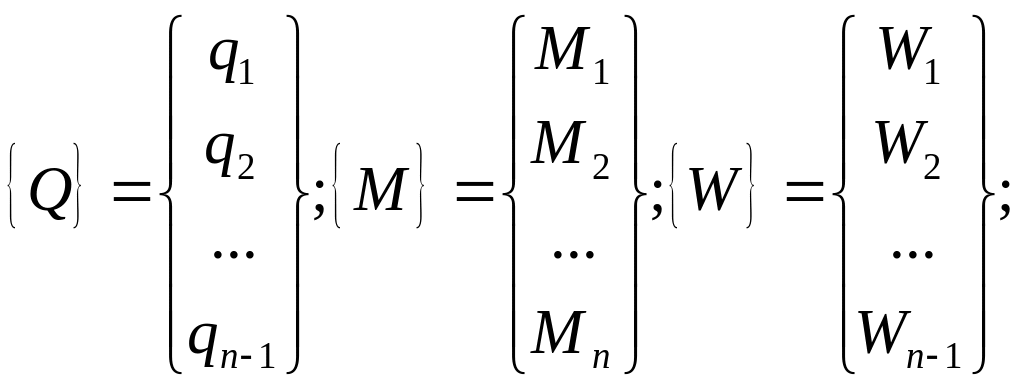
, - диагональные матрицы.

Подставим второе уравнение (75) в первое. Получим:

,где (76)

.

Выражение (76) определяет систему линейных уравнений относительно вектора перемещений .Найдя с помощью второго уравнения (75) можно определить вектор изгибающих моментов .