
- •Машины, механизмы , приборы.
- •Основные характеристики машин.
- •Расчетные модели, схемы.
- •4. Кинематические пары.
- •5. Кинематические цепи.
- •6. Построение и классификация механизмов.
- •9. Внутренние силы в элементах конструкций. Метод сечений.
- •10. Главные центральные оси сечений. Геометрические моменты сечений. Моменты сопротивления изгибу.
- •11. Эпюры внутренних сил и моментов.
- •12. Напряжения и деформации (общий случай).
- •13. Напряжения и деформации при растяжении. Закон Гука.
- •14. Потенциальная энергия деформации.
- •15. Определение напряжений при растяжений стержня на площадках расположенных под углом к оси стержня.
- •16. Механические свойства материалов.
- •17. Сдвиг элементов конструкции.
- •Кручение элементов конструкций. Условие прочности и условие жесткости при кручении.
- •19. Изгиб стержней. Понятия силовой плоскости и плоскости изгиба. Чистый изгиб.
- •20. Расчет опорных реакций. Типы опор.
- •21. Определение внутренних силовых факторов (q,m) при изгибе стержня.
- •22. Нормальные напряжения при изгибе.
- •23. Касательные напряжения при изгибе.
- •24. Объемное напряженное состояние.
- •25. Применение теорий прочности к различным видам нагружений (растяжение, чистый сдвиг, поперечный изгиб).
- •26. Расчет эквивалентных напряжений по трем (основным) теориям прочности.
- •27. Циклы переменных напряжений и сопротивление усталости.
- •28. Факторы влияющие на сопротивление усталости материалов.
- •29. Механические передачи. Основные сведения.
- •37. Сварные соединения, их достоинства и недостатки. Виды сварок.
- •38. Расчет на прочность стыковых сварных соединений.
- •40. Резьбовые соединения. Общая характеристика. Геометрические параметры метрической резьбы.
- •41. Расчет напряжений в теле болта при его растяжке.
- •42. Расчет резьбовых соединений нагруженных сдвигающими силами.
- •44. (47) .Классификация посадок по характеру сопряжения деталей.
- •46. Размеры деталей, допуски на размеры, поля допусков отверстия, вала.
- •Ø50 н7 прописн. (отверстие)
9. Внутренние силы в элементах конструкций. Метод сечений.
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия.
Д ля
суждения о прочности элемента необходимо
сопоставлять максимальные внутренние
усилия с предельными характеристиками
для данного конструкционного материала.
ля
суждения о прочности элемента необходимо
сопоставлять максимальные внутренние
усилия с предельными характеристиками
для данного конструкционного материала.
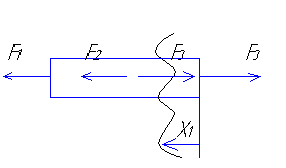
С целью определения внутренних сил используют метод сечений. Чтобы каждая из частей А и Б, были (мысленно) в равновесии под действием нагрузок, необходимо действие отсеченной части заменить системой внутренних нагрузок сечений. Эти внутренние силы являются силами взаимодействия частей А и Б.
В теоретической механике существует такое правило. Любую систему сил, можно свести к точке, например к (центру тяжести сечения) точке и заменить эту систему главным вектором силы и главным моментом.
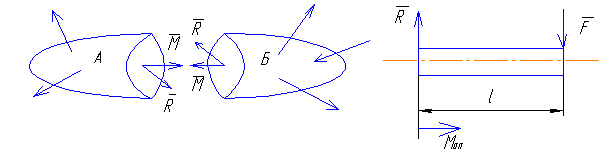

против «+», по часовой «-»
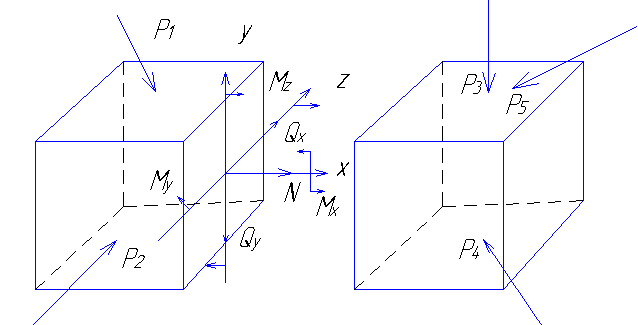
Стержень прямоугольного сечения
![]()
Спроектировав
главный вектор сил
![]() и главный момент
и главный момент
![]() на координатные оси x, y, z,
получаем три силы
Nz ,
Qx ,
Qy
и три момента Mz ,
Mx ,
My ,
называемых внутренними силовыми
факторами в сечении бруса.
на координатные оси x, y, z,
получаем три силы
Nz ,
Qx ,
Qy
и три момента Mz ,
Mx ,
My ,
называемых внутренними силовыми
факторами в сечении бруса.
Составляющая Nz - нормальной, или продольной силой в сечении. Силы Qx и Qy - поперечными усилиями. Момент Mz - крутящим моментом, а моменты Mx и My изгибающими моментами относительно осей x и y.
Компоненты момента


10. Главные центральные оси сечений. Геометрические моменты сечений. Моменты сопротивления изгибу.
Главные центральные оси сечений это такие оси , компоненты которых имеют экстремальные значения. Начало координат в центре тяжести сечения.
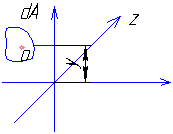





С целью расчета на точность является определение наибольшего опасного сечения, где внутренние силы и моменты имеют максимальное значение по модулю.
Для определения внутренних сил и моментов строится эпюры.
11. Эпюры внутренних сил и моментов.
Э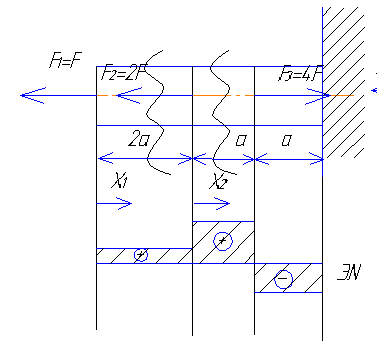 пюра
представляет ряд линий, параллельных
оси. По эпюре устанавливаем максимальное
значение осевой силы.
пюра
представляет ряд линий, параллельных
оси. По эпюре устанавливаем максимальное
значение осевой силы.
![]()
I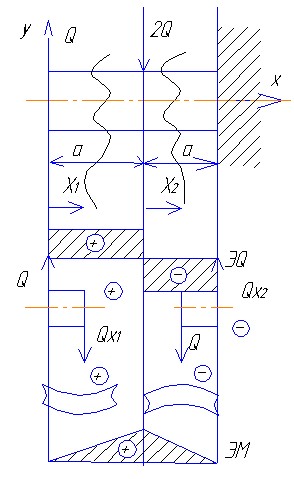 )
)
![]() II)
II)
![]() III)
III)
![]()
Напряжение – это сила действующая на плоскость, это давление.
А – площадь поперечного сечения
![]()
Эпюра напряжения повторяет
![]() ,
,
![]() ,
,
![]() -
напряжение сжатия
-
напряжение сжатия
I)

II)

12. Напряжения и деформации (общий случай).
В
окрестности произвольной точки К,
принадлежащей сечению А
некоторого нагруженного тела, выделим
элементарную площадку А,
в пределах которой действует внутреннее
усилие ![]() (рис. а).
Векторная величина
(рис. а).
Векторная величина
![]()
называется
полным напряжением в точке К.
Проекция вектора полного напряжения
![]() на нормаль к данной площадке обозначается
через
и называется нормальным
напряжением.
на нормаль к данной площадке обозначается
через
и называется нормальным
напряжением.
Векторы и могут быть разложены на нормальную и тангенциальные составляющие.
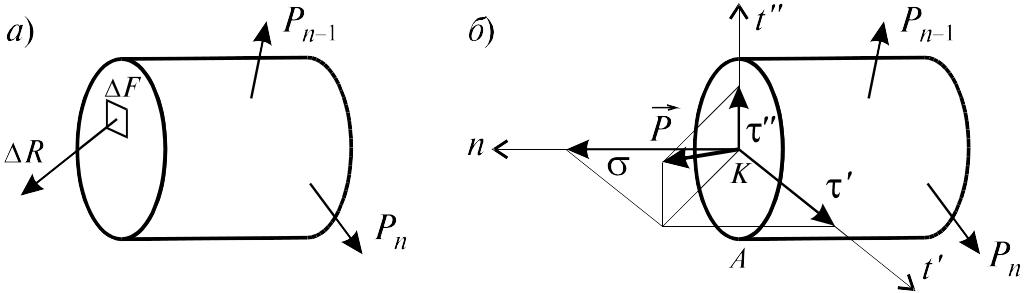
Проекции вектора
![]() на перпендикулярные оси в плоскости
площадки (рис. б) называются
касательными
напряжениями по направлению
соответствующих осей и обозначаются
´
и ´´.
на перпендикулярные оси в плоскости
площадки (рис. б) называются
касательными
напряжениями по направлению
соответствующих осей и обозначаются
´
и ´´.

![]()
Предел
отношения приращения длины отрезка к
его начальной длине
![]()
называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы x , y , z .
Величина
![]() ( DOC DOC) = COD
( DOC DOC) = COD
называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются xy , xz , yz .
Напряжение измеряют по системе СИ 1Н/м²; Паскаль (Па).
