ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

Литература:

1. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.: МАИ, 1992. 262 с.

2. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М.: Энергоатомиздат, 1988.

3. Кук Д., Бейз Г. Компьютерная математика. М. Наука, 1990. 384 с.479 с.

4. Бронштейн Е.М. Множества и функции. Методические указания. Уфа: УГАТУ. 1988.

Определение. Под множеством S будем понимать любое собрание определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами множества S.

Существенной деталью является то, что для любого объекта можно установить, принадлежит он данному множеству S или нет.

Множество задают (специфицируют) двумя способами:

-перечислением: A={1,2,3};

- характеристикой свойств, общих для элементов множества:

А = {X | P(X)} (А - это множество тех и только тех элементов X для которых P от X есть истинное предложение).

Примеры :||

А={1,2,3,4,5,6,7,8};

А- есть множество всех Х, таких, что Х-целое и Х>0 и Х<9;

А={X | X - целое, 0<X<9}.

Если элемент Х принадлежит множеству А, то записывают XA, если не принадлежит, то XA. Например, 7А, 6А.

Определение. Множества А и В считаются равными, если они состоят из одинаковых элементов. Обозначение: А=В.

Например,

{1,2,3} = {2,1,3} = {2,1,1,3}

2  {1,2}, {{1,2}}  {1,2} (Оболочка!)

То есть элемент не считается равным множеству, если даже множество состоит только из этого элемента.

Парадокс Рассела

Описанные выше понятия теории множеств с успехом могут быть использованы в началах анализа, алгебры, математической логики и т. д. Однако при более строгих рассмотрениях такое интуитивное восприятие может оказаться неудовлетворительным.

Приведем в качестве примера парадокс Рассела.

Можно указать такие множества, которые принадлежат самим себе как элементы, например, множество всех множеств.

Можно также указать множества, которые не являются элементами самих себя, например, множество {1,2}, элементами которого являются числа 1 и 2 (других элементов нет).

Рассмотрим теперь множество А всех таких множеств Х, что Х не есть элемент Х.

Тогда, если это полученное множество А не есть элемент А (самого себя), то по определению, А также есть элемент А.

С другой стороны, если А есть элемент А, то А – одно из тех множеств Х, которые не есть элементы самих себя, т.е. А не есть элемент А (не принадлежит A).

В любом случае А есть элемент А и А не есть элемент А.

Парадокс. Тем самым, интуитивная теория множеств – противоречива. Существует боле строгая формализация теории множеств.

Мы лишь укажем, что к парадоксам приводит в ряде случаев попытка объять необъятное: множество всех множеств (существующих в природе и в нашем сознании).

Отношения между множествами

Определение. Говорят, что А содержится в B или что A есть подмножество множества В, если каждый элемент множества А есть элемент множества В.

Отношение включения между множествами (A содержится в B) обозначается знаком , т.е. AB.

Определение. Если AB и AB, то А есть собственное подмножество В и пишут АВ ||.

Например, {1,2}{1,2,3,4}, множество четных чисел есть собственное подмножество множества целых чисел и т.д.

Свойства отношения включения:

- ХХ; (свойство рефлексивности);

- если XY, YZ, то XZ, (свойство транзитивности);

- если XY, YX, то X=Y (свойство антисимметрии).

Примечание. Не надо путать отношения  и . Хотя 1{1}, {1}{{1}}, но 1{{1}}, так как единственным элементом {{1}} является {1}.

Определение. Множество, не содержащее элементов, называется пустым и обозначается . Пустое множество есть подмножество любого множества.

Определение. Множество всех подмножеств A называют множеством - степенью или Булеаном и обозначается B(A).

Пример.

Если А={1,2,3}, то B(А)={,{1},{2},{3},{1,2},{1,3},{2,3},А}.

Утверждение: если A состоит из n элементов, то B(A) состоит из 2ⁿ элементов.

Доказательство:

Перенумеруем все элементы множества А. Введем описание подмножества множества А в виде строки из n бит (ячеек, содержащих цифры 0 или 1). 0 на i-том месте означает, что i-тый элемент не принадлежит данному подмножеству, 1- что принадлежит.

0

1

0

0

…

1

0

1

Например, пустое множество обозначается строкой нулей, само А – строкой единиц.

Тогда число различных комбинаций нулей и единиц равно количеству различных двоичных чисел, которые можно записать в n битах, т.е. 2ⁿ.

Действия над множествами

1) Объединением множеств А и В называется множество всех элементов, которые являются элементами хотя бы одного множества А или В:

AB={x | xA или xB}

Некоторые свойства: AAB, BAB.

Диаграммы Эйлера-Венна. Вводится понятие универсального множества U (множества, содержащего все возможные элементы). Этот универсум обозначается квадратом. Другие множества обозначаются кругами внутри этого квадрата.:

A B

A

A

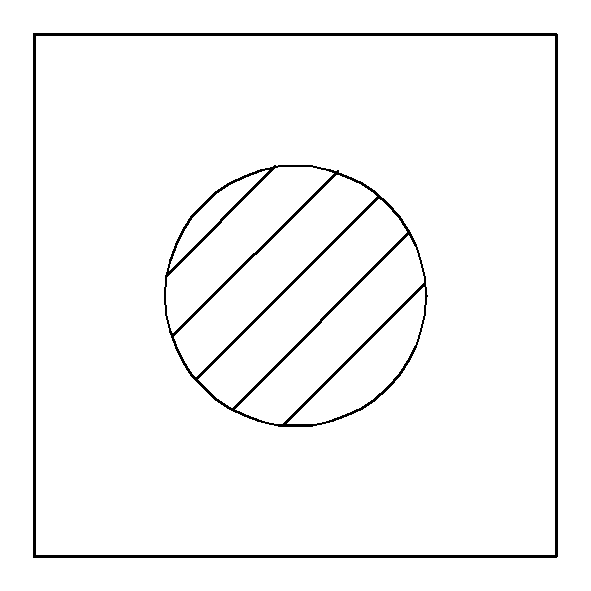
B

2) Пересечением множеств А и В называется множество всех элементов, которые являются элементами обоих множеств А и В:

AB={x | xA и xB}

Некоторые свойства: ABAAB, ABBAB.

A B

A

B

3) Абсолютное дополнение (множество всех элементов, не принадлежащих множеству А): = {x | x A}

A

4) Вычитание множеств или относительное дополнение множества А до множества B: B\A={x | xB, xA}.

Эта операция может быть осуществлена с помощью пересечения и дополнения: B\A=B.

B \ A

B

A

5) Симметрическая разность: A+B=(A\B)(B\A)

A + B

A

B

Свойства действий над множествами. Алгебра теории множеств

1	AВ=BA (коммутативность объединения );		1	AB=BA (коммутативность пересечения);
2	A(BC)=(AB)C (ассоциативность );		2	A(BC)=(AB)C (ассоциативность );
3	A(BC)=(AB)(AC) (дистрибутивность  относительно );		3	A(BC)=(AB)(AC) (дистрибутивность  относительно );
4	A=A;		4	AU=A;
5	A=U;		5	A=;
6	AA=A;		6	AA=A;
7	AU=U;		7	A=;
8	= (закон де Моргана);		8	= (закон де Моргана);
9	A(AB)=A (закон поглощения);		9	A(AB)=A (закон поглощения).

Доказательство свойства 3 (с помощью свойства антисимметрии )

Во-первых, A(BC)(AB)(AC).

Действительно, если xA(BC), то xA или xBC.

Если xA, то xAB и xAC. Тогда x(AB)(AC).

Если xBC, то xB и xC. Тогда xBA и xCA, а значит, x(AB)(AC).

Во-вторых, (AB)(AC)A(BC).

На самом деле, если x(AB)(AC), то xAB и xAC. Тогда xA или (xB и (одновременно) xC), т.е. (xВC). Тем самым, xA(BC).

Из первого и второго следует справедливость утверждения.

Доказательство свойства 8 (=).

Пусть x. Тогда xU и xAB  xA и xB  x и x  x  .

Пусть x. Тогда x и x  xU и xA и xB  xAB, т.е. x  .

В силу справедливости того и другого справедливо и доказываемое утверждение.

Задание

1. Доказать эквивалентность соотношений

1. AB;

2. AB=A;

3. AB=B.

A

B

2. Доказать

а) (AC)(BD)(AB)(CD);

б) (B\C)\(B\A)A\C;

в) A\C(A\B)(B\C);

3. A\(B\C)=(A\B)(AC);

(A\B)C=(AС)\(BC)=(AС)\B.

4. Следует ли из A\B=C равенство A=BC ?

из A=BC равенство A\B=C ?

5. Верны ли равенства

A\(BC)=(A\B)\C ;

A(B\C)=(AB)\C ;

Существуют ли множества?

AB, AC=, (AB)\C=

Решение: AB=B(A)=BA.

Доказать тождества:

а)

б)

в)

г)

д)