Лекции по дискретной математике / LECT11

Лекция №11

Минимальные пути, (маршруты) в нагруженных орграфах (графах)

опр || назовем орграф D=(V,X) нагруженным, если на множестве дуг X определена некоторая функция , которую называют весовой функцией

2

6

7

4

8

Числа – вес дуги, (цена дуги).

Для любого пути П нагруженного орграфа D обозначим через l(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина l называется длиной пути. Если выбрать веса равными 1, то придем к ненагруженному графу.

Опр. Путь в нагр. орграфе из вершины v в верш. w, где vw, называется минимальным, если он имеет наименьшую длину.

Аналогично определяется минимальный маршрут в нагр. графе.

Задачи на min П имеет смысл ставить тогда, когда нет отрицательных замкнутых путей (иначе можно повторять цикл многократно, уменьшая «длину»).

Свойства min путей в нагруженном орграфе

1) Если для  дуги , то  min путь (маршрут) является простой цепью;

2) если min путь (маршрут) то для  i,j : путь (маршрут) тоже является min

Доказывается аналогично св-вам ненагруж. графа.

3) если min путь (маршрут) среди путей (марш.) из v в w, содержащих не более k+1 дуг (ребер), то min путь (маршрут) из v в u среди путей (марш.), содержащих не более k дуг (ребер).

Поиск min пути.

Пусть D=(V,X) – нагр. орграф, V={v₁,… v_n}, n>1. Введем величины , где i=1,…,n, k=1,2,…,n-1.

Для каждого фиксированного i и k величина равна длине min пути среди путей из v₁ в v_i содержащих не более k дуг. Если путей нет, то .

Положим также .

Введем матрицу длин дуг C(D)=[c_ij] порядка n, причем

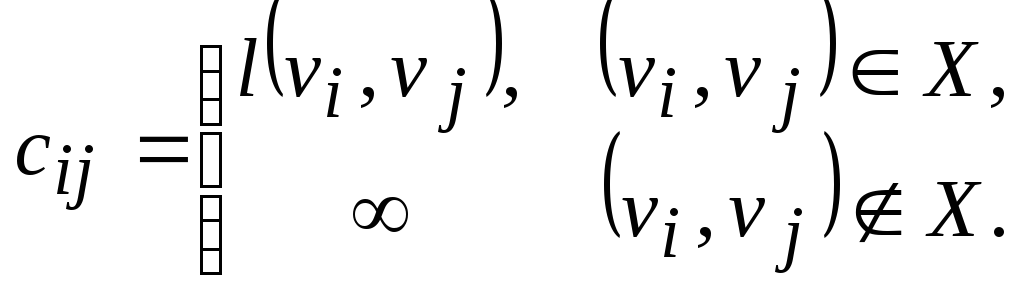
Утверждение. При i=2,…,n, k0 выполняется равенство

(Принцип динамического программирования. Использовать его позволяют свойства 2,3 min путей).

Алгоритм Форда-Беллмана нахождения min пути в нагруженном орграфе D из v₁ в v_i.(i1).

( записываем в виде матрицы, i- строка, k-столбец).

1) Составляем табл. , i=1,…,n, k=0,…,n-1. Если , то пути из v₁ в v_i нет. Конец алгоритма.

2) Если то это число выражает длину любого min пути из v₁ в v_i. Найдем min k₁1, при котором . По определению получим, что k₁- min число дуг в пути среди всех min путей из v₁ в v_i.

3) Затем определяем номера i₂,…, такие, что

,

,

. . . . . . . . . . . . .

,

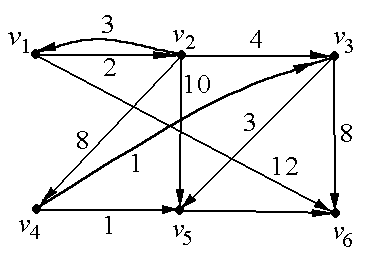
Пример. v₁v₆

	v1	v2	v3	v4	v5	v6
v1			5	5	2	12		0	0	0	0	0	0
v2						2				7	5	5	5
v3		2							5	3	3	3	3
v4		2							5	4	4	4	4
v5			1	2					2	2	2	2	2
v6									12	12	9	7	7

Путь v₁v₆

7=5+2 (2-ая стр.)

5=3+2 (3-я стр.)

3=1+2 (5-я стр.)

2=0+2 (1-я стр.)

Путь v₁v₅v₃v₂v₆

Примеры

Специальные пути в орграфах (маршруты в графах).

Рассмотрим орграфы.

Определение. Свойство  называется латинским, если из того, что путь =₁₂, где ₁, ₂  (множество всех путей в орграфе) обладает свойством , следует, что пути ₁, ₂ также обладают свойством .

Примеры латинских свойств.

1. Не проходить через данную вершину (или через множество вершин).

2. Не проходить через данную дугу (или через множество дуг).

3. Быть простой цепью (или простым контуром).

4. Быть цепью или контуром.

5. Не проходить через каждую вершину более k раз.

Определение. Матричный способ перечисления путей в орграфе, обладающих заданным латинским свойством , называют методом латинской комбинации.

Введем бинарную операцию . Пусть ₁=v₁v₂…v_k_ (мн-во путей, обладающих свойством ), ₂=w₁w₂…w_L_. Положим

Положим ==.

Введем латинскую матрицу размерности nn такую, что - множество путей длины k из v_i в v_j, обладающих свойством , (, если таких путей нет).

Под результатом комбинации будем понимать квадратную матрицу C=[c_ij] порядка n с элементами

(аналогично произведению матриц: строка на столбец).

Утверждение. При любом k1 выполняется

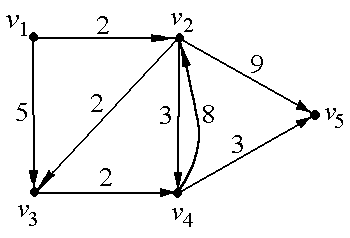
Пример. Найти все простые цепи длины 3 в орграфе D:

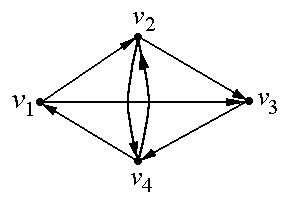
	v1v2	v1v3					v1v2v3	v1v2v4 v1v3v4
		v2v3	v2v4		v2v4v1			v2v3v4
			v3v4		v3v4v1	v3v4v2		
v4v1	v4v2					v4v1v2	v4v1v3 v4v2v3	

	v1v3v4v2		v1v2v3v4
v2v3v4v1		v2v4v1v3	
	v3v4v1v2		
		v4v1v2v3	

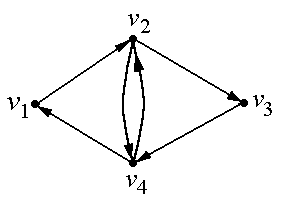
Дополнение. Найти простые контура длины 4 в том же орграфе (свойство ).

Для этого используем матрицу , полученную при решении предыдущей задачи

	v1v2	v1v3	
		v2v3	v2v4
			v3v4
v4v1	v4v2		

	v1v3v4v2		v1v2v3v4
v2v3v4v1		v2v4v1v3		=
	v3v4v1v2		
		v4v1v2v3	

v1v2v3v4v1			
	v2v3v4v1v2		
		v3v4v1v2v3	
			v4v1v2v3v4

Пример 2.