12. Полигармонические и непериодические процессы их спектральные характеристики.

К полигармонич. относ. звук скрипки, саксофона, вибр. двигателя.

К полигармоническим процессам относятся периодические про­цессы, которые математически представляются функцией времени, точно повторяющей свои значения через одинаковые интервалы вре­мени, т. е.

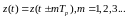
Как и в случае гармонических процессов, интервал времени, в течение которого происходит одно полное колебание, называется периодом Т_р. Число циклов в единицу времени называется фундаментальной частотой f_v. Гармонические процессы представляют собой частный случай полигармонических процессов при f_g= f_p.

В практических случаях полигармонические процессы разлага­ются в ряд Фурье по формуле

,

,

Другое представление полигармонических процессов рядом Фурье дает формула

,

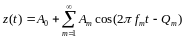
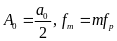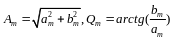
Иначе говоря, формула показывает, что полигармонический процесс есть сумма постоянной составляющей А_о и бесконечного числа гармонических составляющих, называемых гармониками и имеющих амплитуды А_т и фазы Q._m . Все частоты гармонических со­ставляющих кратны фундаментальной частоте f_p.

Однако если процесс образо­ван суммой двух и более гармонических процессов с произвольными частотами, то он, как правило, не будет периодическим. Точнее говоря, сумма двух и более гармонических процессов будет периодическим процессом тогда и только тогда, когда отношение частот любых двух гармоник (входящих в состав всего процесса в целом) есть рациональ­ное число.

Полигармонический процесс может имеет вид, показанный на рис. 5.5, а, и соответствующий формуле (5.5) дискретный спектр, показанный на рис. 5.5, б.

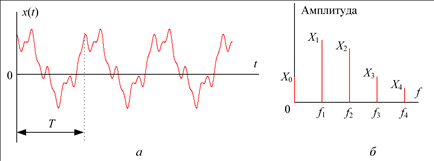
Рис. 5.5. Полигармонический процесс и его спектр

ПОЧТИ ПЕРИОДИЧЕСКИЕ процессы определяются математиче­ски как функции

Причем отношения f_m/f_k не для всех значений индексов явл рациональными числами.

Дискретный спектр почти периодического процесса аналогичен спектру полигармонического процесса.

Переходные см. пункт 1

13. Определение случайного процесса. Непрерывные и дискретные случайные процессы.

Случайный процесс – ординаты принимающие значения из некоторого множества и заранее неизвестно это значение. Реальный случ. процесс набл. в течении ограниченного времени. Случ. процесс, набл. за конечный промежуток времени наз. РЕАЛИЗАЦИЕЙ случ. процесса. Реализация одного и того же процесса отлич. друг от друга, но реализации содержат общие с-ва случ. процесса. Наблюдение за реализацией случ. процесса информации не даёт.

Измерить случ. процесс – определить его статистич. хар-ки, кот. определяются по одной или нескольким реализациям и эти хар-ки отражают с-ва всего процесса. Случ. процесс, набл. за короткий промежуток времени – наз. РЕАЛИЗАЦИЕЙ. Совокупность реализаций случ. процесса наз. АНСАМБЛЕМ.

К хар-кам случ. процесса можно отнести среднее значение квадрата, мат. ожидание, дисперсию, среднеквадрат. отклонение, закон распред-я. Все статистич. хар-тики получ. путём осреднения, при этом осреднение может осущ. осреднением по ансамблю либо осреднению по времени.

Случ. процесс обладает с-вом ЭРГОДИЧНОСТИ, если статистич. хар-ки, найдены осреднением по времени и по ансамблю равны. Будем исходить из гипотезы эргодичности и осреднять будем по времени.

Детерминированные процессы – это процессы, которые можно описать явными математическими формулами. Однако многие физические явления, имеющие место при передаче информации, описываются процессами, которые нельзя считать детерминированными. Например, тепловые шумы в проводной линии связи, или звуковые помехи, маскирующие полезный звуковой сигнал, – это процессы, которые невозможно описать во всех деталях. Совершенно невозможно предсказать точное значение таких процессов в будущие моменты времени. Эти процессы являются случайными (стохастическими) процессами по своей сути, и для их описания требуются вероятностные понятия и статистические характеристики.

Случайный (стохастический) процесс определяется как случайная функция 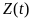от независимой переменной . Определенная функция времени 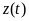, полученная как результат наблюдения процесса , описывающего случайное явление, называется выборочной функцией. Выборочная функция конечной длительности называется реализацией случайного процесса.

Теоретически случайный процесс можно рассматривать как совокупность (ансамбль) 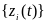всех возможных выборочных функций, которые может дать случайное явление. Следовательно, под реализацией случайного физического явления понимается один из возможных исходов случайного процесса.

Множество возможных реализаций случайного процесса теоретически бесконечно, и неизвестно, какая из этих реализаций будет наблюдаться в текущем эксперименте. Поэтому для любого фиксированного момента времени 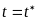(называемого иногда сечением процесса по времени) должно быть задано распределение вероятностей случайной величины .

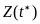Случайные процессы делятся на стационарные и нестационарные. В свою очередь стационарные случайные процессы делятся на эргодические и неэргодические. Дальнейшая классификация нестационарных случайных процессов проводится по особенностям их нестационарностей.

Случайный процесс может быть задан на дискретном множестве значений I: t₁, t₂, ... Это случай сообщения (сигнала), дискретного по времени. Такие случайные процессы называются также случайными последовательностями. Примером случайной последовательностн является процесс X(t_k). заданный на дискретных точках t_1, t₂.... t_k. ... и принимающий в каждой из них значение 1 с вероятностыо pi и 0 с вероятностью p₀=1—pi- независимо от значений в других точках. Чаше встречаются процессы, непрерывные по времени, например, заданные на всей оси —оо<t<оо или на конечном отрезке 0<t<п. — T/2<f< T/2 и т. п. Процессы, заданные на конечном отрезке времени, называются финитными.