48. Корректирующие коды. Ход Хемминга
Вектор ошибок – кодовая комбинация равная длине сообщения, в котором единицами отмечают разряды, в которых произошла ошибка.
Пусть имеется алфавит из N сообщений
E*N – возможное количество ошибок
N – разрешённые кодовые комбинации
N0-N – запрещённые кодовые комбинации
Код Хемминга
k |
k |
|
k |
|
|
|
K |
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
Верхний ряд – отправленное сообщение
Нижний ряд – принятое
Ошибка в разряде a3
a1 |
0001 |
a2 |
0010 |
a3 |
0011 |
a4 |
0100 |
a5 |
0101 |
a6 |
0110 |
a7 |
0111 |
a8 |
1000 |
a9 |
1001 |
Проверка на передаче:
S1-правые разряды с 1 (смотрим в таблице)
S1=a1 a3 a5 a7 a9 = 0 1 0 1 0 =0
S2 – разряд левее S1 и т. д.
S2=a2 a3 a6 a7 = 1 1 1 1 =0
S3=a4 a5 a6 a7 = 0 0 1 1 =0
S4=a8 a9 =0 0 =0
Проверка на приёме:
S1=0 0 0 1 0 =1
S2=1 0 1 1 =1
S3=0 0 1 1 =0
S4=0 0 =0
Считываем суммы в порядке S4, S3, S2, S1 и получаем число 0011, что в десятичной форме равно 3, значит ошибка в разряде a3.
49. Неравномерные коды. Код Хаффмана.
Кодирование по Хаффману выполняется в следующем порядке:
Размещают символы алфавита источника в первом столбце таблицы в порядке убывания их вероятностей.
Суммируют в полученном столбце две последние (наименьшие) вероятности и в результате получают новый столбец таблицы, в котором количество (с учетом суммарной вероятности) значений вероятностей на одну меньше.
Располагают все вероятности в новом столбце порядке убывания.
Повторяют шаги 2) и 3) до тех пор, пока не подучим столбец, состоящий из одной вероятности, равной 1.
По полученным столбцам строится двоичное дерево-граф, начальным узлом которого является последний столбец (вероятность = 1), а выходящие из каждого узла по две ветви отражают процесс объединения вероятностей, выполненный в пунктах 2) и 3).
Затем каждой выходящей из любого узла ветви приписывается 1, если она обладает большей вероятностью и 0, если ее вероятность меньше или равна.
Теперь искомые двоичные кодовые комбинации, соответствующие каждому из символов алфавита источника, можно прочесть из графа, двигаясь по ветвям дерева из начального узла к концевым точкам-вероятностям, отвечающих первому столбцу таблицы.
Таблица кодирования строится как процесс формирования дерева (дерево кодирования Хаффмана).
А также в порядке убывания вероятностей.
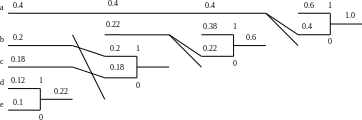
Этим символам ставятся в соответствие листья формируемого дерева. К листу направлена ветвь возле которой записываются вероятности листа. Две самые нижние ветви формируют вершины ветвления, к которой направляется ветвь с суммарной вероятностью далее формируется следующий уровень дерева в которой нижележащие вершины упорядочиваются и так до тех пор пока не будет 1.
После построения дерева ветви исходящие из каждой вершины ветвления. Снабжаются двоичным решением: верхняя ветвь 1, нижняя ветвь 0. Такой алгоритм построения дерева называется методом пузырька т.к. после каждого объединения двух вершин полученная вершина родитель поднимается. Для построения кода осуществляется переход от корня к каждому листу попутно в код заносятся попавшиеся двоичные решения.
На практике можно добиться увеличения эффективности сжатия переопределив алфавит источника следующим образом. Кроме единичных символов в алфавит поместить всевозможные пары символов алфавита. Если считать что символы статистически независимы то вероятности каждого парного элемента будут равны произведению отдельных вероятностей. Затем к полученному алфавиту применить метод Хаффмана. В результате получается код называемый кодом расширения.