36. Амплитудная модуляция.Спектр ам сигнала. Примеры модуляторов.

Амплитудная модуляция-изменение амплитуды сигнала по закону сообщения.

Носитель Ан(t)=А0cos(ω0+ϕ0). Для простоты фазу можно не записывать.

Модулированный носитель: Аx(t)=[ А0+ΔА(t)]cosω0t, здесь ΔА(t) = АmcosΩt

– модулирующая функция, ΔАm – амплитуда модулирующего сигнала, Ω-

его угловая частота.

Аx(t)= А0cosω0t+ ΔАmcosΩt cosω0t= А0(cosω0t+ McosΩt cosω0t).

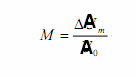- глубина модуляции. Изобразим амплитудно – модулированный

сигнал с глубиной модуляции М=1 (рис. 1.12).

АМ сигнал можно тремя способами:

- принимать весь спектр с полосой 2Ω, что используется в радиовещании;

- принимать обе полосы с подавлением несущей БМ (балансная модуляция с восстановлением несущей в точке приема);

- принимать одну боковую полосу (ОБП) с восстановлением несущей.

Виды модуляторов

По виду управляемых параметров модуляторы делятся на амплитудные, частотные, фазовые, квадратурные, однополосные и т.д. Если несущими являются импульсные сигналы, то их модулируют с помощью амплитудно-импульсных, частотно-импульсных, время-импульсных и широтно-импульсных модуляторов. Качество работы модуляторов определяется линейностью его модуляционных характеристик.

37 Амплитудно-модулируемый сигнал сложной формы, его спектр.

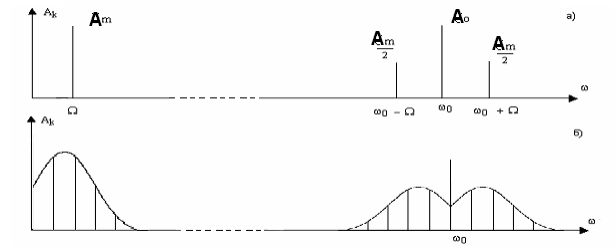
Если управляющий сигнал b(t) обладает более сложным спектром

В этом случае периодический модулирующий сигнал может быть представлен набором гармонических составляющих, частота которых кратна периоду исходного сигнала. Каждая из гармоник модулирующего сигнала сформирует в спектре амплитудно-модулированного колебания две боковые составляющие, симметрично отстоящие от несущей на величину, равную частоте соответствующей гармоники. Для примера, если спектр модулирующего сигнала имеет вид, представленный на рисунке 5.3,а, то спектр амплитудно-модулированного колебания может быть представлен диаграммой, приведенной на рисунке 5.3,б.

Рис. 5.3 Спектры сигналов: а) модулирующего сигнала; б) амплитудно-модулированного колебания

В верхней части этого рисунка изображен спектр управляющего сигнала, а в нижней части — спектр модулированного сигнала

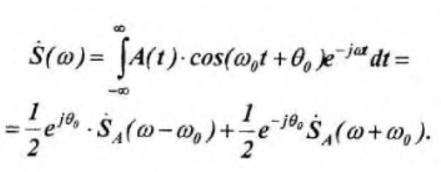
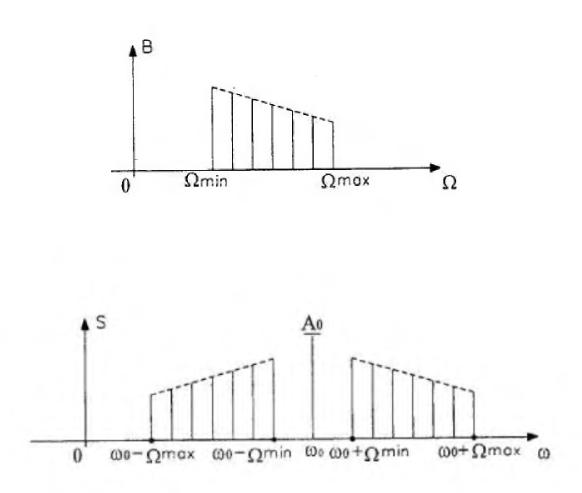
В этом выражении SA(ω) означает спектральную плотность огибающей, т. е. модулирующей функции.

Следует подчеркнуть, что спектр огибающей A(t), как правило, концентрируется в области относительно низких частот. Поэтому функция SA(ω-ω0) существенно отличается от нуля лишь при частотах ω, близких к ω0, т. е. когда разность ω-ω0=Ω относительно мала. Аналогичное слагаемое существует при частотах, близких к — ω0. Таким образом, спектральная плотность модулированного колебания S(ω) образует два всплеска: вблизи ω=ω0 и вблизи ω=-ω0. Спектральные плотности огибающей SA(Ω) и модулированного сигнала представлены на рис. 3.5, причем в реальной системе передачи информации рассматривается только область положительных частот. В современных системах передачи информации широко применяется однополосная модуляция, при которой передача ведется только на одной боковой полосе частот (ОБП).