- •1. Передача информации между двумя оконечными устройствами. Тип соединения оконечных устройств
- •2. Основные определения: информация, сообщение, система связи, сигнал, алфавит.
- •3. Обобщенная структура схемы системы связи
- •4. Источники сообщения в системах связи. Вероятностный характер источников сообщений.
- •5. Форматирование информации. Форматирование текстовых данных. Существующие стандарты.
- •6. Передача сообщений по каналу, искажения, краевые искажения, дробление
- •7. Аналоговые источники сообщений. Преобразование аналоговых сигналов в цифровые. Квантование по уровню. Ошибка квантования.
- •8. Дискретизация аналоговых сигналов по времени. Понятие о теореме Котельникова.
- •9. Преобразование аналоговых сигналов в цифровые. Дискретизация по методу «выборка-хранение». (доработать)
- •10. Сигнал, как реализация процесса. Классификация процессов.
- •11. Классификация процессов. Детерминированные процессы. Гармонические и переходные непериодические процессы.
- •12. Полигармонические и непериодические процессы их спектральные характеристики.
- •13. Определение случайного процесса. Непрерывные и дискретные случайные процессы.
- •14. Измерение случайных процессов.
- •15. Числовые характеристики случайных процессов, их инженерно-физический смысл.
- •16.Законы распределения и основные характеристики случайных процессов
- •17. Автокорреляционная функция случайного процесса. Примеры автокорр. Функций.
- •18. Взаимная корреляционная функция случайных процессов. Примеры применения корреляционных характеристик.
- •19. Усреднение по ансамблю и по времени. Эргодическое свойство случайных процессов.
- •20. Стационарность случайных процессов. Стационарность в широком и узком смыслах.
- •21. Информационные модели сигналов. Формула Хартли.
- •22. Информационные модели сигналов. Формула Шеннона.
- •23. Энтропия источника сообщений. Свойства энтропии источника дискретных сообщений.
- •24. Избыточность при передаче сообщений. Роль избыточности при передаче информации.
- •25. Математические модели сигналов. Временное и частотное представление сигналов.
- •26. Ряд Фурье по произвольной ортогональной системе функций.
- •31. Спектральные характеристики непериодического сигнала. Прямое и обратное преобразования Фурье.
- •32. Оценивание спектральной плотности с помощью дпф
- •33. Дискретное преобразование Фурье (дпф). Гармонический анализ.
- •34. Примеры ортогональных базисов. Функции Уолша.
- •35. Модуляция. Зачем она нужна
- •36. Амплитудная модуляция.Спектр ам сигнала. Примеры модуляторов.
- •37 Амплитудно-модулируемый сигнал сложной формы, его спектр.
- •38 Демодуляция ам сигнала. Работа простейшего амплитудного детектора.
- •43. Спектр колебаний с угловой модуляцией
- •44. Сравнение методов амплитудной и угловой модуляций
- •45. Двоичное представление информации. Механизм восстановления двоичных импульсов.
- •46. Спектральные характеристики случайных процессов.
- •47. Преобразование кодов.
- •48. Корректирующие коды. Ход Хемминга
- •49. Неравномерные коды. Код Хаффмана.
- •50. Неравномерные коды. Код Шеннона-Фано
- •51. Дискретизация аналоговых сигналов по времени. Понятие о теореме котельникова.
- •52. Спектр прямоугольного сиганала
- •53. Свойства энтропии источника дискретных сообщений.
31. Спектральные характеристики непериодического сигнала. Прямое и обратное преобразования Фурье.
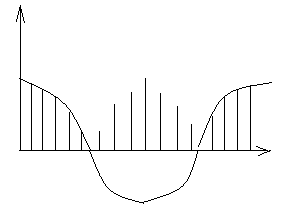
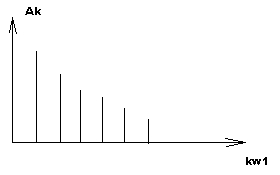
Изобразим периодический сигнал x(t). Оставим неизменной функцию в интервале τ, а период T0 устремим в бесконечность T0→∞. Получим ω0=2π/T0→0, Ак→0. При этом расстояние между составляющими спектра становится бесконечно малым, бесконечно малой становится и амплитуда каждой гармоники. Понятие «амплитудный спектр» заменяется понятием «спектральная плотность амплитуд» S (х) с размерно-
стью амплитуды на единицу частоты В/рад, или S(f) В/Гц.
В отличие от спектра периодических колебаний, спектр которых является дискретным, спектр непериодических колебаний – сплошной.
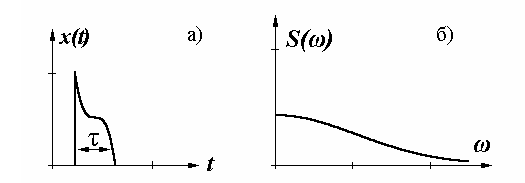
Между непериодическим сигналом x(t) и его спектром S( ω) существует
связь в виде преобразований Фурье:
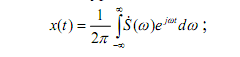
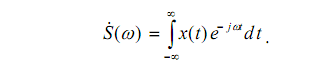
S(ω) называется также комплексной спектральной функцией, эта функция четная, убывающая с ростом частоты.
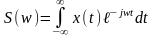 - Прямое преобразование
Фурье (спектральная плотность мощности).
- Прямое преобразование
Фурье (спектральная плотность мощности).
Физический смысл спектральной плотности мощности – комплексная функция частоты одновременно является несущей информацию об амплитуде и фазе элементарных синусоид.
х(t)
=
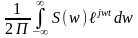 - Обратное преобразование Фурье. По
нему можно восстановить временной
сигнал.
- Обратное преобразование Фурье. По
нему можно восстановить временной
сигнал.
32. Оценивание спектральной плотности с помощью дпф
ДПФ
является комплексной последовательностью
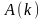 ,
каждый отсчет которой в общем случае
состоит из вещественной и мнимой
компонент:
,
каждый отсчет которой в общем случае
состоит из вещественной и мнимой
компонент:
 , (5.22)
, (5.22)
и может быть представлен в полярной форме как
 ,
,
где
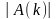
модуль
,
модуль
,
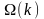
фазовый угол. На практике фазовый угол
представляет интерес для узкого класса
задач, поэтому в основном анализ ведется
по отсчетам модуля
.
Квадрат модуля ДПФ как функция частоты
используется для оценки истинной
спектральной плотности
фазовый угол. На практике фазовый угол
представляет интерес для узкого класса
задач, поэтому в основном анализ ведется
по отсчетам модуля
.
Квадрат модуля ДПФ как функция частоты
используется для оценки истинной
спектральной плотности
 процесса, реализацией которого является
сигнал
процесса, реализацией которого является
сигнал
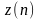 :
:
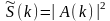 ,
,
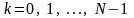 , (5.23)
, (5.23)
где
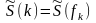 ,
,
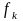
опорные частоты ДПФ, определяемые
формулой (5.12). Заметим, что специалисты-практики
спектром часто называют именно эту
действительную функцию частоты.
опорные частоты ДПФ, определяемые
формулой (5.12). Заметим, что специалисты-практики
спектром часто называют именно эту
действительную функцию частоты.
Можно
показать, что если ДПФ вычисляется по
формуле (5.23), то сумма отсчетов плотности
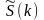 по индексам
по индексам
 приблизительно равна выборочной
дисперсии временного ряда
приблизительно равна выборочной
дисперсии временного ряда
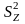 ,
т. е.
,
т. е.
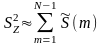 . (5.24)
. (5.24)
Нормированная
спектральная плотность
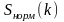 вычисляется по одной из формул:
вычисляется по одной из формул:
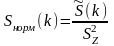 , (5.25
а)
, (5.25
а)
 , (5.25
б)
, (5.25
б)
.
В
большинстве практических задач анализу
подвергаются действительные сигналы
,
ДПФ которых обладает комплексно-сопряженной
симметрией, согласно формуле (5.16).
Следовательно, для действительного
сигнала значения спектральной плотности
симметричны относительно точки
 :
:
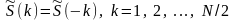 .
.
Поэтому
имеет смысл определять отсчеты
спектральной плотности действительного
ряда только для индексов
 .
.
33. Дискретное преобразование Фурье (дпф). Гармонический анализ.
Предположим,
что непрерывная реализация
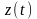 представлена N
эквидистантными
значениями с интервалом дискретизации
представлена N
эквидистантными
значениями с интервалом дискретизации
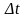 .
Поскольку при рассмотрении финитного
преобразования Фурье мы задавали
интервал определения
как
.
Поскольку при рассмотрении финитного
преобразования Фурье мы задавали
интервал определения
как
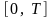 ,
моменты
,
моменты
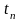 удобно индексировать, начиная с
удобно индексировать, начиная с
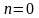 .
Тогда последовательность отсчетов
запишется в виде
.
Тогда последовательность отсчетов
запишется в виде
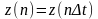 ,
,
 .
.
Дискретная
аппроксимация интеграла (по методу
прямоугольников) в формуле
 при произвольном значении f
есть
при произвольном значении f
есть
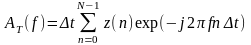 . (5.11)
. (5.11)
Для расчета спектра выбираем дискретные значения частоты
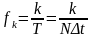 ,
. (5.12)
,
. (5.12)
Формула (5.11) дает на этих частотах следующие составляющие Фурье
 ,
, (5.13)
,
, (5.13)
причем
интервал
внесен в значение
 ,
чтобы избавиться от множителя перед
знаком суммы. Подставив в соотношение
(5.13) выражение для
из (4.12), получим формулу для дискретного
преобразования Фурье
,
чтобы избавиться от множителя перед
знаком суммы. Подставив в соотношение
(5.13) выражение для
из (4.12), получим формулу для дискретного
преобразования Фурье
 ,
. (5.14)
,
. (5.14)
Внимание,
это важно!
Дискретное преобразование Фурье (ДПФ)
применяется для оценивания спектра,
задаваемого соотношением (5.1). Частоты,
определяемые соотношением (5.12), (точки
на оси частот) называются опорными
частотами
ДПФ, а
промежутки
 (интервалы частотной оси) между
последовательными частотами ДПФ –
бинами ДПФ.
Формула (4.14) часто записывается в виде
(интервалы частотной оси) между
последовательными частотами ДПФ –
бинами ДПФ.
Формула (4.14) часто записывается в виде
 ,
,
где ДПФ{} оператор ДПФ.
Свойства ДПФ.
Последовательность периодически повторяется через N значений:
 ,
где
,
где
 .
(5.15)
.
(5.15)
ДПФ действительных временных рядов обладает свойством комплексной симметрии, которое записывается в виде
 ,
,
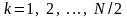 .
.
Учитывая (5.15), последнее соотношение можно представить как
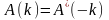 ,
, (5.16)
,
, (5.16)
другими
словами, частоты выше
 можно рассматривать (теоретически) как
отрицательные.
можно рассматривать (теоретически) как
отрицательные.
Значение
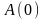 для действительных последовательностей
равно
для действительных последовательностей
равно
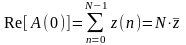 , (5.17)
, (5.17)
 , (5.18)
, (5.18)
где
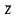
выборочное среднее величин
.
выборочное среднее величин
.
Свойство линейности ДПФ формулируется аналогично (5.5), т. е.
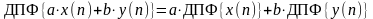 ,
,
где
a
и b
постоянные коэффициенты,
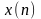 и
и
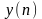
два разных сигнала одина
два разных сигнала одина
ковой длины.
 .
(5.5)
.
(5.5)
Гармонический анализ.Под гармоническим анализом понимают практическое нахождение спектральных характеристик сигнала( Есть сигнал надо найти его спектр). Нахождение коэффициентов Фурье и построение спектров.
x(t)= - Тригонометрическая формула , -комплексная форма,
- Прямое преобразование Фурье (спектральная плотность мощности).
х(t) = - О обратное преобразование Фурье.
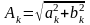 ak
=
ak
=
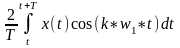 ,
,
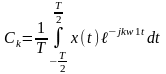

когда мы находим вторую гармонику берем i=2