Цикломатическое число и фундаментальные циклы

Цикломатическим числом графа G=(V,E) называется с k связными компонентами называется число (G)=|E|-|V|+k.

Фундаментальным циклом графа G=(V,E) с остовным деревом T=(V,E') называется простой цикл, получаемый в результате добавления в T одного из ребер G, не принадлежащего E'.

Утверждение 1. Количество фундаментальных циклов графа G=(V,E) при любом фиксированном остовном дереве T=(V,E') равно цикломатическому числу G.

Доказательство: согласно лемме 3 п.2, k=|V|-|E'|, следовательно, <количество ребер G, не принадлежащих E'> = |E|-|E'| = |E|-(|V|-k) = (G). При добавлении любого из этих ребер в T появляется ровно один простой цикл в силу теоремы 3 п.6; все получаемые при этом простые циклы различны, т.к. каждый из них содержит по крайней мере одно уникальное ребро - то самое ребро G, не принадлежащее E', которое было добавлено в дерево.

~

Планарные графы

Сопоставив вершинам графа точки на плоскости или в пространстве, а ребрам - линии, соединяющие точки, соответствующие концам ребра, можно получить диаграмму - визуальное представление данного графа. Очевидно, что для любого графа можно построить бесконечное количество таких диаграмм. Если на некоторой диаграмме среди точек, соответствующих вершинам графа, нет совпадающих, а линии, соответствующие ребрам графа, не имеют общих точек (за исключением концов), то эта диаграмма называется геометрической реализацией графа.

Теорема 1. Для любого графа существует геометрическая реализация в трехмерном евклидовом пространстве.

Доказательство:

1. реализуем |V| точек, соответствующих вершинам графа, на одной прямой;

2. проведем через эту прямую |E| различных полуплоскостей;

3. реализуем каждое ребро в своей полуплоскости.

~

Возникает вопрос: любой ли граф можно реализовать на плоскости? Ответ - отрицательный. Геометрическую реализацию на плоскости допускают лишь некоторые графы; такие графы называются планарными.

Для последующего изложения нам понадобится понятие грани. Неформально определим грань как часть плоскости, на которые плоскость "разрезается" линиями геометрической реализации графа. Всегда существует неограниченная внешняя грань.

- 7 вершин, 8 ребер, 3 грани

Формула Эйлера. Для любой геометрической реализации графа G=(V,E) на плоскости верно: p-q+r=2, где p=|V|, q=|E|, r - число граней (без доказательства).

Теорема 2. Если в связном планарном графе нет циклов длины меньше k и k3, то qk(p-2)/(k-2), где p=|V|, q=|E|.

Доказательство (не совсем формальное): пусть граф реализован на плоскости и при этом получилось r граней. Пусть q_i - число сторон в i-й грани (см. рисунок). Каждое ребро является стороной двух граней, поэтому 2q=Sum(q_i, i=1..r). По условия в графе нет циклов длины меньше k, но тогда q_ik (т.к. стороны грани образуют цикл) и 2q=Sum(q_i, i=1..r)kr. По формуле Эйлера r=2-p+q, следовательно, 2qk(2-p+q), из чего следует доказываемое неравенство.

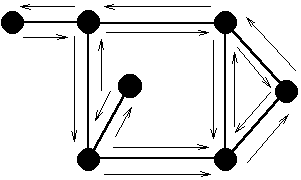- 8 ребер, 3 грани, 3+6+7=16 сторон ~

Следствие 1 теоремы 2: для любого связного планарного графа без петель и кратных ребер выполняется неравенство: q3(p-2), где p=|V|, q=|E|.

Доказательство: т.к. по условию в графе нет петель и кратных ребер, в нем нет и циклов длины меньше 3, поэтому, подставляя k=3 в неравенство теоремы 2, получаем: qk(p-2)/(k-2)=3(p-2).

~

Теорема 3. Граф K₅ не планарен.

Доказательство: K₅ связен, в нем нет петель и кратных ребер, но следствие 1 теоремы 2 не выполняется - q=10>3(p-2)=9. Значит, K₅ не планарен.

~

Теорема 4. Граф K₃₃ не планарен.

Замечание: использование следствия 1 теоремы 2 здесь не поможет, т.к. q=9<3(p-2)=12.

Доказательство: в K₃₃ нет циклов длины меньше 4, поэтому применим неравенство теоремы 2 непосредственно (при k=4): q=9>4(p-2)/2=8. Следовательно, K₃₃ не планарен.

~

Теорема Понтрягина-Куратовского (критерий планарности графов). Граф G планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K₅ или K₃₃.

Доказательство: необходимость следует из утверждений 1-4 (см. ниже), а также из того факта, что графы K₅ и K₃₃ не планарны (в соответствии с теоремами 3 и 4).

Утверждение 1: если графы U₁ и U₂ изоморфны, то U₁ планарен тогда и только тогда, когда U₂ планарен.

Доказательство: любая геометрическая реализация U₁ является геометрической реализацией U₂, и наоборот.

Утверждение 2: любое подразделение U' графа U планарно тогда и только тогда, когда U планарен.

Доказательство: (=>) граф U' планарен, следовательно, существует его геометрическая реализация на плоскости R'. Построим по R' плоскую геометрическую реализацию R графа U. Для этого объединим все линии R', соответствующие ребрам U', полученным в результате выполнения операций подразделения ребер. В силу существования R граф U является планарным. <=) граф U планарен, следовательно, существует его геометрическая реализация на плоскости R. Построим по R плоскую геометрическую реализацию R' графа U'. Для этого повторим в любой последовательности операции подразделения ребер, которые привели к построению U'. После выполнения каждой из этих операций будем разбивать линию, соответствующую подразделяемому ребру, на две линии (разбиение можно производить в любой точке, не совпадающей с концами линии). В силу существования R' граф U' является планарным. Утверждение 3: если графы U₁ и U₂ гомеоморфны, то U₁ планарен тогда и только тогда, когда U₂ планарен.

Доказательство: (=>) по условию U₁ и U₂ гомеоморфны  {по определению}  существуют их изоморфные подразделения U₁' и U₂'. По условию граф U₁ планарен  {по утв.2}  граф U₁' планарен  {по утв.1}  изоморфный ему граф U₂' планарен  {по утв.2}  граф U₂ планарен. (<=) аналогично.

Утверждение 4: если подграф U' графа U не планарен, то U также не планарен.

Доказательство: допустим, что граф U планарен. Следовательно, существует его плоская геометрическая реализация R. Но тогда можно построить плоскую геометрическую реализацию R' графа U': для этого достаточно удалить из R точки и линии, соответствующие тем вершинам и ребрам U, которых нет в U'. Из существования R' следует, что U' планарен - получили противоречие.

Достаточность теоремы доказывается гораздо сложнее (см., например, [3]).

~

Существуют и другие критерии планарности графов [3].