Угловая скорость измеряется в радианах в секунду - [ c-1 ]; угловое ускорение - в радианах в секунду за секунду - [ c-2 ].

 

Нестандартной, но часто применяемой в технике,  единицей измерения  угловой  скорости вращающегося тела является число его оборотов в минуту - n  об./ мин.

 Перевести  число оборотов в минуту  в радианы в секунду совсем  несложно : 

Вращение тела,  как и движение точки, может быть равномерным, ускоренным или замедленным.   В частных случаях (при = const) - равноускоренным или равнозамедленным.  

При известном положительном направлении отсчета угла поворота  направление вращения тела определяется знаком производной (в данном случае d/dt),  а характер движения - сопоставлением знаков производных   d/dt    и   d/dt .      

         Аналогия формул объясняется  весьма просто.  Движение точки по кривой и вращение тела относительно неподвижной оси описывается одной обобщенной  координатой  (точка на заданной кривой и тело,  вращающееся относительно неподвижной оси,  имеют одну степень свободы ).    В первом случае   q(t)  =  S(t),    а  во  втором    q(t)  = (t).

          Выведем далее уже, должно быть, знакомые Вам  формулы для определения  скоростей  и  ускорений  точек  вращающегося  тела. 

          Возьмем точку М, находящуюся на рисунке выше  в подвижной полуплоскости на расстоянии R от оси вращения, и определим ее движение по окружности уравнением  S = S(t).  Начало отсчета дуговой координаты совместим  с   точкой О   неподвижной  плоскости.

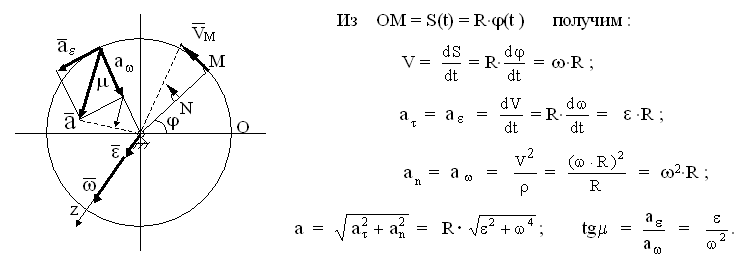
   Необходимо отметить,  что  скорость  точки  вращающегося тела  часто называют  вращательной или окружной скоростью,  а  слагаемые ускорения называют вращательным и осестремительным.  Введем для этих слагаемых ускорения точки при вращательном  движении  специальные обозначения  -      a_  и  a_ ,   с  индексами,  которые будут подсказывать необходимые для их определения формулы. 

И запомним необходимые формулы в виде:

      И,  наконец,  посмотрев на рисунок выше и  формулы,  отметим следующее:

 1.  Скорости точек вращающегося тела,  слагаемые ускорения и полные ускорения  прямо пропорциональны  расстояниям точек до оси  вращения.

2.  Векторы скоростей точек перпендикулярны их радиусам.

3.  Векторы ускорений всех точек тела образуют с их радиусами одинаковые углы  - .

4.  Величина угла    зависит только от характеристик вращательного движения  тела в каждый рассматриваемый момент времени.

          Все это значит, что по вектору скорости или ускорения одной точки вращающегося тела  либо графическим путем, либо расчетом можно определить скорость или ускорение другой точки тела, расположенной на том же радиусе  или любом  другом.

Для их получения мы введем два новых вектора - вектор угловой скорости вращающегося тела - ,  вектор углового ускорения -     и  вращающуюся  систему  координатных  осей.

          У любого вращающегося тела можно выделить три характеристики: величину угловой скорости вращения,  положение оси вращения в пространстве и  направление вращения.  С аналогичными характеристиками мы уже встречались в разделе “Статика”,  рассматривая действие на тело пары сил или определяя вектор-момент силы относительно точки.  Все перечисленные характеристики вращающегося тела  можно задать одним вектором  - , что в механике  и  было сделано.

 

         Вышеприведенные формулы называют формулами Пуассона. Их  легко получить, если:  вспомнить физический смысл производной по времени от переменного вектора;   построить годограф одного из вращающихся ортов;  определить скорость движения конца вектора  по его годографу  как вектора,  перпендикулярного и орту, и вектору угловой скорости,  с  помощью векторного произведения.

 

         В  этой формуле знакомые нам  слагаемые  ускорения точки при вращательном движении тела  -  вращательное  и  осестремительное - определены не только по величине,  но и по направлению. Вектор вращательного ускорения, как и вектор скорости, направлен перпендикулярно радиусу вращения точки  и  в соответствии с характером вращения;  вектор осестремительного ускорения направлен к оси вращения.

        Поэтому постараемся запомнить нижеприведенные формулы  и их вывод.

          В  заключение темы “Вращательное движение тел”  (плакат 9)  необходимо остановиться на  механизмах  для  передачи  вращательного движения  от одного тела к другому.  В технике таких механизмов огромное разнообразие и количество.  В  общем случае их  называют передаточными механизмами.

         С помощью передаточных механизмов вращение тела с одной угловой скоростью преобразовывают во вращение другого тела с иной угловой скоростью.   А возможно, и  в ином направлении. Используются фрикционные (за счет трения),  ременные, цепные, зубчатые,  червячные и иные передачи.  Для значительного изменения  угловой  скорости  используются  редукторы.

       Решая задачи кинематики, необходимо научиться быстро и правильно находить угловые скорости связанных между собой тел, скорости и ускорения отдельных точек тел.

       Некоторые виды передач схематично представлены на плакате 10к.  Здесь же мы рассмотрим простейший случай передачи вращения от одного  вращающегося  тела  другому.

П усть колесо 1,  имеющее  радиус r₁  и число  зубьев  z₁ ,  приводит во  вращение  колесо 2  радиуса  r₂  (число зубьев - z₂ ). Колесо 1 имеет  угловую скорость  .   Требуется найти угловую скорость второго колеса.

 

     Все расчеты в таких передачах проводятся по скоростям точек касания вращающихся тел,  а при отсутствии прямого контакта - по скорости движения соединяющей тела связи ( ремня или цепи ).  Считается, что проскальзывание ремня по поверхности шкива  или в точке контакта тел при передаче вращения за счет сил трения отсутствует.

Скорости  точек касания выражаются через угловые скорости тел и  их радиусы.                        

 .

Из вышеприведенного равенства и получают известную пропорцию.

 

         Угловые  скорости  находящихся  в  зацеплении  тел  вращения

обратно  пропорциональны  их  радиусам

 

            (  или  числам  зубьев  взаимодействующих  шестерен     z₁  и   z₂  ) .

         Отношение угловой скорости ведущего вала к угловой скорости ведомого ( выходного )  вала  принято называть передаточным отношением.

       1.2.3.    СФЕРИЧЕСКОЕ  ДВИЖЕНИЕ  ТВЕРДОГО  ТЕЛА

         Сферическим называют движение тела относительно некоторой  неподвижной точки.  Называют  его  так потому,  что все точки тела   движутся по поверхностям сфер,  радиусы которых определяются расстояниями точек до неподвижной точки.  Чисто сферическое движение в  механике встречается не так уж часто. Такое движение совершают конические барабаны специальных мельниц, конические шестерни в дифференциальных передачах,  знакомые всем с  детства  волчки.  Более часто сферическое движение является составной частью сложного движения тела. Общий случай движения твердого тела рассматривается как совокупность поступательного и сферического движений.

          Неподвижная точка тела при его  сферическом  движении  может быть вполне осязаемой,  как у волчка, а может быть чисто геометрической, как у усеченного конуса при его качении  по  плоскости. 

         Впервые описал движение тела относительно неподвижной  точки Леонард Эйлер.  Он показал, что для определения положения  связанной с телом системы координатных осей относительно неподвижной системы координат  необходимо задать всего три  зависимости:  как изменяются  с течением времени три угла,  которые в механике и названы углами Эйлера.

Это углы прецессии,  нутации и собственного  вращения тела.

( Термины для названий углов взяты из небесной механики )

          Введем для описания сферического движения тела две системы  координатных осей - неподвижную ОXYZ  и связанную с телом подвижную  систему Oxyz  с общим началом в точке О.  Будем считать, что положение подвижной системы координат   Oxyz  задано не изображенными на рисунке  векторами-ортами   ,  и .

П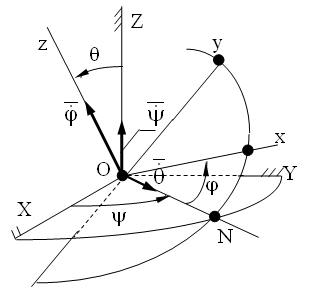 одвижная плоскость  xOy  пересекает неподвижную  XOY  по  некоторой линии ON,  положение  которой  на  плоскости XOY  при движении тела постоянно меняется.

Эту проходящую через неподвижную точку линию ON принято называть линией узлов.

Угол  между линией узлов и осью  OX называют  углом  прецессии.  Этот угол откладывается первым для  определения положения подвижной системы координатных осей  относительно неподвижной.

Линия узлов определяет положение вертикальной плоскости,  в  которой  находится ось собственного вращения тела  (ZOz).

            Положение оси собственного вращения по отношении к неподвижной вертикальной оси OZ  (оси прецессии) определяет  угол    -  угол нутации.

Оси Ox и Oy подвижной системы координат расположены в  плоскости,  перпендикулярной оси собственного вращения тела.   Положение оси  Ox  по отношению к линии узлов в этой плоскости определяется углом .