1.2. Виды движения твердых тел

          Различают пять  видов  движения твердых тел:  поступательное, вращательное,  плоское (называемое также плоскопараллельным), сферическое движение (иначе оно называется движением тела относительно неподвижной точки) и общий случай движения. Два вида движения - поступательное и вращательное - являются простейшими. Остальные виды движения тел рассматриваются как более сложные, т.е. состоящие из отмеченных выше простых движений.

1.2.1. Поступательное движение тела Поступательным называют такое движение тела, при котором любая прямая, связанная с телом, перемещается параллельно своему начальному положению.

 В механике  движущиеся поступательно тела часто рассматривают как материальные точки. Связано это с особенностями движения точек тел при р ассматриваемом виде движения,  которые определяет следующая  теорема.

ПРИ  ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ ТЕЛА

1. Траектории всех точек одинаковы.

2. Скорости всех точек равны.

3. Ускорения всех точек равны.

 

Для доказательства теоремы свяжем между собой  две произвольные  точки

 А и  В  движущегося  поступательно твердого тела вектором . 

           Положение точек А и В по отношению к неподвижной системе 

            координатных осей  определим радиус-векторами   и  .

 Из векторного треугольника следует, что в любой момент  движения тела                                                            = + .

Вектор  постоянен и по величине,  и  по  направлению.  Поэтому траекторию точки В  можно получить простым сдвигом траектории точки А в направлении  вектора .   Траектории точек А и В  при наложении,  естественно, должны совпадать.  Дифференцируя далее по времени записанное векторное равенство,  легко  получить,  что:

   Все пункты теоремы доказаны.  Остается добавить, что описать поступательное движение твердого тела можно,  задав уравнения движения любой из его точек.  Однако при решении  задач  динамики считается,  что имеющие вид :   

x_c = x_c(t) ;    y_c = y_c(t) ;     z_c = z_c(t)

 уравнения  поступательного  движения  тела описывают  движение  его центра тяжести.

1.2.2. Вращение тела относительно неподвижной оси Вращательным называется движение тела, при котором хотя бы две точки тела остаются неподвижными.

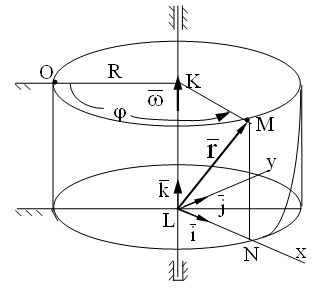        Прямая, проходящая через неподвижные точки  тела,  называется осью вращения.  При вращении тела все его точки движутся в плоскостях, перпендикулярных оси вращения, по окружностям, радиусы которых равны расстояниям точек до оси вращения.

      Вращательное движение тела  описывается  уравнением

вида    =  (t).

      Здесь   - величина двугранного угла  между проходящей  через  ось вращения   тела и  связанной с телом вращающейся   полуплоскостью  KMNL  и неподвижной координатной плоскостью. За положительное направление изменения угла принимают направление вращения против часовой стрелки.

Измерять  углы в механике принято в радианах. Нестандартной единицей  измерения  больших  углов поворота тел является число оборотов  -  N.   В  этом случае    = 2π N.

       Характеристиками  вращательного  движения  являются  угловая  скорость  тела  и  его  угловое  ускорение.