Вариант 3. Сложение вращений относительно параллельных осей

     Рассмотрим  на  следующем рисунке  тело,  участвующее в двух вращениях относительно параллельных осей.   Оно будет совершать плоское движение,  и ,  следовательно,  в каждый момент времени  мгновенно вращательное.    Выделив в движении тела его относительное вращение с угловой скоростью    относительно оси  О₁  и переносное вращение относительно неподвижной оси  Oz  с угловой скоростью  ,  найдем мгновенную угловую скорость и положение мгновенной оси вращения.

           Сделаем это сначала для случая, когда направления относительного и переносного вращений  совпадают.  Определим абсолютные скорости двух точек тела.  Легче всего это сделать для точек А и В,  находящихся на оси относительного и над осью переносного вращения.

   Покажем плоскость, в которой находятся  рассматриваемые точки, и  векторы скоростей  точек  А и В.    Векторы скоростей точек параллельны  между собой и перпендикулярны отрезку    АВ.

          Зная типовые случаи определения М.Ц.С., найдем положение мгновенной оси вращения и мгновенную угловую скорость вращения тела.

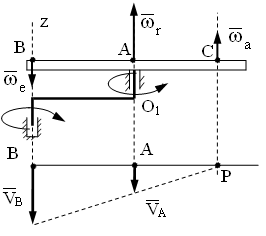          Сохранив для определенности,  что  > ,  изменим  на следующем рисунке  направление переносного вращения на противоположное. В этом случае скорости точек А и В  параллельны,  перпендикулярны АВ и направлены в одну сторону. 

 М.Ц.С.  находится   на продолжении отрезка АВ.   Угловая скорость  в мгновенном вращении равна  

 

   Из отношений скоростей  точек  А  и В  к  их  расстояниям  до  М.Ц.С.  

                        выясняем также, что

                           

             Если же ввести в рассмотрение векторы угловых скоростей в относительном и переносном вращении, то для каждого из рассмотренных случаев можно  записать  изложенное  выше  более  кратко.

И  в  заключение  сделаем  выводы. 

            Если тело участвует в двух вращениях относительно параллельных осей,  то:

         1.   В каждый момент,  кроме случая ,  когда  ,  движение тела  является мгновенно вращательным.  Мгновенная ось вращения находится в плоскости, проходящей через оси относительного и переносного вращений,  на расстояниях от этих осей,  обратно пропорциональных угловым скоростям в каждом из  вращений.

         2.  Мгновенная угловая скорость равна векторной сумме параллельных векторов угловых скоростей  в каждом из  вращений.

         3.   Абсолютное движение тела является плоским.

         4.   Случай, когда  ,  должен рассматриваться как особый случай поступательного движения тела.

 

Вариант 4. Пара вращений

         Этот случай  мы  и рассмотрим,  представив,  что на последнем рисунке скорости точек А и В   равны между собой.  В плоском  движении вариант,  когда были равны скорости двух точек отрезка,  нами рассматривался.  Но для случая,  когда векторы скоростей точек были не перпендикулярны к отрезку, соединяющему точки.   Тогда говорилось о мгновенно поступательном движении.   В случае сложения  вращений относительно  параллельных осей с равными  угловыми скоростями и при противоположном направлении вращений тело движется не мгновенно поступательно, а просто поступательно.   Здесь можно доказать,  что в любой момент движения тела равны  не только скорости, но и ускорения точек.  Случай этот называется - пара вращений.

       В действительности с такой парой вращений можно встретиться,   наблюдая  движение   кабины колеса обозрения.

При вращении колеса кабина поворачивается относительно оси подвески с той же угловой скоростью, что и колесо, но в противоположном направлении,   В результате -  кабина движется поступательно.

  В  технических  устройствах  иногда поступательное движение деталей механизмов получают,  заставляя эти детали участвовать в паре вращений.

     Вектор скорости поступательного движения тела, участвующего в паре вращений, определяется с помощью векторного произведения вектора угловой скорости переносного вращения на радиус-вектор,  соединяющий оси переносного и относительного вращений тела.

                                               =  .

         По аналогии  с  вектором-моментом  пары сил в статике вектор скорости   поступательного   движения   тела  в  паре  вращений  называют вектором-моментом  пары вращений.  Расстояние между осями в этом случае называют  плечом  пары вращений.

         Интересна аналогия между сложением векторов угловых скоростей  в кинематике  и сложением векторов  сил в статике. 

      И  в заключение к варианту 4.  Как вектор-момент пары сил в статике на чертеже всегда можно заменить парой сил,  так вектор скорости поступательного движения тела можно рассматривать как результат участия тела в паре вращений.   Последнее утверждение используем,  рассматривая  следующие  варианты сложения движений.