
- •Линейное программирование
- •1. Задача об использовании ресурсов: для изготовления 2-х видов конфет используется 4 вида ресурсов. Требуется составить такой план выпуска конфет, чтобы прибыль от их реализации была максимальной
- •Транспортная задача
- •Метод наименьших затрат
- •Метод потенциалов
- •Nb: Если все оценки неотрицательны, то решение – оптимально.
- •Элементы теории игр
- •Платежная матрица. Верхняя и нижняя цена игры
- •Решение игр смешанных стратегий
Модель – условный образ какого-либо объекта, приблизительно воссоздающий этот объект с помощью какого-либо языка.
Объектами ЭММ являются экономические процесса, а в качестве языка используется математический аппарат.
ЭММ – это математическое описание какого-либо экономического процесса или объекта.
Процесс математического моделирования состоит из 3 этапов: 1) постановка целей и задач исследования, проведение качественного описания объекта в виде модели; 2) количественное описание объекта в виде математической модели и проведение расчетов по ней; 3) анализ результатов и выбор решений.
Линейное программирование
1. Задача об использовании ресурсов: для изготовления 2-х видов конфет используется 4 вида ресурсов. Требуется составить такой план выпуска конфет, чтобы прибыль от их реализации была максимальной
Ресурсы |
Запас |
Расход |
4 х = (х1; х2) |
|
1-й вид |
2-й вид |
|
||
Патока |
18 |
1 |
3 |
х1 + 3*х2 18 |
Карамель |
16 |
2 |
1 |
1 2*х1 + х2 16 - система ограничений |
Шоколад |
5 |
- |
1 |
х2 5 |
Начинка |
21 |
3 |
- |
3*х1 21 |
Стоимость 1-й конфеты (руб.) |
2,00 |
3,00 |
3 F = 2*х1 + 3*х2 max |
|
ЭММ: найти такой план выпуска продукции (4), чтобы он удовлетворял системе (1) и условию (2), при котором функция (3) примет максимальное значение.
2. Задача на составление рациона: имеется 2 вида корма, содержащие витамины с1, с2, с3. Необходимо составить такой рацион с минимальной стоимостью, в котором бы содержание витаминов было бы не меньше нормы.
Витамины |
Необходимый минимум |
Количество витаминов |
4 х = (х1; х2) |
|
1-й корм |
2-й корм |
|
||
с1 |
9 |
3 |
1 |
3*х1 + х2 ≥ 9 |
с2 |
8 |
1 |
2 |
1 х1 + 2*х2 ≥ 8 - система ограничений |
с3 |
12 |
1 |
6 |
х1 + 6*х2 ≥ 12 |
|
|
|
|
|
Стоимость 1 кг корма (руб.) |
4,00 |
6,00 |
3 F = 4*х1 + 6*х2 min |
|
ЭММ: Найти такой рацион (4), чтобы он удовлетворял системе (1) и условию (2), при котором функция (3) примет минимальное значение.
3. Задача на раскрой материала: для изготовления брусьев длиной 1,2 м, 3м и 5 м на распил поступают 195 бревен длиной 6 м. Для изготовления 1 изделия требуется 2 бруса по 1,2 м, 1 брус на 3 м и 3 бруса на 5 м.
Способ распила |
Число полученных брусьев |
Xi ≥ 0; i = 1,4 |
||
1 вид (1,2 м) |
2 вид (3 м) |
3 вид (5 м) |
|
|
№ 1 (х1) |
- |
- |
1 |
2*х2 + 5*х4 = 2*х |
№ 2 (х2) |
2 |
1 |
- |
х2 + 2*х3 = х |
№ 3 (х3) |
5 |
- |
- |
х1 = 3*х |
№ 4 (х4) |
- |
2 |
- |
х1 + х2 + х3 + х4 = 195 |
Стоимость 1-й конфеты (руб.) |
2,00 |
3,00 |
|
|
NB: Во всех задачах ЛП система ограничений и целевая функция – линейные!
Общая постановка задач ЛП:
Дана система m линейных уравнений и неравенств с n переменных.
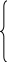
A11*X1 + A12*X2 + ... A1n*Xn B1 (2) F = C1*X1 + C2*X* + ... + Cn*Xn – целевая функция
A21*X1 + A22*X2 + ... A2n*Xn B2 (3) X = (X1, X2, ... Xn); (4) Xi ≥ 0; i = 1,n
(1) ...
Ak1*X1 + Ak2*X2 + ... Akn*Xn Bk
...
Am1*X1 + Am2*X2 + ... Amn*Xn Bm
Необходимо найти вектор (3), удовлетворяющий системе (1) и условиям (4), при котором функция (2) принимает оптимальное значение. Оптимальным решением (планом) называется решение (3) при котором функция (2) принимает оптимальное значение.
Если систем состоит только из неравенств, то говорят, что задача ЛП задана в стандартной форме; если только из уравнений, то, соответственно, в канонической форме.
Геометрический метод решения задач ЛП (можно решать задачи, содержащие две переменные).
Алгоритм решения:
1) Изобразить область, являющуюся решением системы ограничений с учетом условий неотрицательности.
2) Изобразит вектор, началом которого служит точка (0; 0), а концом – точка с координатами, соответствующими коэффициентам линейной функции.
3) Изобразить линию уровня перпендикулярно вектору.
4) Двигать линию уровня параллельно самой себе по направлению вектора для задачи на максимум, либо в противоположную – для задачи на минимум.
5) Точка выхода за границы области будет оптимальной.
Частные случаи графического решения:
а) Неограниченная функция: при перемещении линии уровня выхода за границы области не происходит. В задаче на максимум F +; в задаче на минимум F -. Оптимального решения не существует.
б) Альтернативный оптимизм: выход за границы области происходит на всем отрезке. Оптимальным решением будет являться любая точка на этом отрезке.
в) Отсутствие допустимых решений: область допустимых решений не образуется.
Симплексный метод
При решении геометрическим методом оптимальное решение (если оно существует) обязательно находится в угловой точке многоугольника решений или отрезка.
Симплексный метод проверяет одну за другой точки многоугольника решений и находит оптимальную, причем при переходе от одной точки в другой значение целевой функции улучшается.
Этапы симплексного метода:
1) способ определения какого-либо первоначального базисного решения;
2) правило перехода к лучшем решению;
3) критерий проверки найденного оптимального решения.
Решение: необходимо привести систему ограничения к каноническому виду, т.е. из неравенств получить уравнения. Если неравенство со знаком больше, то следует ввести дополнительную переменную со знаком минус, если со знаком меньше – то переменную со знаком плюс.
х1 + 3*х2 18 х2 5 3*х1 21 х1 ≥ 0; х2 ≥ 0 |
х1 + 3*х2 +х3 =18 2*х1 + х2 +х4 = 16 х2 +х5 = 5 3*х1 +х6 = 21 хi ≥ 0; i = 1.6 |
Процесс решения:
Шаг 1. Для нахождения первоначального базисного решения необходимо выбрать базисные (основные) переменные и свободные (неосновные переменные). В качестве основных переменных на данном этапе следует выбрать такие «m» переменных (m – число переменных), каждая из которых входит только в одно уравнение, и нет таких уравнений, в которые не входит ни одна переменная: основные – х3,х4,х5,х6; неосновные – х1,х2. Запишем систему уравнений, выразив основные переменные через свободные:
х3 = 18 – х1 – 3*х2
х4 = 16 – 2*х1 –х2
х5 = 5 – х2
х6 = 21 – 3*х1
Находим 1-е решение: несоновные переменные = 0, а основные находим из системы:
х1 = (0,0,18,16,5,21), F = 2*0 + 3*0 = 0
Проверяем оптимальность полученного решения. Для этого выразим линейную функцию через неосновные переменные: F = 2*х1 + 3*х2.
Если в задаче на максимум коэффициент линейной функции при неосновных переменных – положительный, то найденное решение неоптимально и для улучшения следует такую переменную перевести в основную.
Будем переводить в основные х2. Система уравнений накладывает ограничения на рост х2:
х3 = 18 – 3*х2 ≥ 0 х2 0
х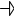 4
= 16 – х2 ≥ 0 х2
16
4
= 16 – х2 ≥ 0 х2
16
х5 = 5 – х2 ≥ 0 х2 5
Выбираем минимальный х2 = 5.
Для вводимой в базис переменной оценочное отношение составляется по правилу: в каждом уравнении свободный член делим на коэффициент перед этой переменной и выбираем наименьшее число.
Если делимое и делитель разных знаков, что частное берем со знаком плюс, если одно знака – по получаем .
х2 = min {18/3, 16/1, 5/1, } = 5
То уравнение, на котором достигается минимум, называется разрешающим, а соответственная переменная перейдет в неосновную.
х5 = 5 – х2
Шаг 2. Основные переменные – х2,х3,х4,х6. Новая система получается так: выражается новая основная переменная, остальные уравнения переписываются, причем вместо новой основной переменной вводится ее выражение из уравнения.
х2 = 5 – х5 х2 = 5 – х5
х3 = 18 – х1 – 3*(5 – х5) х3 = 3 – х1– х5
х 4 = 16 – 2х1 – (5 – х5) х4 = 11 – 2х1 + х5
х6 = 21 – 3х1 х6 = 21 – 3х1
х2 = (0,5,3,11,0,21)
F = 2*х1 + 3*х2 = 2*х1 + 3*(5 – х5) = 15 + 2*х1 – 3х5
х1 = min {, 3/1, 11/2, 21/3} = 3
х3 = 18 – х1 – 3*(5 – х5)
Шаг 3. Основные переменные: х1,х2,х4,х6
х1 = 3 – х3 + 3*х5 х1 = 3 – х3 + 3*х5
х2 = 5 – х3 х2 = 5 – х3
х4 = 11 – 2*(3 – х3 + 3*х5) х4 = 5 + 2*х3 - 5*х5)
х6 = 21 – 3*(3 – х3 + 3*х5) х6 = 12 + 3*х3 – 9х5
х3 = (3,5,0,5,012)
F = 2*х1 + 3*х2 = 2*(3 – х3 + 3х5) + 3*(5 – х5) = 21 – 2*х3 + 3*х5
х 5 = min {, 5, 1, 4/3} = 1
х4 = 5 + 2*х3 – 5*х5
Шаг 4. Основные переменные: х1,х2,х5,х6
х5 = 1 + 2/5*х3 – 1/5*х4
х5 = 1 + 2/5*х3 – 1/5*х4 х5 = 1 + 2/5*х3 – 1/5*х4
х 1 = 3 – х3 – 3*(1 + 2/5*х3 – 1/5*х4) х1 = 6 + 1/5*х3 – 3/5*х4
х2 = 5 – (1 + 2/5*х3 – 1/5*х4) х2 = 4 – 2/5*х3 + 1/5*х4
х6 = 3 + 3/5*х3 + 9/5*х4 х6 = 3 + 3/5*х3 + 9/5*х4
х4 = (6,4,0,0,1,3)
F = 2*х1 + 3*х2 = 2*(6 + 1/5*х3 – 3/5*ч4) + 3*(4 – 2/5*х3 + 1/5*х4) = 24 – 4/5*х3 – 3/5*х4
Оптимальное решение: х = (6,4,0,0,1,3)
F = 24 – 4/5*х3 – 3/5*х4
Признак оптимальности для задачи на максимум: коэффициенты всех переменных в линейной функции, выраженной через свободные переменные, - отрицательные; для задачи на минимум – положительные.
Неограниченность функции при решении симплексным методом проявляется, если все оценочные отношения для вводимой в базис отношения = . В таком случае оптимального решения нет.
Отсутствие допустимых решений выявляется, если какой-то из элементов – отрицательный и в соответствующем уравнении нет свободных переменных с положительным коэффициентом.
Альтернативный оптимум выражается в том, что минимальная функция не содержит одной из свободных переменных.

 2
х1 ≥ 0; х2 ≥ 0
2
х1 ≥ 0; х2 ≥ 0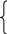 2
х1 ≥ 0; х2 ≥ 0
2
х1 ≥ 0; х2 ≥ 0
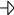 2*х1
+ х2
16
2*х1
+ х2
16