
- •1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
- •2) Понятие непрер кривой и области в r2
- •3) Предел послед точек в r2.
- •4) Определение ф-и от неск пер. График ф-и 2х пер.
- •5) Предел ф-и неск пер. Осн теоремы о пределах.
- •6) Непрер ф-и неск пер. Точки разрыва.
- •7) Непрер. Сложной ф-и.
- •8) Основные св-ва непрерывных ф-й
- •9) Равномерная непрер-ть функций 2х переменных
- •10) Частные производные ф-й нескольких переменных
- •11) Дифференцируемость функций нескольких переменных. Понятие дифференциала.
- •12) Необходимые условия дифференцируемости функции двух переменных
- •13) Достаточные условия дифференцируемости функции двух переменных
- •14) Дифференцируемость сложных функций нескольких переменных
- •15) Инвариантность формы дифференциала первого порядка.
- •16) Частные производные высших порядков.
- •17) Дифференциалы высших порядков.
- •18) Формула Тейлора.
- •19) Неявные функции. Дифференцируемость неявных функций.
- •20) Экстремумы функций двух переменных. Необходимое условие экстремума.
- •22) Достаточные условия экстремума для функции 2 переменных.
- •23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
- •26) Определение двойного интеграла. Условия существования двойного интеграла.
- •27) Основные свойства двойного интеграла
- •28)Понятие повторного интеграла для X-правильных областей.
- •29) Понятие повторного интеграла для y-правильных областей.
- •30) Способы вычисления двойного интеграла.
- •31) Замена переменной в двойном интеграле.
- •32) Двойной интеграл в полярных координат
- •36) Определение криволинейного интеграла по координатам (второго рода)
- •37) Свойства криволинейного интеграла второго рода.
- •38) Вычисление криволинейного интеграла второго рода
- •3 9) Криволинейный интеграл второго рода. Формула Грина.
- •40) Условия независимости криволинейного интеграла от путей интегрирования.
- •41) Условия полного дифференциала. Восстановление функции по ее полному дифференциалу.
- •42) Восстановление функции по ее полному дифференциалу
- •44) Криволинейные интегралы по длине дуги(первого рода).
20) Экстремумы функций двух переменных. Необходимое условие экстремума.
Опр1
Точка
называется точкой
(локального) максимума
функции
,
если существует такая окрестность
точки
,
что для каждой точки
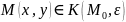 ,
отличной от
,
выполняется неравенство
,
отличной от
,
выполняется неравенство
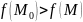 .
.
Опр2
Точка
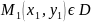 называется точкой
(локального) минимума
функции
,
если существует такая окрестность
называется точкой
(локального) минимума
функции
,
если существует такая окрестность
 точки
точки
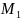 ,
что для каждой точки
,
что для каждой точки
 ,
отличной от
,
выполняется неравенство
,
отличной от
,
выполняется неравенство
 .
.
Т.
(необходимое условие экстремума)
Если
функция
в точке
имеет частные производные первого
порядка
 и
и
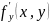 ,
то для того чтобы точка
была точкой экстремума данной функции,
необходимо, чтобы
,
то для того чтобы точка
была точкой экстремума данной функции,
необходимо, чтобы
 и
и
 .
.
22) Достаточные условия экстремума для функции 2 переменных.
Пусть M0(x0,y0) является критической точкой функции z=f(x,y).
Т.
(Достаточные условия экстремума)
Пусть функция z=f(x,y)
в некоторой окрестности критической
точки M0(x0,y0)
имеет непрерывные частные производные
до второго порядка включительно и пусть
 .
Тогда
.
Тогда
1)
если
 ,
то в точке M0(x0,y0)
функция z=f(x,y)
имеет экстремум, причем при условии
,
то в точке M0(x0,y0)
функция z=f(x,y)
имеет экстремум, причем при условии
 точка M0
будет точкой минимума, а при
точка M0
будет точкой минимума, а при
 точка M0
будет точкой максимума;
точка M0
будет точкой максимума;
2)
если
 ,
то в точке M0
нет экстремума;
,
то в точке M0
нет экстремума;
3)
если
 ,
вопрос об экстремуме остается открытым,
т.е. необходимы дополнительные исследования
с привлечением производных более
высокого порядка.
,
вопрос об экстремуме остается открытым,
т.е. необходимы дополнительные исследования
с привлечением производных более
высокого порядка.
Замеч. Исследуя функцию z=f(x,y) на экстремум с помощью теоремы, мы оставляем в стороне те критические точки, при которых хотя бы одна из частных производных первого порядка не существует. Поэтом при решении задач на экстремум функций, необходимо исследовать (не прибегая к теореме) рассматриваемую функцию и в критических точках указанного типа.
23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
Пусть
D
– замкнут и огранич. обл. на R².
И пусть в D
опред. ф-ция z=f(x,y).
Предположим, что f(x,y)
непрерыв. в D.
Тогда согласно 2-й Т.Вейерштрасса она
достиг. наим. и наиб. значение, т.е.
 (
( ;
;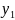 ):
f(
)=
sup
f(M);
):
f(
)=
sup
f(M);
 (
( ;
; ):
f(
):
f(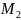 )=
inf
f(M);
)=
inf
f(M);
Здесь возможны два случаю: 1) наиб. и наим. значение ф-ия достигает во внутр. точках обл. D. 2) Но т.к. обл. явл. замкнутой, то может оказ., что она достиг. наим/наиб. знач. в гранич. точках.
Ясно, что если ф-ия достиг. наиб/наим. знач. во внутр. точках обл. D, то эти точки обязательно будут критическими. Поэтому, для нахожд. наим/наиб. значения ф-ии f в замк. и огранич. обл. D можно использовать след. правило!!
Сначала находим все критические точки ф-ии f в обл D.
Исследуем ф-ию f в этих критических точках на экстемум и находим
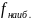 и
и
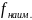 в нутрии D.
в нутрии D.Находим и на границе Г области D.
Выбираем самое наиб. из всех найденных знач. f. Это и будет в замкнутой обл. D.
Выбираем из всех найденных знач. f самое наим. Это и будет в замкнутой обл. D.
26) Определение двойного интеграла. Условия существования двойного интеграла.
Опр. Говорят, что многоугольник Q вписан в фигуру D, если каждая точка этого многоугольника принадлежит фигуре D. Будем говорить, что Q описан вокруг D, если все точки этой фигуры и ее границы принадлежат данному многоугольнику.
Обозначим
через {Sk}множество
площадей вписанных в D
многоугольников, а через {Sn}
– множество площадей описанных вокруг
D
многоугольников. Ясно, что первое
множество имеет точную верхнюю грань
(обозначим ее через
 ),
а второе – точную нижнюю (
),
а второе – точную нижнюю (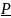 ).
).
Опр.
Плоская фигура D
называется квадрируемой, если
=
.
Число
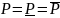 называется площадью фигуры D.
называется площадью фигуры D.
Опр. Кривую Г называют кривой площади нуль, если для любого ε>0 найдется многоугольник, содержащий все точки Г и имеющий площадь меньшую ε.
Т. Для того, чтобы плоская фигура D была квадрируемой необходимо и достаточно, чтобы ее граница Г была кривой площади нуль.
Пусть
D
– замкнутая ограниченная область,
имеющая границу Г площади нуль. Допустим,
что в области D
определена некоторая функция Z=f(x,y),
которая является ограниченной в этой
области. Разобьем D
при помощи конечного числа произвольных
кривых площади нуль на конечное число
n
частичных областей D1,…,
Dn
(без общих внутренних точек). Заметим,
что каждая Di
будет квадрируемой. Обозначим площадь
Di
через Δσi.
В каждой частичной области выберем
произвольную точку Pi(ξi,ŋi)
и составим сумму
 (1) которую будем называть интегральной
суммой для функции f(x,y)
в области D.
Ясно, что меняя сеть разбиения области
D
и способ выбора точек Pi
в частичных областях, можно составлять
бесконечно много интегральных сумм
вида (1), вообще говоря, различных между
собой. Обозначим через 𝝀
наибольший из диаметров частичных
областей Di.
(1) которую будем называть интегральной
суммой для функции f(x,y)
в области D.
Ясно, что меняя сеть разбиения области
D
и способ выбора точек Pi
в частичных областях, можно составлять
бесконечно много интегральных сумм
вида (1), вообще говоря, различных между
собой. Обозначим через 𝝀
наибольший из диаметров частичных
областей Di.
Опр.
Число J
называется пределом интегральных сумм
(1) при ,если для любого ε>0 существует
такое δ>0, что при 𝝀<δ
выполняется неравенство
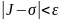 ,
независимо ни от способа разбиения
области D
на Di,
ни от выбора точек Pi(ξi,ŋi)
в этих областях.
,
независимо ни от способа разбиения
области D
на Di,
ни от выбора точек Pi(ξi,ŋi)
в этих областях.
 .
.
Опр.
Функция f(x,y)
называется интегрируемой в области D,
если существует конкретный предел J
интегральных сумм (1) этой функции при
 .
При этом предел J
называется двойным интегралом от функции
f(x,y)
по области D
и обозначается одним из символов:
.
При этом предел J
называется двойным интегралом от функции
f(x,y)
по области D
и обозначается одним из символов:
 или
или
 .
Таким образом
.
Таким образом
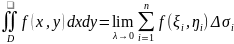 .
D
называют областью интегрирования,
f(x,y)
– подынтегральной функцией,
.
D
называют областью интегрирования,
f(x,y)
– подынтегральной функцией, - элементом площади,
- элементом площади,
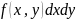 - подынтегральным выражением. Зам.
Для того, чтобы функция была интегрируемой,
необходимо, чтобы она была ограниченной
в данной области. Однако, ограниченность
функции не является достаточным условием.
- подынтегральным выражением. Зам.
Для того, чтобы функция была интегрируемой,
необходимо, чтобы она была ограниченной
в данной области. Однако, ограниченность
функции не является достаточным условием.
Пусть
функция Z=f(x,y)
является ограниченной в D,
т.е.
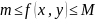 ,
где
,
где
 .
Рассмотрим нижние и верхние интегральные
суммы
.
Рассмотрим нижние и верхние интегральные
суммы
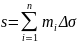 и
и
 ,
где
,
где
 ,
,
 означают, соответственно, точную нижнюю
и верхнюю границы значений функции
f(x,y)
в частичной области.
означают, соответственно, точную нижнюю
и верхнюю границы значений функции
f(x,y)
в частичной области.
Т.
Для того, чтобы ограниченная в области
D
функция f(x,y)
была интегрируемой в этой области,
необходимо и достаточно, чтобы
 .
.
Т. Если функция f(x,y) непрерывна в области D, то она в этой области интегрируема.
