
- •1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
- •2) Понятие непрер кривой и области в r2
- •3) Предел послед точек в r2.
- •4) Определение ф-и от неск пер. График ф-и 2х пер.
- •5) Предел ф-и неск пер. Осн теоремы о пределах.
- •6) Непрер ф-и неск пер. Точки разрыва.
- •7) Непрер. Сложной ф-и.
- •8) Основные св-ва непрерывных ф-й
- •9) Равномерная непрер-ть функций 2х переменных
- •10) Частные производные ф-й нескольких переменных
- •11) Дифференцируемость функций нескольких переменных. Понятие дифференциала.
- •12) Необходимые условия дифференцируемости функции двух переменных
- •13) Достаточные условия дифференцируемости функции двух переменных
- •14) Дифференцируемость сложных функций нескольких переменных
- •15) Инвариантность формы дифференциала первого порядка.
- •16) Частные производные высших порядков.
- •17) Дифференциалы высших порядков.
- •18) Формула Тейлора.
- •19) Неявные функции. Дифференцируемость неявных функций.
- •20) Экстремумы функций двух переменных. Необходимое условие экстремума.
- •22) Достаточные условия экстремума для функции 2 переменных.
- •23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
- •26) Определение двойного интеграла. Условия существования двойного интеграла.
- •27) Основные свойства двойного интеграла
- •28)Понятие повторного интеграла для X-правильных областей.
- •29) Понятие повторного интеграла для y-правильных областей.
- •30) Способы вычисления двойного интеграла.
- •31) Замена переменной в двойном интеграле.
- •32) Двойной интеграл в полярных координат
- •36) Определение криволинейного интеграла по координатам (второго рода)
- •37) Свойства криволинейного интеграла второго рода.
- •38) Вычисление криволинейного интеграла второго рода
- •3 9) Криволинейный интеграл второго рода. Формула Грина.
- •40) Условия независимости криволинейного интеграла от путей интегрирования.
- •41) Условия полного дифференциала. Восстановление функции по ее полному дифференциалу.
- •42) Восстановление функции по ее полному дифференциалу
- •44) Криволинейные интегралы по длине дуги(первого рода).
1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
Опр. Всякий набор из n действит чисел х1, x2,…,xn будем наз n-мерной точкой. А сами числа х1, х2,…,хn будем наз корд этой т, обозн А(х1, x2,…,xn) или В(х1, x2,…,xn).
Опр. Множ-во всевозмож n-мерных точек наз n-мерным арифм пр-вом или n-мерным координатным пр-вом.
Опр.
n-мерное
арифм пр-во наз n-мерным
евклидовым пр-вом,
если ∀2х
точек А(х1,
x2,…,xn)
и В(х1,
x2,…,xn)
определено расстояние ρ, по формуле
ρ(А,В)= (1)
Обозн Rn,
n∈N.
(1)
Обозн Rn,
n∈N.
Опр. Множ-во всех т М(х1, x2,…,xn)∈Rn, удовл нер-ву: ρ(M0,M)<ℰ или (x1-x10)2+(x2-x20)2+…+(xn-xn0)2<ℰ2 наз. n-мерным (открытым) шаром, с центром в т М0 и радиусом ℰ, ℰ>0. Обозн K(M0, ℰ).
Опр.
Множ-во
точек М∈Rn,
удовл нер-ву ρ(М0,M)≤ℰ
наз n-мерным
замкнутым шаром
с центром в т М0
и радиусом ℰ, ℰ>0, обозн
 (М0,
ℰ).
(М0,
ℰ).
Опр. Множ-во всех т М(х1, x2,…,xn)∈Rn, удовл рав-ву ρ(М0,M)=ℰ или (x1-x10)0+(x2-x20)2+…+(xn-xn0)2=ℰ2 , будем наз n-мерной сферой, с центром в т М0 и радиусом ℰ, ℰ>0. Обозн S(M0, ℰ).
Опр.
n-мерным
(открытым) параллепипедом,
с центром в т М0
будем наз множ точек М(х1,
x2,…,xn)∈Rn,
кот удовл системе нер-в:
 обозн П(М0,
ℰ). d=min{d1,d2,…,dn},
di∈R+
обозн П(М0,
ℰ). d=min{d1,d2,…,dn},
di∈R+
Опр.
Множ
т М∈Rn,
корд кот удовл сист
 наз n-мерным
замкнутым параллепипедом (di∈R+).
наз n-мерным
замкнутым параллепипедом (di∈R+).
Опр. Окрестностью точки М0 наз. всякий открытый шар, с центром в этой т.
Опр. Пусть R2 –евкл. пл-ть, т.е 2-мерное евкл. пр-во. Пусть Е⊂R2 –произв. множ. точек. и пусть т. М0∈E наз. внутренней точкой этого множ-ва, если ∃К(М0,ℰ)⊂E. Др словами т М0 наз внутр т этого мн-ва, если эта т ∈ данному мн-ву с нек окрестностью.
Опр. Т. М0 наз. предельной т. мн-ва Е, если в любой окр К(М0,ℰ) данной точки сущ. хотя бы 1 т М∈E. Легко док-ть что опр предельной т эквивалентно след:
Опр. Т. М0 наз предельной т мн-ва Е, если в любой окр этой т содерж бесчисл множ точек этого мн-ва Е.
Опр. Окрестностью т М0 на R2 наз всякий открытый круг К(М0,ℰ), с центром в этой т. напр R2-окр для М0.
Опр. Т. М0 наз граничной т мн-ва Е, если в любой окр К(М0,ℰ) этой т имеются т как принадл Е так и не принадл Е.
Замеч. Сама предельная т мн-ва Е может как∈так и не ∈Е.
Опр. Множ Е наз открытым, если все его т явл внутренними, напр всякий откр круг К(М0,q).
Опр. Множ Е наз замкнутым, если оно содержит все свои предельные точки
Опр. Множ всех гранич точек мн-ва Е наз его границей.
Утв. Множ Е замкнуто т.и.т.т. когда оно содержит свою границу. Всякий замкнутый круг явл примером замкнутого множ.
2) Понятие непрер кривой и области в r2
Опр.
Непрер
кривой
L
в пр-ве R2xy
наз мн-во точек М(х,у), корд-ты которых
представляют собой непрерывные функции
некоторого переменного:
 (1),
где φ(t)
и ψ(t)
– непрер ф-и на [α,β].
(1),
где φ(t)
и ψ(t)
– непрер ф-и на [α,β].
Опр.
Кривая
L
наз замкнутой,
если
 в прот случае кривая L
наз разомкнутой.
В т А(φ(α),ψ(α))-начало кривой L,
В т В(φ(β),ψ(β))-конец этой кривой. Обозн
L=AB.
в прот случае кривая L
наз разомкнутой.
В т А(φ(α),ψ(α))-начало кривой L,
В т В(φ(β),ψ(β))-конец этой кривой. Обозн
L=AB.
Опр. Множ E на R2 наз связным, если ∀A,B∈E можно соед непрер кривой L=AB, причём L⊂E, напр всякий откр круг К(М0,ℰ).
Опр. Всякое откр и связное мн-во на R2 наз областью или откр областью.
3) Предел послед точек в r2.
Опр.
Пусть
дана послед точек М1(х1,
у1),
М2(х2,
у2),…,Мn(xn,
yn)
(1) кратко {Mn(xn,
yn)}.
Говорят что точка М0(х0,
у0)
явл пределом
последовательности
{Mn(xn,
yn)},
если ∀ℰ>0 ∃N1,
что ∀n>N1
вып нер-во:
 Др словами
Др словами
 n=M0
или MnàM0,
при nà∞.
Т.о
n=M0ó
n=M0
или MnàM0,
при nà∞.
Т.о
n=M0ó n,M0)=0.
n,M0)=0.
Т1.
Для
того чтобы
n=M0
(*)
необх и дост, чтобы
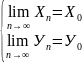 (**)
Др словами: сх-ть послед-ти точек на евкл
пл-ти равносильна покоординатной сх-ти
этих точек, т.е (*)ó(**).
(**)
Др словами: сх-ть послед-ти точек на евкл
пл-ти равносильна покоординатной сх-ти
этих точек, т.е (*)ó(**).
