- •1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
- •2) Понятие непрер кривой и области в r2
- •3) Предел послед точек в r2.
- •4) Определение ф-и от неск пер. График ф-и 2х пер.
- •5) Предел ф-и неск пер. Осн теоремы о пределах.
- •6) Непрер ф-и неск пер. Точки разрыва.
- •7) Непрер. Сложной ф-и.
- •8) Основные св-ва непрерывных ф-й
- •9) Равномерная непрер-ть функций 2х переменных
- •10) Частные производные ф-й нескольких переменных
- •11) Дифференцируемость функций нескольких переменных. Понятие дифференциала.
- •12) Необходимые условия дифференцируемости функции двух переменных
- •13) Достаточные условия дифференцируемости функции двух переменных
- •14) Дифференцируемость сложных функций нескольких переменных
- •15) Инвариантность формы дифференциала первого порядка.
- •16) Частные производные высших порядков.
- •17) Дифференциалы высших порядков.
- •18) Формула Тейлора.
- •19) Неявные функции. Дифференцируемость неявных функций.
- •20) Экстремумы функций двух переменных. Необходимое условие экстремума.
- •22) Достаточные условия экстремума для функции 2 переменных.
- •23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
- •26) Определение двойного интеграла. Условия существования двойного интеграла.
- •27) Основные свойства двойного интеграла
- •28)Понятие повторного интеграла для X-правильных областей.
- •29) Понятие повторного интеграла для y-правильных областей.
- •30) Способы вычисления двойного интеграла.
- •31) Замена переменной в двойном интеграле.
- •32) Двойной интеграл в полярных координат
- •36) Определение криволинейного интеграла по координатам (второго рода)
- •37) Свойства криволинейного интеграла второго рода.
- •38) Вычисление криволинейного интеграла второго рода
- •3 9) Криволинейный интеграл второго рода. Формула Грина.
- •40) Условия независимости криволинейного интеграла от путей интегрирования.
- •41) Условия полного дифференциала. Восстановление функции по ее полному дифференциалу.
- •42) Восстановление функции по ее полному дифференциалу
- •44) Криволинейные интегралы по длине дуги(первого рода).
17) Дифференциалы высших порядков.
Напомним,
что если функция Z=f(x,y)диффер.
в области D,
то дифференциал первого порядка этой
ф-ии в некоторой точке M(x,y)E
D
представляется в виде
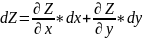 ,
где dx=
,
где dx=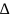 x
, dy
=
y
– произвольные приращения независимых
переменных x
и y.
Если зафиксировать приращения
x
и
y
то дифференциал dZ
будет функцией переменных x
и y
в области D.Следовательно
можно рассмотреть понятие дифференциала
от ф-ии dZ.
x
, dy
=
y
– произвольные приращения независимых
переменных x
и y.
Если зафиксировать приращения
x
и
y
то дифференциал dZ
будет функцией переменных x
и y
в области D.Следовательно
можно рассмотреть понятие дифференциала
от ф-ии dZ.
Опр.
Дифференциал
от дифференциала первого порядка dZ
ф-ии Z=f(x,y)
в точке M(x,y),
соответсвующего приращения
x,
y
называется дифференциалом второго
порядка ф-ии Z=f(x,y)
в этой точке и обозначается символом
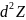 т.е.
=d(dZ).Теперь
пользуясь правилами дифференцирования
и учитывая, что приращения dx=
dy
=
здесь постоянные величины, найдём
выражение для
считая что dZ
– дифференцируемая ф-я в т.M(x,y).
т.е.
=d(dZ).Теперь
пользуясь правилами дифференцирования
и учитывая, что приращения dx=
dy
=
здесь постоянные величины, найдём
выражение для
считая что dZ
– дифференцируемая ф-я в т.M(x,y).
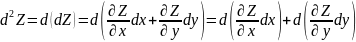 =
=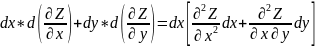 +
+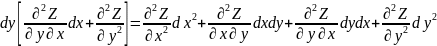 =
=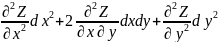 .Итак
,
.Итак
,
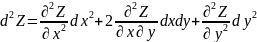 .
.
Опр.
Дифференциал от дифференциала (n-1)-го
порядка ф-ии Z=f(x,y)
в т.M(x,y)
называется дифференциалом n-го
порядка ф-ии Z=f(x,y)
в этой точкеи обозначается символом
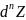 .Таким
образом
.Таким
образом
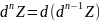 .
.
Если
ф-я Z=f(x,y)
n
раз дифференцируема в данной т.
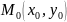 то с помощью метода мат. индукции можно
показать что
в этой точке можно выразить символической
формулой:
то с помощью метода мат. индукции можно
показать что
в этой точке можно выразить символической
формулой:
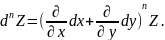 Отсюда применив формулу бинома Ньютона
получаем формулу для вычисления :
:
Отсюда применив формулу бинома Ньютона
получаем формулу для вычисления :
:
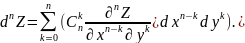
18) Формула Тейлора.
Т.
Пусть
ф-я Z=f(x,y)
определена в некоторой
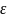 окрестности K(
окрестности K(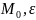 )
точки
и n+1
дифференцируема в этой окрестности.
Тогда полное приращение
)
точки
и n+1
дифференцируема в этой окрестности.
Тогда полное приращение
 =f(M)
– f(
=f(M)
– f(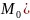 этой ф-ии в т.
этой ф-ии в т.
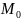 для любой точки
для любой точки
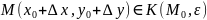 может быть представлена в виде (1):
может быть представлена в виде (1):
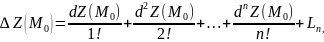 где
где
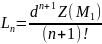 а
а
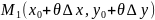 – некоторая точка из данной
окрестности т.
– некоторая точка из данной
окрестности т.

19) Неявные функции. Дифференцируемость неявных функций.
Опр1
Если каждому значению переменной x
из некоторого множества D
ставится в соответствие определенное
число y
так, что упорядоченная пара (x,y)
удовлетворяет уравнению вида
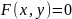 ,
то говорят, что y
является неявной функцией переменной
x
, заданной на множестве D
посредством функционального уравнения
.
,
то говорят, что y
является неявной функцией переменной
x
, заданной на множестве D
посредством функционального уравнения
.
Т1
Пусть
относительно функции
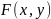 выполняются следующие условия:
выполняются следующие условия:
определена и непрерывна вместе со своими частными производными
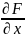 и
и
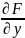 в некоторой -окрестности
в некоторой -окрестности
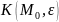 точки
.
точки
.В точки имеет место равенство
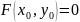 .
.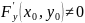 .
.
Тогда
уравнение
определяет единственную дифференцируемую
в некоторой -окрестности
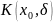 точки
неявную функцию
точки
неявную функцию
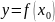 ,
причем производная этой неявной функции
вычисляется по формуле:
,
причем производная этой неявной функции
вычисляется по формуле:
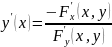 .
.
Опр2
Если
каждой паре
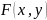 из некоторого множества G
из некоторого множества G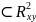 ставится в соответствие единственное
число z
так, что упорядоченная тройка
ставится в соответствие единственное
число z
так, что упорядоченная тройка
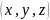 удовлетворяет функциональному уравнению
удовлетворяет функциональному уравнению
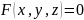 ,
то говорят, что на G
задана неявно функция вида
,
то говорят, что на G
задана неявно функция вида
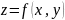 посредством функционального уравнения
.
посредством функционального уравнения
.
Т2
Пусть относительно функции
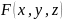 выполняются следующие условия:
выполняются следующие условия:
определена и непрерывна вместе со своими частными производными
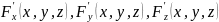 в некоторой - окрестности
точки
в некоторой - окрестности
точки
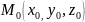
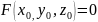
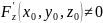
Тогда
уравнение
определяет единственную дифференцируемую
в некоторой окрестности
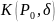 точки
точки
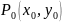 неявную функцию вида
,
которая удовлетворяет равенству
неявную функцию вида
,
которая удовлетворяет равенству
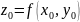 ,
причем частные производные функции
,
в указанной окрестности
определяются по формулам:
,
причем частные производные функции
,
в указанной окрестности
определяются по формулам: