
- •1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
- •2) Понятие непрер кривой и области в r2
- •3) Предел послед точек в r2.
- •4) Определение ф-и от неск пер. График ф-и 2х пер.
- •5) Предел ф-и неск пер. Осн теоремы о пределах.
- •6) Непрер ф-и неск пер. Точки разрыва.
- •7) Непрер. Сложной ф-и.
- •8) Основные св-ва непрерывных ф-й
- •9) Равномерная непрер-ть функций 2х переменных
- •10) Частные производные ф-й нескольких переменных
- •11) Дифференцируемость функций нескольких переменных. Понятие дифференциала.
- •12) Необходимые условия дифференцируемости функции двух переменных
- •13) Достаточные условия дифференцируемости функции двух переменных
- •14) Дифференцируемость сложных функций нескольких переменных
- •15) Инвариантность формы дифференциала первого порядка.
- •16) Частные производные высших порядков.
- •17) Дифференциалы высших порядков.
- •18) Формула Тейлора.
- •19) Неявные функции. Дифференцируемость неявных функций.
- •20) Экстремумы функций двух переменных. Необходимое условие экстремума.
- •22) Достаточные условия экстремума для функции 2 переменных.
- •23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
- •26) Определение двойного интеграла. Условия существования двойного интеграла.
- •27) Основные свойства двойного интеграла
- •28)Понятие повторного интеграла для X-правильных областей.
- •29) Понятие повторного интеграла для y-правильных областей.
- •30) Способы вычисления двойного интеграла.
- •31) Замена переменной в двойном интеграле.
- •32) Двойной интеграл в полярных координат
- •36) Определение криволинейного интеграла по координатам (второго рода)
- •37) Свойства криволинейного интеграла второго рода.
- •38) Вычисление криволинейного интеграла второго рода
- •3 9) Криволинейный интеграл второго рода. Формула Грина.
- •40) Условия независимости криволинейного интеграла от путей интегрирования.
- •41) Условия полного дифференциала. Восстановление функции по ее полному дифференциалу.
- •42) Восстановление функции по ее полному дифференциалу
- •44) Криволинейные интегралы по длине дуги(первого рода).
42) Восстановление функции по ее полному дифференциалу
Т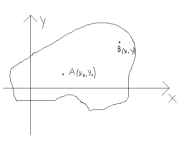 еорема1:
Пусть
P(x,y)
и Q(x,y)
определены и непрерывны в некоторой
односвязной области D
вместе со своими производными
еорема1:
Пусть
P(x,y)
и Q(x,y)
определены и непрерывны в некоторой
односвязной области D
вместе со своими производными
 и
и
 .
Тогда, для того чтобы выражение P(x,y)dx
+ Q(x,y)dyбыло
полным дифференциалом некоторой функции
U(x,y)
области Dнеобходимо
и достаточно, чтобы
.
Тогда, для того чтобы выражение P(x,y)dx
+ Q(x,y)dyбыло
полным дифференциалом некоторой функции
U(x,y)
области Dнеобходимо
и достаточно, чтобы

ПустьA(x0,y0) – фиксированная точка из D.B(x,y) – произвольная точка из D.
Если
выполняется условие теоремы1, то
 .
Ее можно восстановить по формуле:
.
Ее можно восстановить по формуле:
 (1),
с – произвольная постоянная.
(1),
с – произвольная постоянная.
З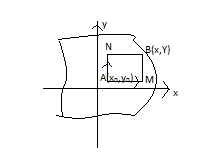 амеч:Ясно,
что при выполнении условий теоремы1
криволинейный интеграл правой части
формулы (1) не зависит от пути интегрирования
в области D.
Поэтому в качестве пути интегрирования,
можно выбрать любой путь, который будет
удобен для вычисления интеграла.В
качестве пути интегрирования для
интеграла из (1) берут либо L1=AMB
либо L2=ANB.
амеч:Ясно,
что при выполнении условий теоремы1
криволинейный интеграл правой части
формулы (1) не зависит от пути интегрирования
в области D.
Поэтому в качестве пути интегрирования,
можно выбрать любой путь, который будет
удобен для вычисления интеграла.В
качестве пути интегрирования для
интеграла из (1) берут либо L1=AMB
либо L2=ANB.

 ;
dy=0, dx=dx;
;
dy=0, dx=dx;
 ;
dx=0, dy=dy
;
dx=0, dy=dy

Аналогично можно получить вторую формулу для направления L2=ANB
44) Криволинейные интегралы по длине дуги(первого рода).
L=AB-Спрямляемая кривая на xOy.
z=f(M)
или z=f(x,y)-определена
на кривой L,т.е.
 M(x,y)
M(x,y) L
L
 f(M)
f(M)
Разобьём кривую L на n частей
A=
,
,
,…, =B
=B
На
каждой дуге
 (k=1,2,…,n)
выберем произвольным образом
(k=1,2,…,n)
выберем произвольным образом
 (
( ,
, ),(k=1,2,…,n)
),(k=1,2,…,n)
 =
= *
* -длина
дуги
-длина
дуги
Меняя
способ разбиения L
и выбор
можно составлять сколько угодно сумм
вида
.
Обозначим их

Обычно сумма вида называется интегральной суммой f(x,y),заданной на кривой L=AB.
Обозначим
через
 =max
=max ,
1
,
1 k
n
k
n
Опр1.
число
 называется пределом
при
называется пределом
при
 0,если
для
0,если
для
 0,
0,
 0,что
как только
0,что
как только
 |
-
|
|
-
| независимо ни от способа разбиения
кривой L
на частичные дуги,ни от выбора
независимо ни от способа разбиения
кривой L
на частичные дуги,ни от выбора

=
Опр2.
Если
конечный предел
интегральных сумм
при
0,то
называется криволинейным интегралом
от f(x,y)
по длине дуги
 .
.
= d
d
Вычисление криволинейного интеграла 1-го рода:
Пусть L-гладкая простая кривая
(1)

Теорема1: Если z=f(x,y) непрерывна на гладкой кривой ,заданной параметрически системой (1),то = d ,причём
=
d
= dt
(2)
dt
(2)
Замечание:
Если L
явл-ся кусочно гладкой,т.е. L= ,где
,где
 -гладкие,то
d
=
-гладкие,то
d
=
