6. Кластерный анализ

Кластерный анализ является методом объединения индивидуумов или объектов в группы, однородные по переменным, определенным исследователем. Число и характеристики выделяемых с помощью кластерного анализа групп обычно не известны до начала анализа. Таким образом, этот метод выступает и как средство углубления теоретического знания об изучаемом объекте, и как средство выделения групп, имеющее прикладной, практический характер.

На практике метод кластерного анализа часто используют для сегментации рынков, эмпирической классификации объектов. При проведении кластерного анализа исследователю необходимо помнить о следующем:

• большинство методов кластерного анализа – это сравнительно простые процедуры, не имеющие сложного статистического обоснования;

• различные методы кластерного анализа могут давать разные решения на основании одного и того же набора данных.

В силу этих особенностей метод кластерного анализа может считаться эвристическим методом поиска, требующим не только соблюдения статистических правил поиска решений и вывода заключений, но и глубокого теоретического понимания изучаемого объекта.

Критическим моментом при использовании метода кластерного анализа является определение показателей сходства. Чтобы сгруппировать объекты, необходим некоторый показатель сходства или различия. Схожие объекты группируются вместе, а те, что отстоят от них, попадают в другие кластеры. Например, каждый респондент в нашем исследовании может быть охарактеризован 26 переменными, отражающими его склонность ассоциировать творчество с какими-либо смыслами. Задача кластерного анализа заключается в том, чтобы выделить группы студентов, обладающие приблизительно сходными ассоциациями. Но для проведения такого анализа нужно выбрать способ определения похожести студентов по их характеристикам.

Среди наиболее часто используемых в кластерном анализе показателей можно перечислить следующие:

1. меры расстояния,

2. меры связи.

Меры расстояния. Наиболее популярный показатель – Евклидово расстояние, хорошо знакомое всем по школьным урокам геометрии. В Евклидовом пространстве расстояние между точками измеряется согласно теореме Пифагора, обобщенной на многомерное пространство. Евклидово расстояние вычисляется следующим образом:

расстояние (x,y) = { Σ _i (x_i - y_i)² }^1/2 .

Квадрат евклидова расстояния. Иногда, чтобы придать больший вес более отдаленным друг от друга объектам, возводят в квадрат стандартное евклидово расстояние.

Расстояние городских кварталов (манхэттенское расстояние). Расстояние определяется просто как средняя разность по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного евклидового расстояния. В отличие от квадрата евклидова расстояния, для данной меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле

расстояние (x,y) = Σ _i |x_i - y_i| .

Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они не совпадают по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

расстояние (x,y) = максимум |x_i - y_i|

Предположим, что каждого респондента характеризуют всего две переменные – ассоциирование творчества с вдохновением и престижем. Первый студент имеет показатели 6 и 5 по этим переменным соответственно. Второй – 3 и 7. В этом случае евклидово расстояние между студентами составит (6-3) ² + (5-7) ² =11, квадрат евклидова расстояния составит 121, манхэттенское расстояние – 5, расстояние Чебышева – 3.

Если переменные измерены в различных единицах, то единица измерения влияет на результат кластеризации. В этих случаях перед кластеризацией мы должны нормализовать данные, изменив шкалу измерения каждой переменной на стандартную Z-шкалу (среднее этой шкалы равно нулю, стандартное отклонение равно единице).

Меры связи. Применяются для установления схожести между объектами при использовании двоичных (0,1) переменных. Предположим, мы хотим определить сходство респондентов по ответам на вопрос: «Какие техники творчества Вам знакомы?» с номинальной шкалой.

Один из показателей простого соответствия, или коэффициент ассоциации s, может быть рассчитан по формуле

s = a/d,

где a – число совпавших ответов, d – число всех ответов.

Процент несогласия. Это расстояние вычисляется по формуле, обратной коэффициенту ассоциации:

расстояние (x,y) = (количество x_i ≠ y_i)/ i .

Методы кластеризации

Существуют два подхода к формированию кластеров – иерархический и неиерархический.

Иерархическая кластеризация (снизу вверх) предполагает последовательное пошаговое объединение объектов в кластеры. На каждом шаге процесса кластеризации объединяются в один кластер наиболее близко расположенные объекты. Постепенно кластеры растут, укрупняются, «впитывая в себя» близкие объекты, соединяясь с близко расположенными кластерами. В конечном счете образуется один большой кластер, вмещающий в себя все объекты. Графически процесс роста и объединения кластеров можно наблюдать на древовидной диаграмме (рис. 6.1).

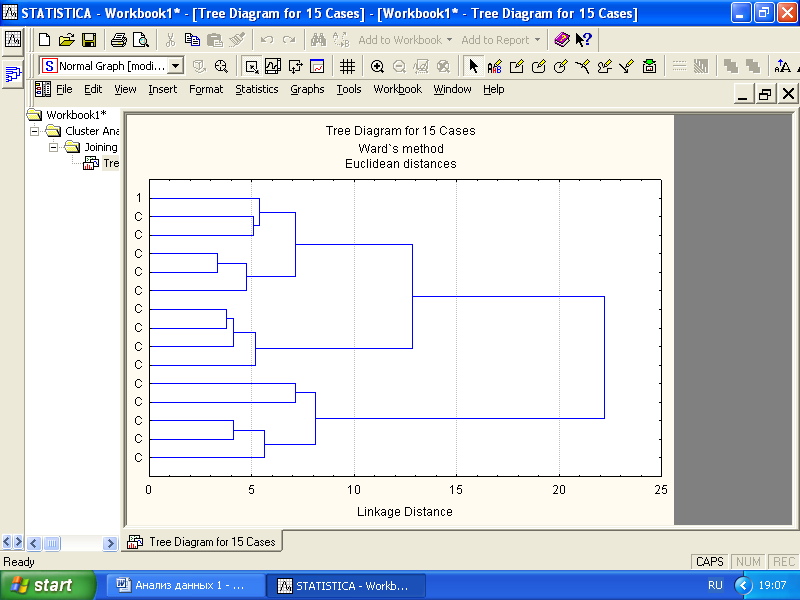
Рис. 6.1. Древовидная дендрограмма иерархической кластеризации

Соединение горизонтальных линий линиями-«перемычками» означает объединение случаев в один кластер. По горизонтальной оси откладываются расстояния между объектами или центрами кластеров. Линия-«перемычка» определяет размер вновь образованного кластера, при котором стало возможным объединение. Так, при росте критерия кластеризации (Linkage Distance) до 22 два самых крупных кластера объединяются в один конечный. До этого еще два кластера объединились на расстоянии 13.

Преимущество иерархической кластеризации заключается в простоте интерпретации результатов. Недостаток иерархической кластеризации состоит в том, что она является сравнительно нестабильной и ненадежной. Первое объединение объектов, которое может основываться на особенностях критерия кластеризации, предопределит судьбу дальнейшего процесса.

При проведении иерархической кластеризации всегда следует разделять выборку, по крайней мере, на две группы и проводить их независимую кластеризацию, чтобы увидеть, образуются ли одинаковые кластеры в обеих группах.

Существует несколько методов группировки объектов в кластеры. При иерархической кластеризации чаще всего используют методы одиночной, полной, средней связи, метод Варда, центроидный метод.

Неиерархическая кластеризация отличается тем, что она позволяет объектам покидать один кластер и присоединяться к другому в процессе образования кластеров, если это улучшает показателя кластеризации. Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы:

(1) минимизировать изменчивость внутри кластеров;

(2) максимизировать изменчивость между кластерами.

Неиерахическая кластеризация более надежна, чем иерархическая. При неиерархической кластеризации всегда задается определенное количество кластеров, которые и будут выделены в процессе анализа. Исследователю приходится выбирать число кластеров априори, что может быть трудной задачей.

Этапы кластерного анализа. Кластерный анализ выполняется за несколько этапов. Для того чтобы активировать программу кластерного анализа, необходимо в меню «Statistics» выбрать группу методов «Multivariate Exploratory Techniques» и далее метод «Cluster Analysis» (рис. 6.2).

Рис. 6.2. Меню выбора методов статистического анализа

На первом этапе выбирают переменные для кластеризации. Трудность заключается в том, чтобы отделить, исходя из теоретических представлений, наиболее важные, ключевые переменные, характеризующие объекты с нужной исследователю стороны, от «случайных», вариативных. Использовать в кластерном анализе все переменные полностью – не лучший выбор.

На втором этапе выбирается метод кластеризации (рис.6.3), способ вычисления расстояния между объектами или кластерами, количество кластеров, параметры кластеризации.

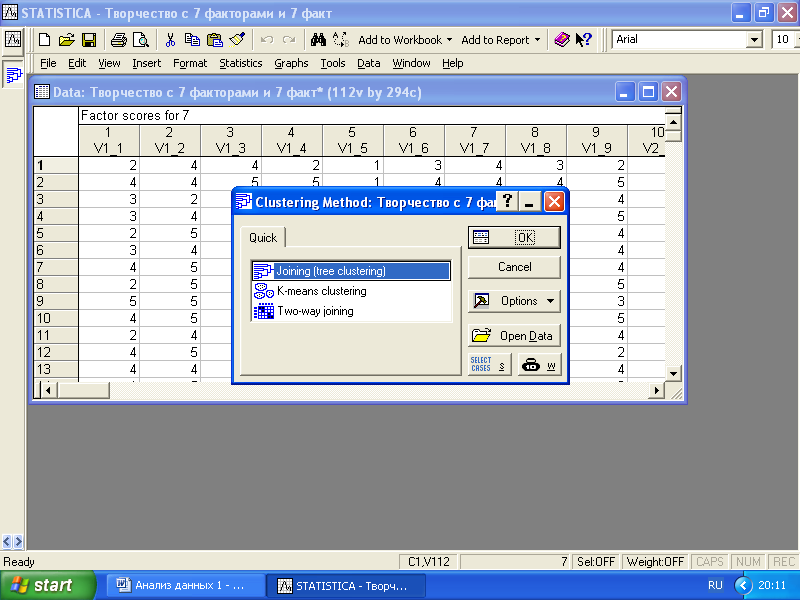
Рис. 6.3. Диалоговое окно выбора метода кластерного анализа

В появившемся диалоговом окне следует выбрать один из предложенных методов кластерного анализа: «Joining (tree clustering)» – иерархическая кластеризация, «K-means clustering» – неиерархическая кластеризация.

Выберем метод «K-means clustering», как более надежный. В результате будет открыто следующее окно (рис. 6.4).

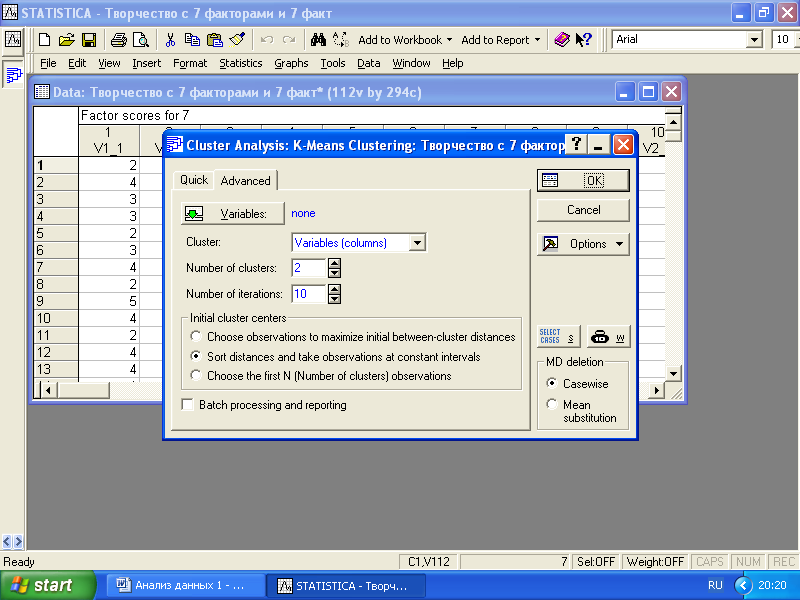
Рис. 6.4. Окно задания параметров кластерного анализа «K-means clustering»

В качестве переменных для кластеризации возьмем группу переменных V8_A1 – V8_A12 (развитость по самооценке студентов творческих способностей и компетентностей) и V8_B1 – V8_B12 (интерес студентов к развитию этих же способностей и компетентностей). Нажмем кнопку «Variables» и отметим эти переменные для анализа.

Следует установить параметр «Cases (rows)» в опции «Cluster», тогда объектами кластерного анализа будут отдельные случаи. Если оставить «Variables (columns), то объектами кластеризации станут не респонденты, а переменные и кластерный анализ сможет отчасти выполнить функцию факторного анализа.

Опция «Initial cluster centers» позволяет определить способ выбора определения кластерных центров до начала итераций. Для увеличения надежности кластерного анализа рекомендуется проверить несколько способов, что позволит оценить их влияние на результаты.

Далее необходимо определиться с количеством кластеров, которые будут выделены в процессе кластеризации. Какие-либо рекомендации здесь дать трудно. Желательно просмотреть все разумные варианты (от двух до семи кластеров), оценивая результат кластеризации как с теоретической точки зрения, так и с использованием статистических критериев.

Обычно, когда результаты кластерного анализа методом K средних (K-means clustering) получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.

Установим количество кластеров равным четырем в опции «Number of clusters», нажмем «ОК». В результате будет выведено окно результатов кластерного анализа (рис. 6.5).

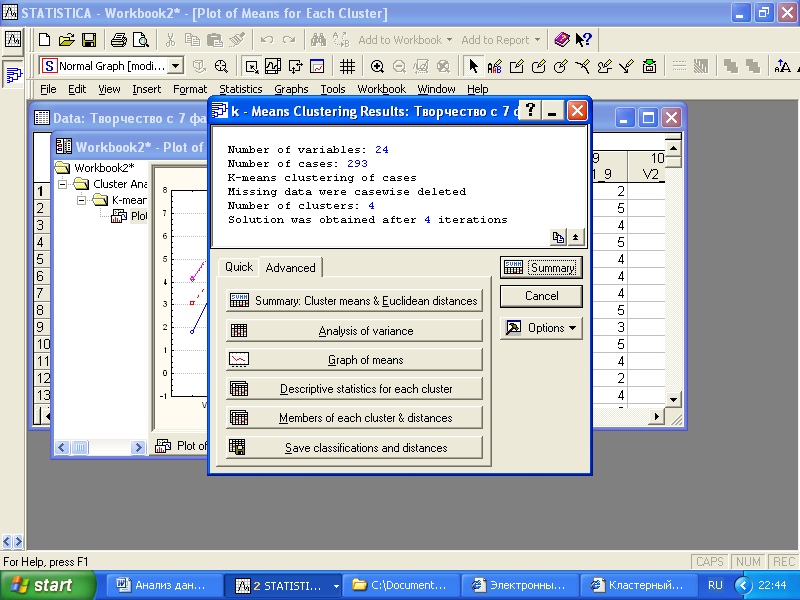
Рис. 6.5. Окно выводов результатов кластерного анализа «K-means clustering»

Быстро и удобно просматривать результаты кластеризации позволяет вывод графика средних значений для каждого кластера. Нажмем кнопку «Graph of meanes», чтобы получить следующие графики (рис. 6.6).

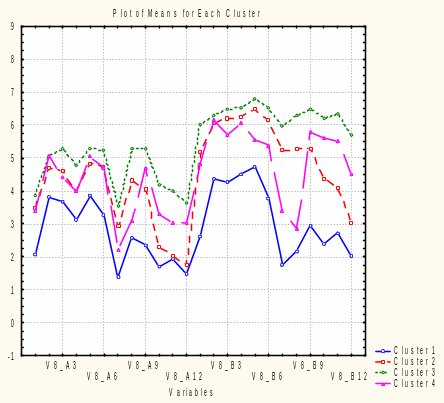
Рис. 6.6. Графики средних значений для каждого кластера

Визуальный анализ средних значений по каждой анализируемой переменной каждого кластера позволяет выявить следующую типологию.

Первый кластер – это студенты, оценившие себя как «малокомпетентные в творчестве», «с неразвитыми творческими способностями». Показательно, что и интерес к развитию творческих способностей и компетентностей среди этой группы студентов находится на самом низком уровне. Небольшой интерес прослеживается к развитию «чувства внутренней свободы», «умению импровизировать», «развитию интуиции».

Третий кластер - студенты с наиболее развитой творческой компетентностью (по самооценке), проявляют наибольший интерес (среди других кластеров) к дальнейшему развитию своих способностей и знаний в творчестве. Для этой группы студентов характерен интерес ко всем предложенным темам: от знания техник, закономерностей, концепций творчества до умения путешествовать в мирах воображения, входить в особые состояния сознания.

Второй и четвертый кластеры занимают промежуточные положения между первым и третьим кластерами, отличаясь, по всей видимости, общей установкой на воображение или рациональность.

Студенты, вошедшие во второй кластер, оценивают себя как «умеющие путешествовать в мирах воображения». Они, в сравнении со студентами четвертого кластера, лучше «умеют входить в особые состояния сознания», но не имеют знаний о техниках творчества, психологических закономерностях творчества, концепциях творчества. Представители четвертого кластера, наоборот, по сравнению со вторым, больше знают, но меньше «путешествуют и воображают». Соответственно студенты, составляющие второй кластер, проявляют высокий интерес ко всем предложенным темам за исключением увеличения знаний о творчестве. Студенты четвертого кластера не интересуются «умением входить в особые состояния сознания», «умением путешествовать в мирах воображения».

Общий вывод, который может быть сделан по результатам кластеризации: интерес студентов к развитию творческой компетентности взаимосвязан с их оценкой собственной компетентности. Чем выше уровень самооценки, тем выше уровень интереса.

Более точные сведения о средних значениях кластеров по каждой переменной можно получить, нажав кнопку «Descriptive Statistics for each cluster». В выводимых таблицах (рис. 6.7) указано и количество объектов в каждом кластере:

1-й кластер (малокомпетентные) – 46 студентов;

2-й кластер (умеренно компетентные «путешественники в мирах воображения») – 112 студентов;

3-й кластер – (высококомпетентные) – 84;

4-й кластер – (умеренно компетентные «рационалисты») – 51 студент.

Рис. 6.7. Описательная статистика для первого кластера

Нажатие кнопки «Analysis of variance» позволяет вывести результаты F-статистики для оценки приемлемости разделения респондентов на найденные кластеры (рис. 6.8). F-критерий показывает отношение межгрупповой дисперсии (суммы квадратов) к внутригрупповой дисперсии. Чем больше F-отношение, тем лучше результаты кластеризации по определенной переменной. Можно ориентироваться и на p-уровень значимости.

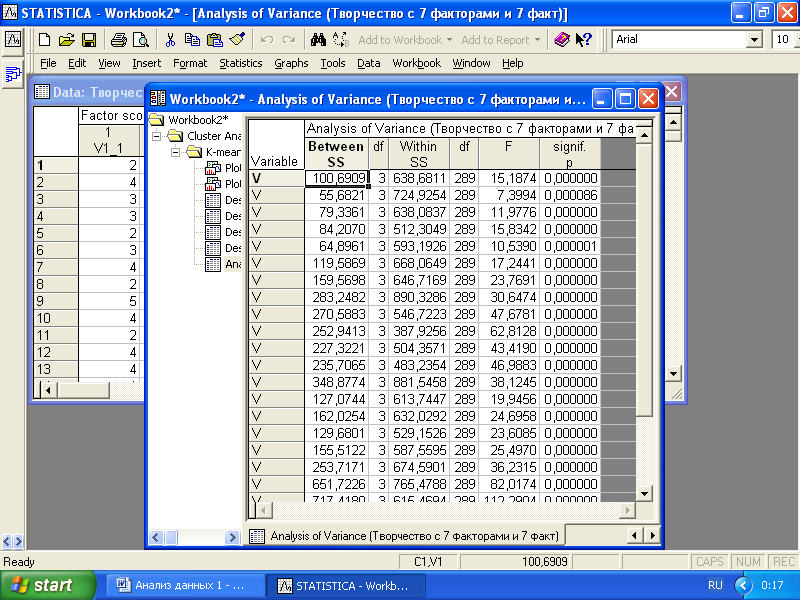
Рис. 6.8. Результаты F-статистики для оценки приемлемости разделения респондентов на найденные кластеры

Судя по результатам F-статистики, отделимость кластеров вполне приемлемая. Можно сравнить по этому критерию результаты кластеризации с использованием различного числа кластеров.

Нажатие кнопки «Cluster meances&Euclidean Distances between Clusters» позволяет вывести данные о средних значениях и евклидовом расстоянии между центрами найденных кластеров (рис. 6.9, 6. 10).

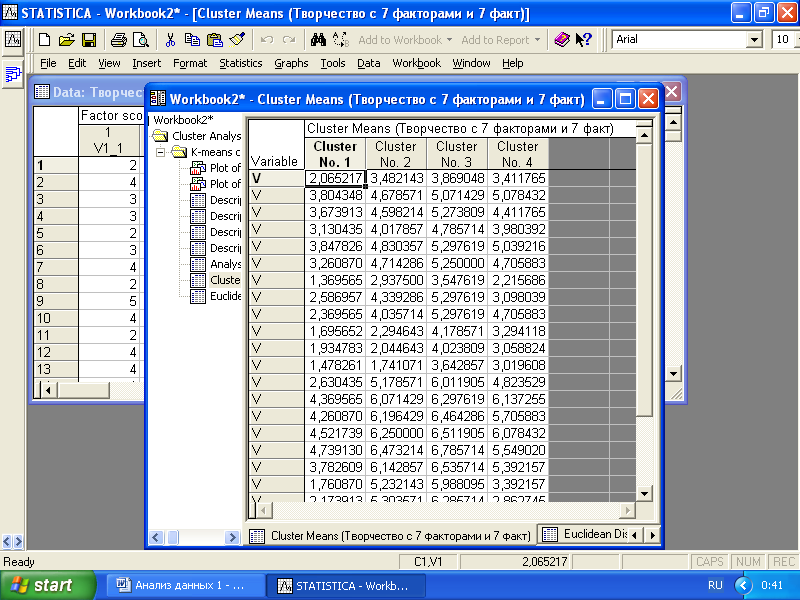
Рис. 6.9. Таблица средних значений для найденных кластеров

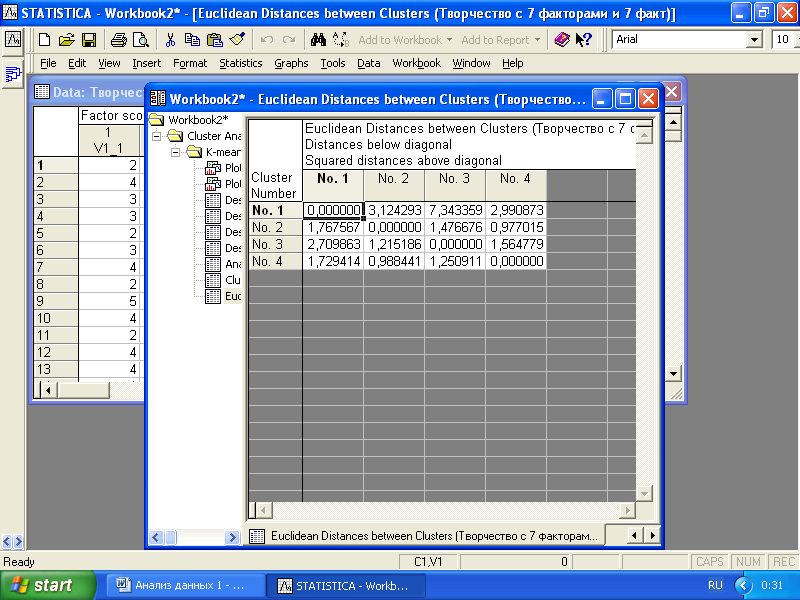
Рис. 6.10. Евклидово расстояние между центрами кластеров

Наконец, результаты кластеризации можно использовать для дальнейшего анализа, при этом в таблице данных будут образованы новые переменные: номер кластера (cluster), дистанция респондента от центра кластера (distance) (рис. 6.11).(ер кластера"ьтаты кластеризации можно использовать для дальнейшего анализа, при этом в таблице данных будут образованы новые п

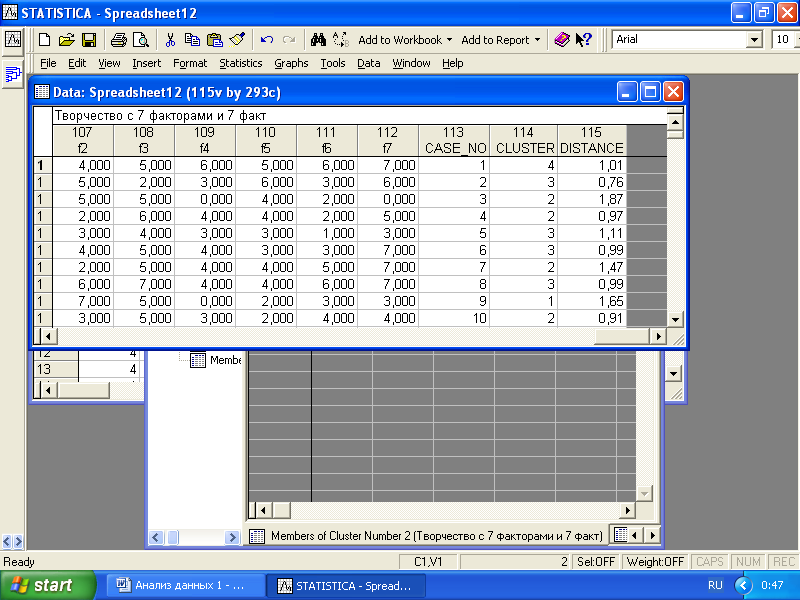
Рис. 6.11. Таблица данных с добавленными новыми переменными, отражающими результат кластеризации

Для того чтобы сохранить результаты кластеризации, следует нажать кнопку «Save classifications and distances». Сохранение результатов кластеризации в виде новой переменной (claster) позволяет выявить различие средних значений между кластерами по всем используемым в анализе переменным.

Проанализируем различие средних значений между кластерами по переменной V5 (вероятность прохождения студентами тренинга по современным технологиям творчества). Для этого можно использовать уже знакомый нам однофакторный дисперсионный анализ5вайте проанализируем различие средних между кластерами по переменной 544 4

0000000000000000000000000. В меню «Statistics» выберем «Basic Statistics/Tables» и метод «Breakdown & One-way ANOVA». В открывшемся окне зададим переменные для анализа: V5 – зависимая переменная, Cluster – группирующая (рис. 6. 12).

Рис. 6.12. Окно задания анализируемых переменных дисперсионного анализа

После того как задали переменные, нужно нажать «ОК». Затем в подменю «Quick» выведем результаты дисперсионного анализа, нажав кнопку «Analysis of Variance», и средние значения по кластерам, нажав кнопку «Summary» (рис. 6. 13).

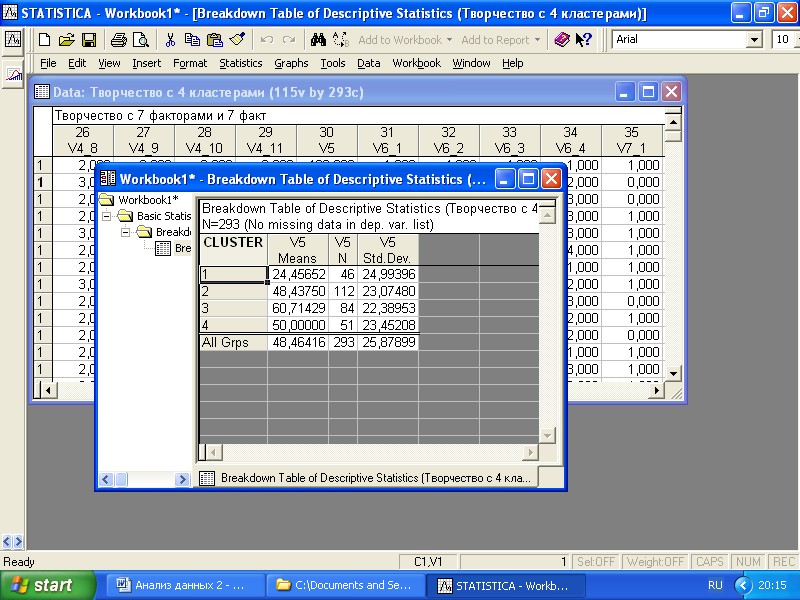
Рис.6.13. Таблица описательной статистики для кластеров

Дисперсионный анализ показал, что выбранные нами кластеры статистически значимо различаются по переменной V5 (желание пройти тренинг по технологиям творчества). Наибольшая вероятность того, что студент пройдет тренинг, определяется его принадлежностью к третьему кластеру (проявляющие наибольший интерес к творчеству). Наименьшая вероятность – принадлежность к первому кластеру. Довольно очевидный результат.

Скорее всего, количество выделенных нами кластеров не позволило получить более дифференцированные по интересам к развитию творческой компетентности группы студентов. Следовательно, необходимо попробовать увеличить количество рассматриваемых кластеров.

Задания:

1. Выделите семь кластеров по переменным, отражающим степень интереса к творческой компетентности и самооценку творческой компетентности. Дайте характеристику типичным представителям каждого кластера (по средним значениям). Проанализируйте различия между кластерами по желанию пройти тренинг.

2. Проанализируйте различия между кластерами по ассоциациям с творчеством, используя результаты проделанного нами факторного анализа.

Список рекомендуемой литературы

1. Методы сбора информации в социологических исследованиях. – Кн. 1-2. – М., 1990.

2. Боровиков, В.П. STATISTICA – Статистический анализ данных в среде Windows / В.П. Боровиков, И.П. Боровиков. – М., 1998.

3. Вуколов, Э.А. Основы статистического анализа: практикум по статистическим методам и исследованию операций с использованием пактов STATISTICA и EXCEL: учеб. Пособие / Э.А. Вуколов. – М., 2004.

4. Ядов, В.А. Социологическое исследование: методология, программа, методы / В.А. Ядов. – М., 1995.

5. Девятко, И.Ф. Методы социологического исследования / И.Ф. Девятко. – М., 2002.

6. Аакер, Д. Маркетинговые исследования. – 7-е изд. / Д. Аакер, В. Кумар, Дж. Дэй. – СПб., 2004.

7. Малхотра, Нэреш К. Маркетинговые исследования: практ. руководство. – 3-е издание / Нэреш К. Малхотра. – М., 2002.

Учебное издание