
- •Анализ данных в социологическом исследовании
- •Введение
- •1. Кодирование переменных. Подготовка данных к анализу
- •2. Описательная статистика (Descriptive statistics)
- •Сравнение средних значений. Однофакторный дисперсионный анализ
- •Факторный анализ
- •Кластерный анализ
- •Стариков Павел Анатольевич Анализ данных в социологических исследованиях
- •660041 Красноярск, пр. Свободный, 79
Сравнение средних значений. Однофакторный дисперсионный анализ
Сравнение средних значений – это мощное аналитическое средство выявления статистически достоверных закономерностей. Суть подхода заключается в том, чтобы сравнить два средних значения по определенной переменной для разных выборок на предмет достоверности их различия.
Так, например, мы получили следующие результаты анализа. Среднее значение переменной, отражающей ответы студентов на вопрос «Связан ли у Вас творческий процесс с негативными переживаниями», равно 2,94. Измеряя средние значения отдельно для выборки студентов и выборки студенток, мы получили значения 2,89 и 2,96. Имеем ли мы право на этом основании сделать вывод об отсутствии гендерного фактора в изучаемом вопросе (наличие негативных переживаний, связанных с творчеством)?
Сделать статистически достоверные выводы о различии позволяют специальные статистические методы. Прежде всего, необходимо определить, какой группой методов можно пользоваться. Выделяют методы параметрической (основанной на нормальном распределении) и непараметрической статистики. Давайте вначале рассмотрим группу методов параметрической статистики.
Параметрические методы. T-тест для независимых выборок. Наиболее часто в исследованиях используется t-критерий Стьюдента. Основное требование к данным для применения этого критерия – представление переменных, по которым сравниваются выборки, в метрической шкале измерения. Если есть сомнения в соответствии этому требованию, то следует воспользоваться непараметрическими методами. Достоинство T-теста состоит в том, что он может быть применен и по отношению к малым выборкам (меньше 100) в том случае, если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны.
Сравнение средних значений с помощью T-теста осуществляется следующим образом. Рассчитывается t-критерий, зависящий от объемов выборок, разброса данных. Затем найденное для данных значение t сравнивается с t критическим, которое определяется исходя из уровня заданной исследователем статистической достоверности (P). Обычно P принимается равным 0,05. Если t больше t критического, то делается вывод о статистически достоверном различии средних значений.
В пакетах статистических программ поступают несколько иным образом. Здесь рассчитывается t-критерий и критический уровень статистической значимости. По показателям этого уровня (обычно если он меньше 0,05) делается вывод о достоверности различий.
Давайте последовательно проделаем необходимые этапы сравнения средних для разных выборок. Войдите в меню «Statistics» и выберите «Basic Statistics/Tables». Появится следующее диалоговое меню (рис. 3.1).
Рис. 3.1. Диалоговое меню Basic Statistics/Tables
Выберите статистический метод анализа «T-test, independent, by groups» – сравнение средних значений с помощью T-теста для двух независимых выборок. В появившемся окне задайте переменные для анализа (рис. 3.2).
Рис. 3.2. Диалоговое окно задания переменных для метода «t-test, independent, by groups»
В этом методе вам необходимо отметить две переменные: зависимую (dependent) и группирующую (grouping). Группирующую переменную мы выбираем V12_1 – пол респондентов. В качестве зависимой переменной берется метрическая переменная, относительно которой сравниваются средние значения. Здесь мы устанавливаем в качестве группирующей переменную V9 – степень связи творческого процесса с негативными переживаниями. Теперь T-тест будет сравнивать средние значения переменной V9 для двух групп респондентов, образованных категориями группирующей переменной V12_1 - male и female. Нажмите «OK». Перед вами появится диалоговое меню (рис. 3.3).
Рис. 3.3. Диалоговое меню метода «T-test, independent, by groups»
Нажмите «Summary: T-tests». В результате будет выведена таблица с необходимыми статистическими результатами анализа (рис 3.4).
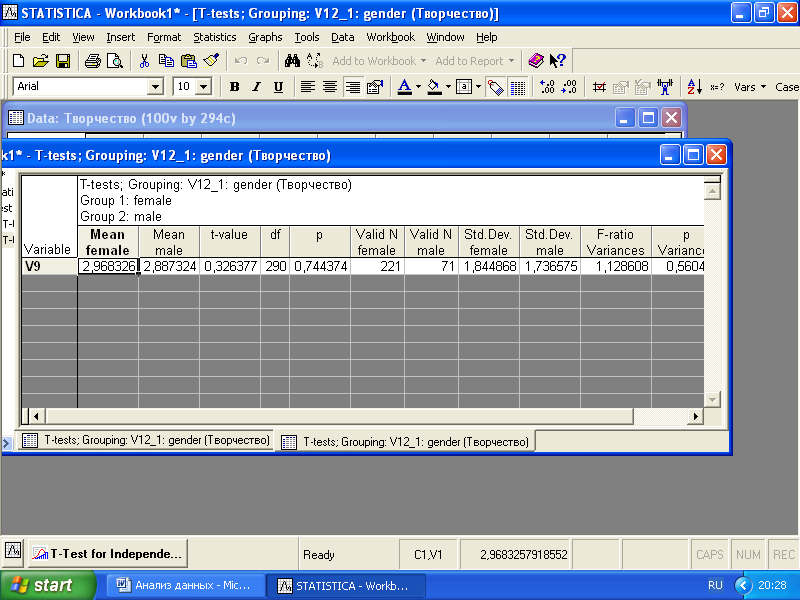
Рис. 3.4. Таблица с результатами T-теста
Наиболее значимые расчетные характеристики, на которые следует обратить внимание:
«Mean female» и «Mean male» – средние значения переменной V9 для женской и мужской выборок;
t-value – рассчитанное для данных выборок значение t-критерия;
df – число степеней свободы;
p-уровень статистической значимости t-критерия (значение p>0,05 указывает на то, что разность между средними значениями случайна);
p-уровень равен вероятности, при которой можно ошибочно отвергнуть гипотезу о равенстве средних двух выборок, когда в действительности эта гипотеза имеет место;
Valid N femail –- объем (количество респондентов) выборки женщин;
Valid N mail – объем выборки мужчин;
F-ratio Variances – F-критерий, который используется для проверки предположения о равенстве дисперсий между сравниваемыми выборками, что является условием применения Т-теста;
p Variances – если p < 0,05, то условия применимости t-критерия не выполнены и следует использовать непараметрические альтернативы t-критерия.
Применительно к конкретному анализируемому случаю можно сказать следующее. Исходя из того, что p Variances > 0,05, считаем Т-тест применимым в данном случае. Значимость p = 0,74 больше 0,05. Делаем вывод, что между студентами и студентками по изучаемому признаку нет статистически достоверных различий.
Теперь давайте выполним Т-тест сразу для списка зависимых переменных. Отметьте в диалоговом окне группу переменных V8_B1 – V8-B12 (интерес студентов к развитию определенных творческих способностей и компетентности). Группирующую переменную мы выбираем V12_1 – пол респондентов. Нажмите «Summary: T-tests». В результате будет выведена таблица с необходимыми статистическими результатами анализа (рис. 3.5).
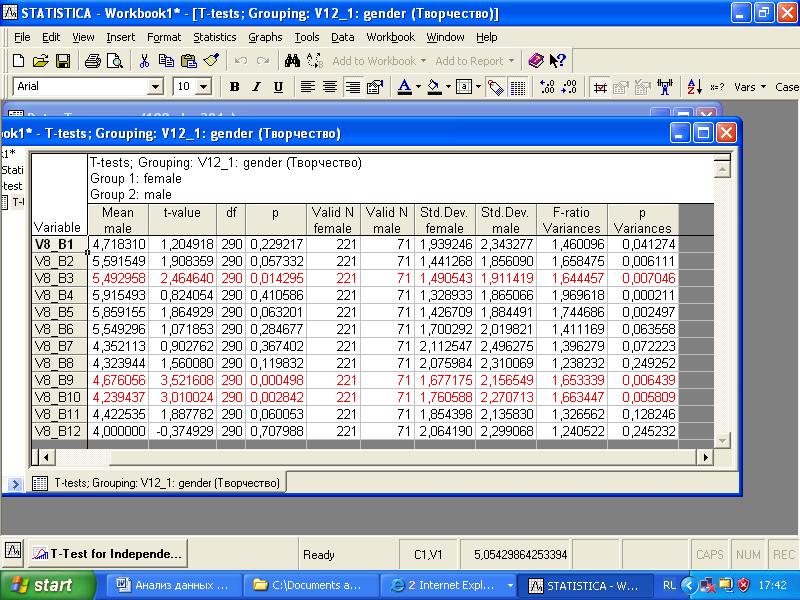
Рис. 3.5. Таблица результатов выполнения T-теста
В появившейся таблице результатов красным цветом выделены статистически достоверные различия по соответствующим переменным, что удобно при анализе большого количества переменных. Интерес студентов мужского и женского пола статистически достоверно различается к «умению импровизировать», «умению видеть уникальность мира, людей», «знанию техник творчества». Настроить параметры выделения красным цветом можно в «Options» посредством задания «p-level for highlightin».
Непараметрические методы. Эта группа методов специально создана для того, чтобы с помощью определенных статистических процедур обрабатывать данные "низкого качества" из выборок малого объема с переменными, про распределение которых мало что или вообще ничего не известно. Говоря более специальным языком, непараметрические методы не основываются на оценке параметров (таких как среднее или стандартное отклонение) при описании выборочного распределения интересующей величины. Поэтому данные методы иногда также называются свободными от параметров.
Непараметрическими альтернативами t-критерию для независимых выборок являются критерий серий Вальда–Вольфовица, U-критерий Манна–Уитни и двухвыборочный критерий Колмогорова–Смирнова.
Рассмотрим более подробно применение критерия Манна–Уитни, который позволяет установить различия между двумя независимыми выборками для зависимой порядковой переменной. Критерий Манна–Уитни используют и в тех случаях, когда можно использовать t-критерий. Однако он менее чувствителен к различиям (менее мощный), чем t-критерий.
Для анализа данных полученных с помощью нашей анкеты критерий Манна–Уитни будет правильно применить, например, к порядковым переменным: V6_1 – V6_4.
В меню «Statistics» выберите из списка методов «Nonparametrics», затем – «Comparing two independent samples» (рис. 3.6).
Рис. 3.6. Меню методов непараметрической статистики
В открывшемся диалоговом окне введите значения зависимой (V6_1 – V6_4) и группирующей (V12_1) переменных. Чтобы выполнить сравнение средних с помощью критерия Манна–Уитни, щелкните мышью по «Mann–Whitney U test». В результате будет выведена следующая таблица результатов (рис. 3.7).
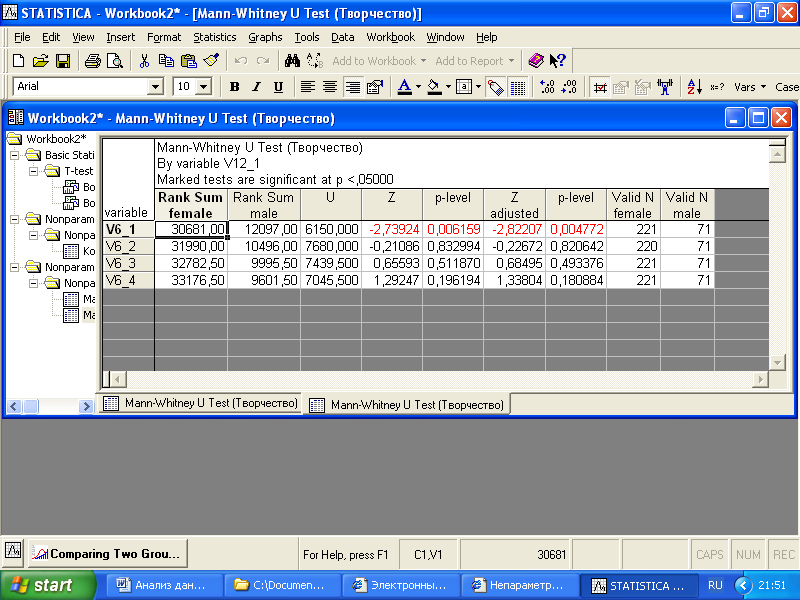
Рис. 3.7. Таблица результатов сравнения средних значений по критерию Манна–Уитни
Красным цветом в таблице выделена строка, относящаяся к переменной V6_1. Уровень статистической значимости (p-level) для этой переменной существенно меньше 0,05, что позволяет сделать вывод о наличии гендерных различий. Для остальных переменных гендерные различия не являются статистически достоверными.
Что делать, если группирующая переменная имеет количество категорий больше, чем два? В этом случае необходимо специально определить, какие категории переменной следует взять для формирования групп, между которыми будут производиться сравнения. Например, переменная V12_2 (курс, на котором обучается студент) имеет пять категорий. В поле «Codes for groups» следует вписать названия кодов тех категорий, которые будут взяты для сравнения (рис. 3.8).
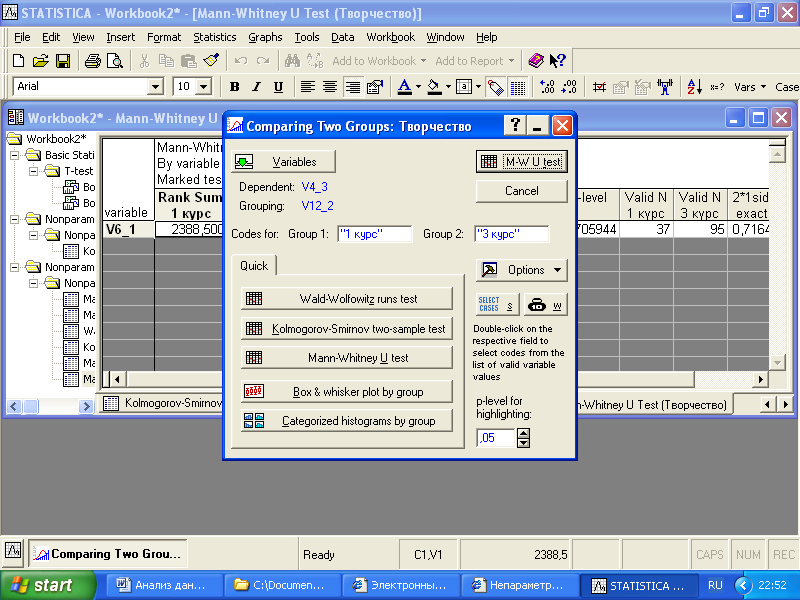
Рис. 3.8. Диалоговое окно «Comparing two independent samples»
Однофакторный дисперсионный анализ
Дисперсионный анализ – это процедура сравнения средних значений выборок, так же, как и t-критерий. В отличие от t-критерия дисперсионный анализ предназначен для сравнения не двух, а нескольких выборок. Например, применение метода дисперсионного анализа позволит ответить на вопрос: влияет ли курс (группирующая переменная – V12_2 имеет пять категорий) на творческие способности и компетентность студентов (метрические переменные V8_A1 – V8_A12)?
При однофакторном дисперсионном анализе сравниваются средние значения каждой выборки друг с другом и вычисляется общий уровень значимости различий. При этом данный метод анализа применяется в отношении метрической зависимой переменной, относительно которой рассчитываются средние значения, и единственной номинальной группирующей переменной.
Слово «дисперсионный» (ANOVA) в названии метода означает, что в процессе анализа сопоставляются компоненты дисперсии изучаемой переменной. Общая изменчивость переменной раскладывается на две составляющие: межгрупповую (факторную) дисперсию, обусловленную различием средних значений групп, и внутригрупповую (ошибки), обусловленную случайными, неучтенными причинами. Чем больше частное от деления межгрупповой и внутригрупповой дисперсии или изменчивости (F-отношение), тем больше различаются средние значения сравниваемых выборок и тем выше статистическая значимость этого различия.
Мы с вами рассмотрим самую простую модель дисперсионного анализа – однофакторную. Существуют также модели многомерного дисперсионного анализа как для множества зависимых переменных, так и для множества группирующих переменных (факторов).
Для того чтобы выполнить однофакторный дисперсионный анализ, необходимо в меню «Statistics» выбрать «Basic Statistics/Tables». В открывшемся диалоговом окне затем выбрать «Breakdown & One-way ANOVA» (рис. 3.9).
Рис. 3.9. Фрагмент меню Basic Statistics
Далее следует выбрать «Individual tables», задать группирующую переменную (фактор) и зависимую переменную. В качестве группирующей переменной возьмем V12_2 (курс респондентов), в качестве зависимой отметим сразу список переменных V8_A1 – V8_A12 (творческие способности и компетентность студентов). При этом дисперсионный анализ будет выполнен для каждой из зависимых переменных отдельно. В поле «Codes for grouping variables» можно выбрать для анализа определенные категории группирующей переменной. По умолчанию в анализе будут участвовать все категории. Нажмите «ОК» и вы получите следующее диалоговое окно результатов дисперсионного анализа (рис.3.10).
Рис. 3.10. Окно вывода результатов ANOVA
Чтобы вывести на экран результаты дисперсионного анализа, следует выбрать опцию «ANOVA & tests» и далее – «Analisis of Variance» (рис. 3.11).
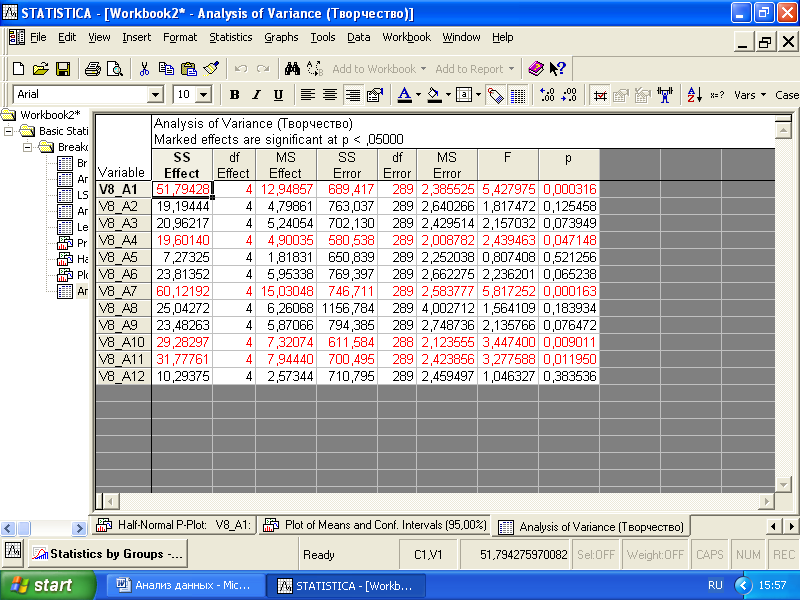
Рис. 3.11. Таблица результатов дисперсионного анализа
Красным цветом выделены переменные, относительно которых статистически достоверно установлено влияние фактора. В данном случае «курс обучения в вузе» влияет на такие творческие способности и компетентности, как «умение интегрировать сознание и бессознательные процессы», «умение генерировать оригинальные идеи», «умение входить в особые состояния сознания», «знание техник творчества», «знание психологических закономерностей творчества».
Нажатие «Interaction plots» позволяет визуализировать различия средних значений по отдельным группам (рис. 3.12). При этом имеет смысл выделить для анализа только те переменные, по которым установлено влияние фактора (V8_A1, V8_A4, V8_A7, V8_A10, V8_A11).
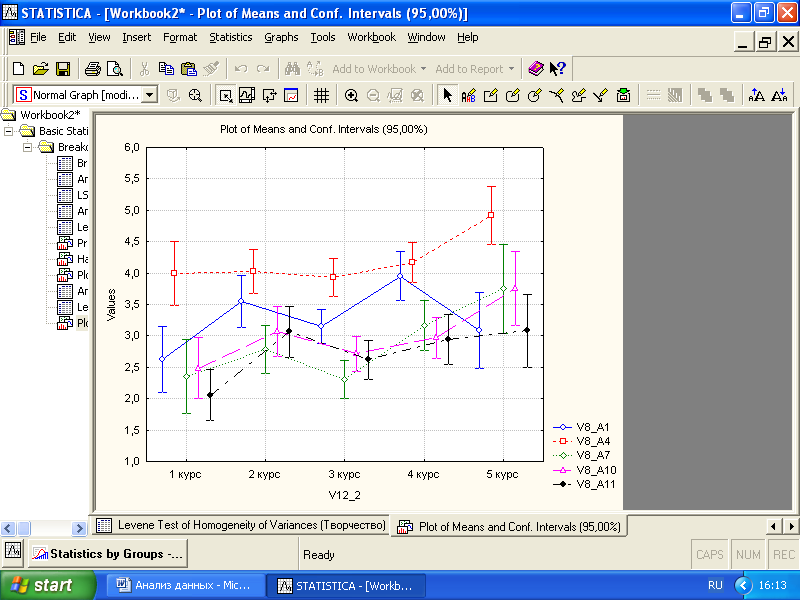
Рис. 3.12. График средних значений и доверительных интервалов
В целом графики отражают закономерный рост способностей и компетентности к творчеству в процессе обучения в университете. Обратите внимание на небольшой «провал» средних значений на уровне третьего курса по всем переменным. Возможно, причина заключается в так называемом «кризисе третьего курса», когда происходит переоценка своих знаний и возможностей в контексте лучшего понимания профессиональных задач. Необходимы дополнительные исследования, которые смогут подтвердить или опровергнуть это предположение.
Опция «Levene tests» позволяет выяснить с помощью критерия Левина корректность применения дисперсионного анализа (рис. 3.13).
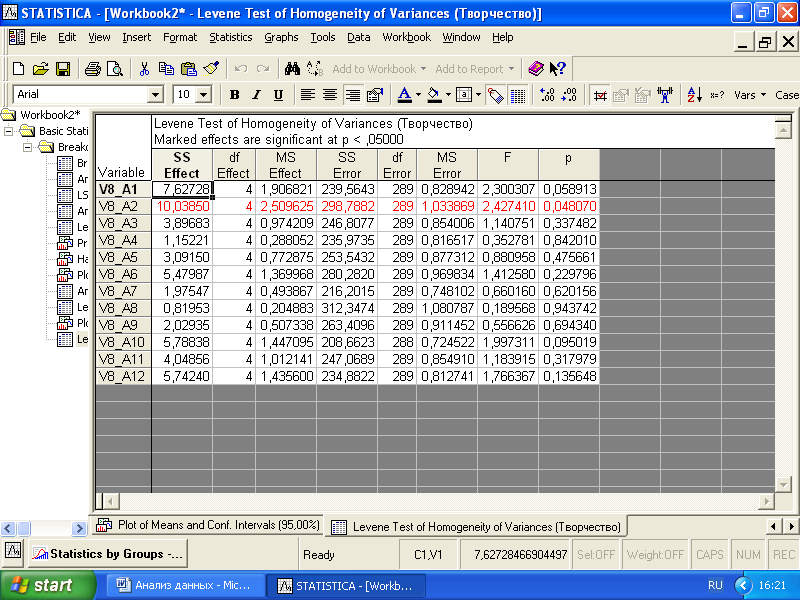
Рис. 3.13. Таблица результатов применения теста Левина
Критерий однородности дисперсии Левина во всех случаях (кроме одного) показал, что дисперсии для каждой из групп практически не различаются (p>0,05). Следовательно, результаты дисперсионного анализа, кроме переменной V8_A2, могут быть признаны корректными. Для переменной V8_A2 придется применить непараметрический аналог однофакторного дисперсионного анализа.
В опции «Post-hoc» исследователь получит возможность проанализировать все возможные сочетания групп на различие средних значений. Процедуры «Post-hoc» нужно выполнять, после того как с помощью дисперсионного анализа будет установлено статистически достоверное влияние фактора на изучаемую метрическую переменную.
Одним из наиболее консервативных (строгих) критериев для выявления различий средних значений будет критерий Шеффе. Красным цветом выделены пары, для которых различия средних значений статистически значимы (рис. 3.14). Так, значимыми оказались различия между студентами четвертого и третьего курсов, четвертого и первого курсов для переменной «умение интегрировать сознание и бессознательные процессы» (V8_1).
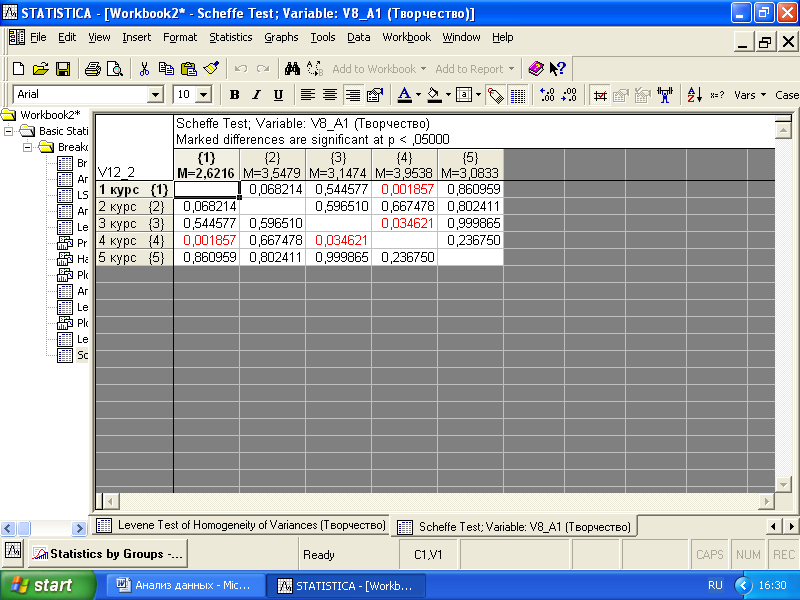
Рис. 3.14. Таблица результатов применения критерия Шеффе для сравнения средних значений между группами
Непараметрический аналог однофакторного дисперсионного анализа
Для сравнения более двух переменных по уровню выраженности переменной чаще всего применяется Н-критерий Краскала–Уоллеса. Этот критерий (в отличие от дисперсионного анализа) основан не на сравнении средних значений и дисперсий переменных, а на сравнении средних рангов.
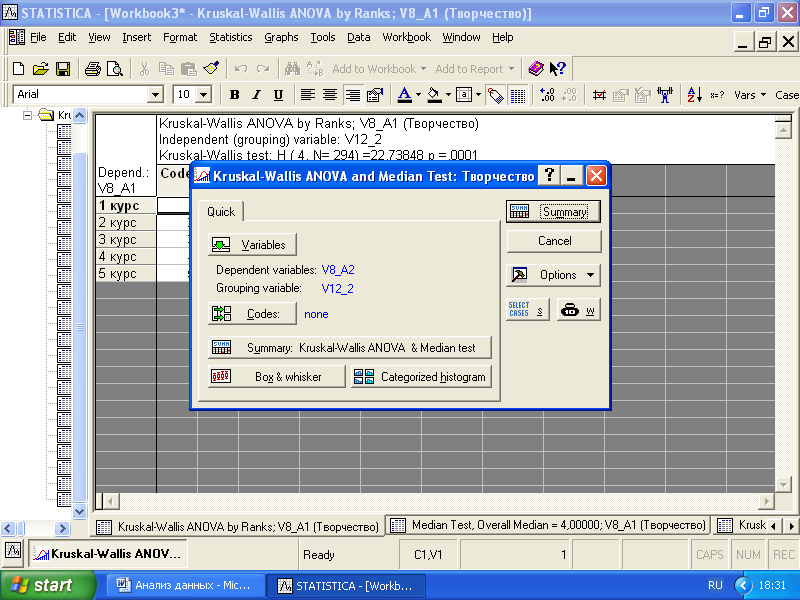
Рис. 3.15. Диалоговое окно для применения критериев Краскала–Уоллеса и медианного
В меню «Statistics» выберите из списка методов «Nonparametrics», затем – «Comparing multiple indep. samples». В открывшемся диалоговом окне задайте переменные для анализа: зависимая переменная – V8_A2; группирующая переменная – V12_2 (рис. 3.15).
Затем щелкните по «Summary», в таблице вывода результатов анализе наиболее важный результат – p-уровень статистической значимости (рис. 3.16).
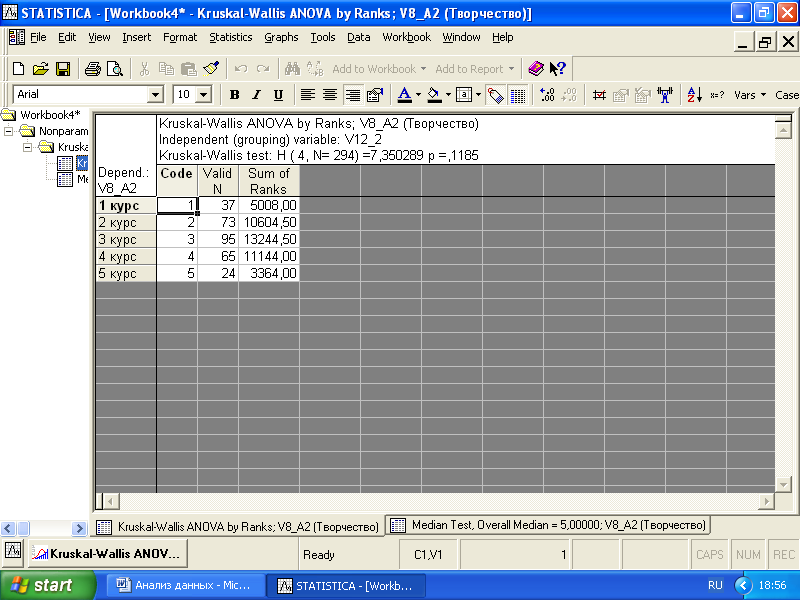
Рис. 3.16. Таблица результатов применения критерия Краскалла–Уоллеса
Значение p=0,12, следовательно, различия между группами не являются статистически достоверными. Схожие результаты, свидетельствующие о недостоверности различия между группами по переменной V8_A2, дает и критерий медиан (p=0,36).
Задание: Проанализируйте различия в интересе студентов к развитию определенных творческих способностей и компетентностей для различных курсов, факультетов. Найдите закономерности. Постройте объяснительные модели.
Таблицы сопряженности. Корреляционный анализ
Таблицы сопряженности, или кросстабуляции, служат для описания связи двух категориальных переменных. Например, нас может интересовать вопрос о взаимосвязи двух переменных: знакомство студентов с системой творчества ТРИЗ (переменная V2_3) и мнение о том, что от тренингов творчества нет никакой пользы (V6_1).
Для изучения взаимосвязи этих переменных можно расположить данные в виде таблицы сопряженности (рис. 4.1).
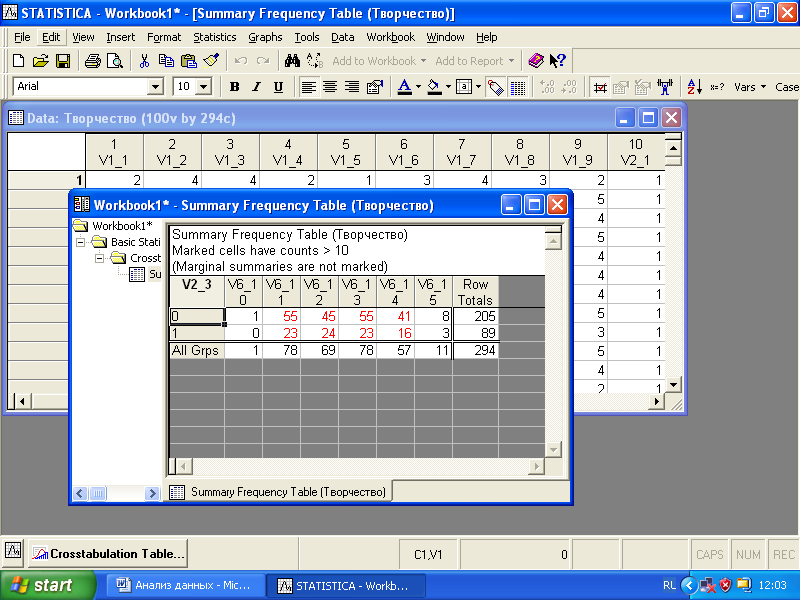
Рис. 4.1. Таблица сопряженности
Строки таблицы сопряженности соответствуют категориям переменой (V2_3), столбцы – категориям переменной (V6_1). В ячейках таблицы указаны частоты (количество респондентов, выбравших при ответах определенную категорию переменной V6_1 (столбец) и определенную категорию переменной V2_3 (строки)). В таблице частот обычно указываются маргиналы (сумма частот по строкам и столбцам).
Чтобы вывести на экран таблицу сопряженности, следует в меню «Basic Statistics» выбрать из списка «Tables and banners», а затем опцию «Crosstabulation» (рис. 4.2).
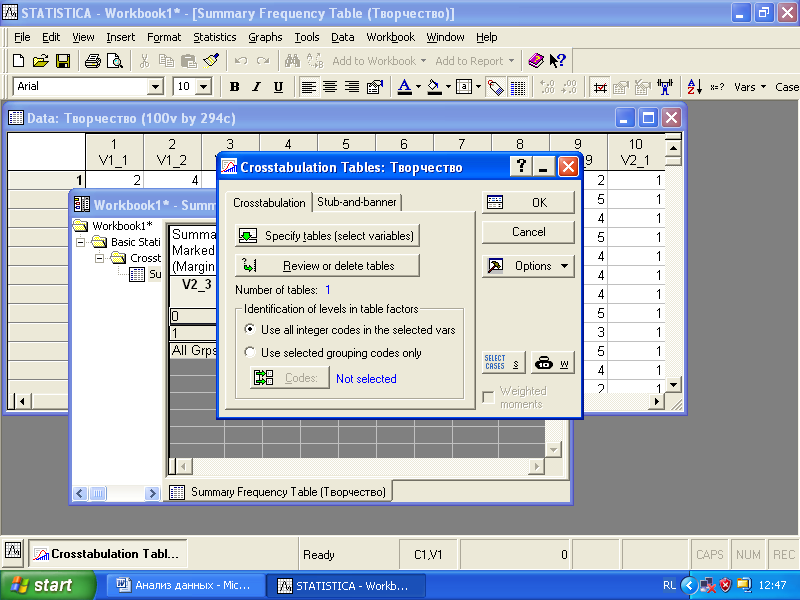
Рис. 4.2. Диалоговое окно задания таблиц сопряженности (кросстабуляции)
После этого нужно задать переменные таблицы сопряженности, открыв «Specify tables». Обычно создаются таблицы сопряженности двух переменных. Анализ таблиц сопряженности размерностью больше трех представляет значительные трудности, хотя можно задать и до пяти переменных. Отметим в первом листе для группирующих переменных V2_3, во втором – V4_1. Нажмем «ОК», и появится окно вывода результатов кросстабуляции (рис. 4.3). Для вывода на экран самой таблицы сопряженности следует нажать кнопку «Summary».
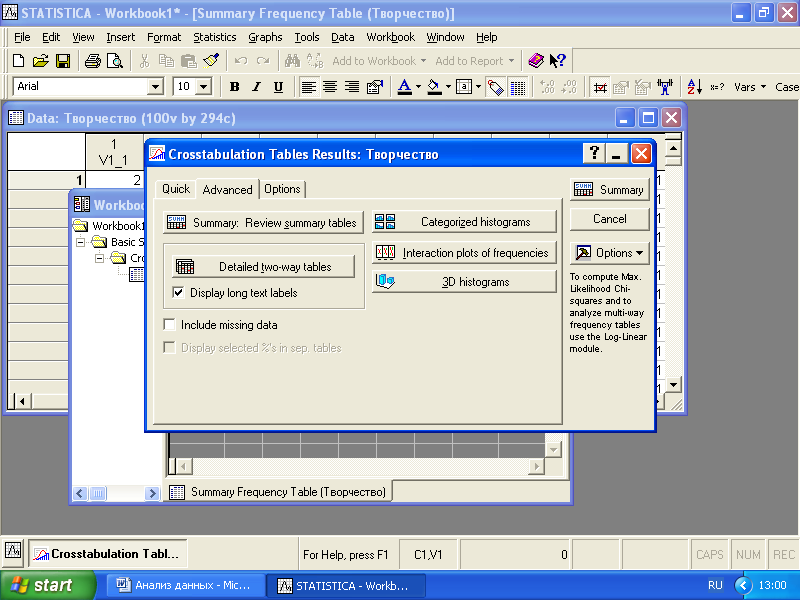
Рис. 4.3. Окно вывода результатов кросстабуляции
Еще один способ наглядного представления распределения частот при взаимодействии двух переменных (рис. 4.1) – использовать опции «3D histograms», «Categorized histograms» или «Interaction plots of frequencies».

Рис. 4.4. Графическое представление таблицы частот
В нашем случае одним визуальным наблюдением невозможно установить, есть ли между анализируемыми переменными статистически достоверная взаимосвязь. Одним из наиболее универсальных методов проверки наличия взаимовлияния переменных или их полной независимости друг от друга является использование критерия хи-квадрат.
Методика расчета критерия хи-квадрат очень простая. Сравниваются между собой две таблицы: с реальным распределением частот и таким теоретически-расчетным распределением частот, которое свидетельствовало бы о независимости переменных. Чем больше разница между реальным распределением и теоретически-расчетным, тем больше критерий хи-квадрат. Когда значение хи-квадрат становится больше критического, то принимается решение о зависимости переменных друг от друга.
Зачастую критерий хи-квадрат ошибочно воспринимается исследователями как сила связи между переменными. Однако это не так, критерий хи-квадрат используется только для доказательства зависимости или независимости переменных друг от друга. В то же время на основе критерия хи-квадрат конструируются различные коэффициенты сопряженности, которые служат мерой связи (коэффициент Фи, коэффициент Крамера). Эти коэффициенты принимают значение от 0 (полное отсутствие связи) до 1 (полная связь).
Чтобы получить информацию о степени связи между переменными, следует в «Options» отметить статистические критерии, коэффициенты сопряженности или корреляции, которые следует использовать (рис. 4.4).
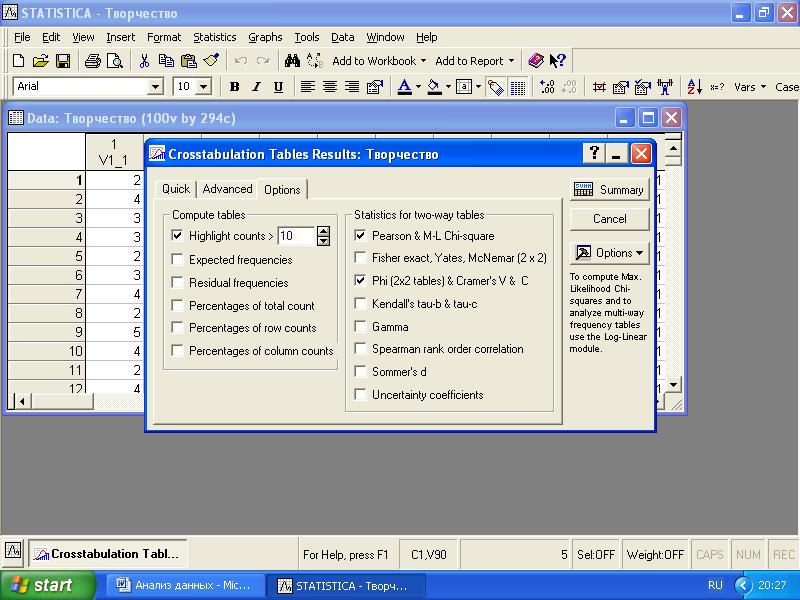
Рис. 4.5. Диалоговое окно задания статистик кросстабуляции
Далее в «Advanced» следует нажать кнопку «Detailed two-way tables» и считать необходимую статистическую информацию. В нашем случае связь между исследуемыми переменными отсутствует, поскольку уровень статистической значимости для критерия хи-квадрат имеет значение p=0,83 (то есть вероятность того, что связь отсутствует, равна 0,83). Соответственно коэффициенты сопряженности, производные от критерия хи-квадрат Фи, Крамера, контингенции, практически не отличаются от нуля.
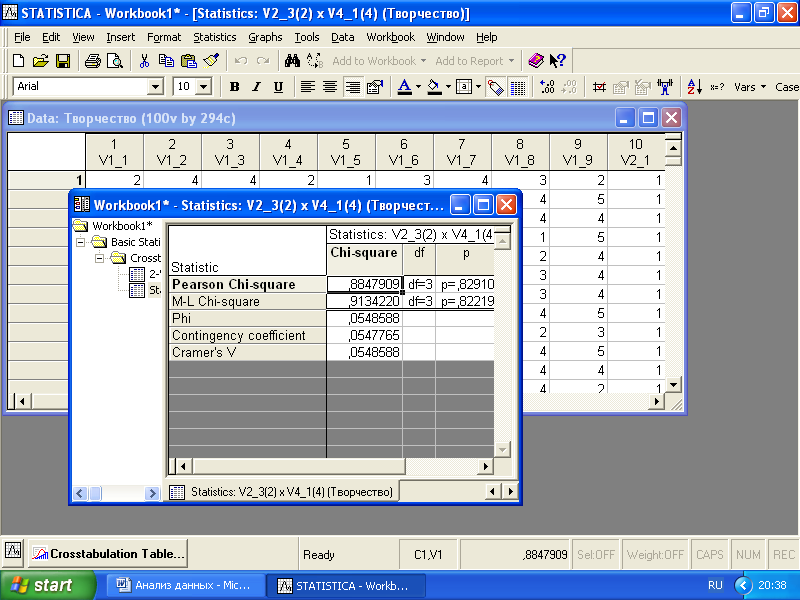
Рис. 4.6. Статистики связи двух переменных, основанные на критерии хи-квадрат
О чем может свидетельствовать установленное нами отсутствие связи между знанием студентами техник ТРИЗ и мнения о том, что от тренингов творчества нет никакой пользы? Видимо, о том, что эта система творчества в целом не считается студентами чудодейственной, решающей их актуальные проблемы. Использование аналогичных процедур для группы переменных V2_1 – V2_8 (знакомство с разнообразными техниками творчества) и переменной V4_1 (изначальное негативное отношение к тренингам творчества) показало следующее. Значимая связь существует только в отношении одной пары переменных – V4_1 и V2_8 (вхождение в особые состояния сознания). Коэффициент Крамера в этом случае равен 0,19. Научиться использовать особые состояния сознания для части студентов – это источник необходимых им изменений, ресурс, который вполне можно освоить в ходе тренинга.
Связь между переменными, измеряемыми по номинальной, порядковой, интервальной шкалл.
Существует множество мер связи. Каждая из этих мер годится для анализа только определенного типа данных, полученных с помощью соответствующих шкал (номинальной, порядковой, интервальной). Поэтому исследователь должен выбирать меры, наиболее пригодные для оценки связи между конкретными переменными. К ситуации «смешанных переменных» (к примеру, одна номинальная и одна порядковая) обычно применяется консервативный подход, т.е. выбор тех мер связи, которые подходят для более грубой из двух шкал измерения.
Для номинальных переменных используются две группы статистик, позволяющие рассчитать меры связи. Выше мы уже рассматривали применение статистик, основанных на критерии хи-квадрат, в пакете Statistica – коэффициент фи, V Крамера. Другой мерой служат вероятностные методы уменьшения ошибки (Uncertainty coefficient, lamda).
Для порядковых переменных существуют специально разработанные статистические методы расчета корреляций: Gamma (гамма), Spearman rank order correlations (коэффициент ро Спирмена), Kendall`s tau-b & tau-c (коэффициент ранговой корреляции тау Кендалла). Коэффициенты корреляций меняются в диапазоне от -1 до 1. Если коэффициент корреляции равен 0, то это свидетельствует об отсутствии какой-либо связи между исследуемыми переменными. Если коэффициент корреляции равен -1, то говорят о сильной отрицательной корреляции, если коэффициент корреляции равен 1, то о положительной. Смысл отрицательной корреляции можно понять из следующего примера: чем больше студент согласен с суждением «каждый человек либо талантлив, либо нет», тем меньше он склонен ассоциировать творчество с экстатическими переживаниями (коэффициент корреляции по Спирмену равен -0,2).
Взаимосвязи между порядковыми переменными удобно анализировать в меню непараметрической статистики (рис. 4.7).
В меню «Statistics» выберите из списка методов «Nonparametrics», затем – «Correlation ( …)».
Рис. 4.7. Меню методов непараметрической статистики
При этом открывается диалоговое окно (рис. 4.8). Далее задаются выделением два списка переменных: List 1 и List 2 в опции «Variables». На рис. 4.8 для анализа выбраны переменные V1_1 – V1_9 (согласие с суждениями о творчестве) и переменная V5 (согласие на участие в тренинге по творчеству).
Рис.4.8. Диалоговое окно непараметрических методов корреляции
Чтобы вычислить корреляционные связи между заданными переменными, следует нажать кнопки одного из трех методов: Gamma, Spearman rank R, Kendall tau. На рис. 4.9 дана корреляционная матрица, рассчитанная с использованием Spearman rank R, Gamma соответственно.
Красным цветом в таблицах выделены коэффициенты корреляции статистически достоверно отличные от нуля (по умолчанию уровень достоверности установлен 0,05). Отчетливо видно, что между парами переменной V5 и переменными V1_2, V1_3, V1_6, V1_7, V1_9 существует слабая корреляционная связь. Результаты использования различных методов Gamma, Spearman rank R практически не различаются. Нужно помнить, что при проведении корреляционного анализа оценка выраженности силы связи между переменными носит хоть и количественный, но достаточно условный характер.
О чем свидетельствуют выявленные нами корреляции? Во-первых, представления студентов о творчестве слабо, но влияют на желание студентов пройти соответствующий тренинг. Наиболее сильно с желанием пройти тренинг связаны представления, что «существуют эффективные методики развития творческого потенциала личности», «способность к творчеству помогает добиться успехов в жизни», «творчество – это источник подлинного удовольствия», «на современном рынке труда востребованы творческие люди» (коэффициенты корреляции составляют 0,16, 0,2, 0,18, 0,18 соответственно).
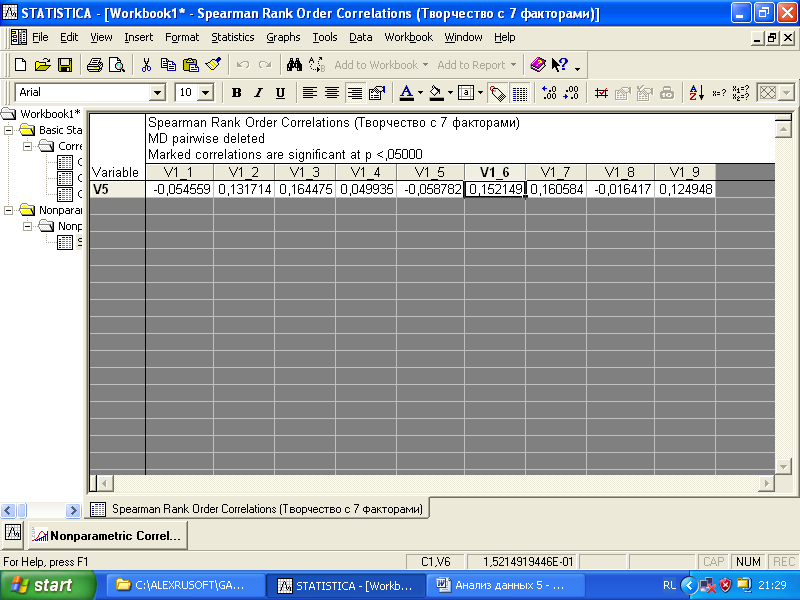
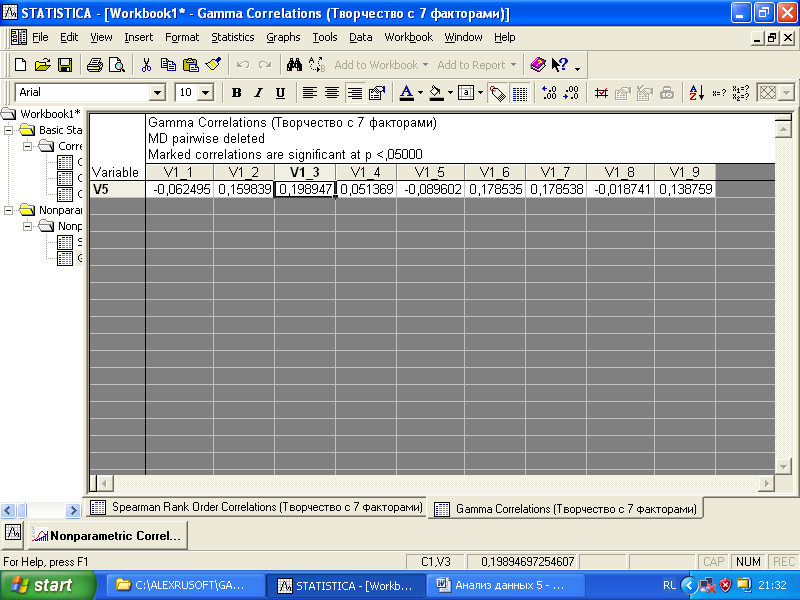
Рис. 4.9. Таблицы результатов корреляционного анализа
Для интервальных переменных широко применяется статистика, называемая коэффициентом корреляции r Пирсона. Подобно порядковым мерам связи, r Пирсона изменяется в диапазоне от -1 до +1, где 0 указывает на отсутствие связи, а +1 и -1 – на абсолютную положительную или отрицательную связь соответственно. Чтобы провести корреляционный анализ по Пирсону, необходимо выбрать в меню «Basic Statistics» подменю «Correlations». В открывшемся окне следует задать переменные для анализа. Можно использовать квадратные («One variable list») или прямоугольные («Two lists») корреляционные матрицы. Последние более удобны для того, чтобы определить, как влияют все переменные на небольшую избранную группу переменных. Когда переменных выбрано много, лучше установить «Pairwize» (если пропущено какое-нибудь значение, то из анализа будет убираться только пара данных, а не вся строка таблицы данных).
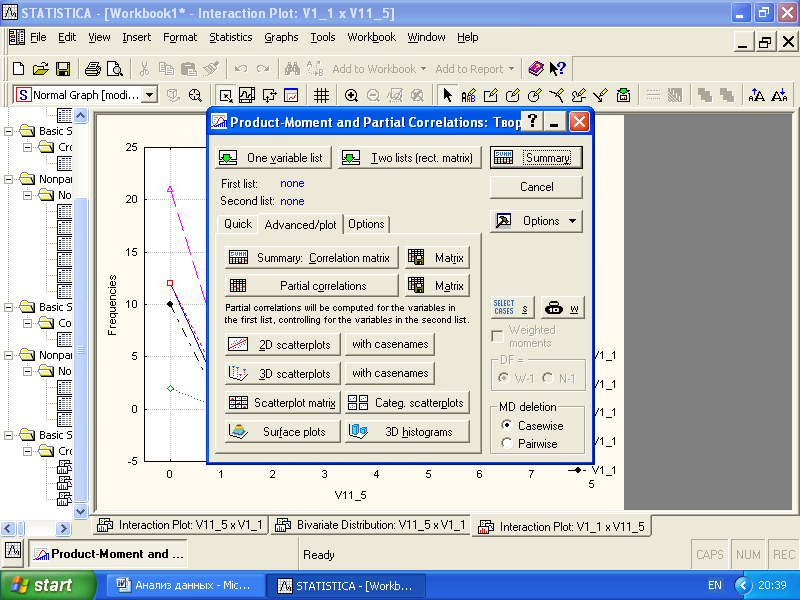
Рис. 4.10. Диалоговое окно корреляционного анализа по Пирсону
Нажатие кнопки «Summary» позволяет вывести на экран корреляционную матрицу (рис. 4.14). В качестве графических средств анализа следует отметить диаграммы рассеяния (Scatterplots). В наших данных отсутствуют переменные, для вывода которых было бы целесообразно использовать диаграммы рассеяния, поэтому для иллюстрации на рис. 4.11 приведен пример диаграммы рассеяния из другого исследования (по оси Х указан вес респондентов, по оси У – рост респондентов). Каждая отмеченная точка на диаграмме рассеяния соответствует одному случаю (респонденту). Видно, что точки в большей степени группируются вдоль кривой, выделенной красным цветом. Скопление точек по форме напоминает эллипс, при этом коэффициент корреляции между переменными отрицательный и равен -0,2.

Рис. 4.11. Диаграмма рассеяния
Для категориальных переменных, наряду с таблицами сопряженности, можно использовать объемные рисунки распределения частот. Нажав кнопку «3D Histograms», мы получим набор столбиковых диаграмм, позволяющий наглядно оценить взаимосвязь между переменными. На рис. 4.12 представлено сопряжение переменных, отражающих ассоциирование творчества с «целостным взглядом на мир» и с «импровизацией, спонтанностью». Коэффициент корреляции по Пирсону равен 0,36, что свидетельствует об умеренной положительной взаимосвязи между исследуемыми переменными.

Рис. 4.12. Объемная диаграмма сопряжения переменных V11_10 и V11_11
При интерпретации взаимосвязей группы переменных необходимо учитывать, что внутренняя логика взаимосвязей может быть очень сложной, нелинейной, опосредованной скрытыми латентными факторами. Как писал видный отечественный синергетик В.Г. Буданов, массу корреляционных зависимостей можно объяснить следующим образом. «Если мы имеем крону дерева, которое затоплено, и мы пошевелили ствол под водой, то все веточки начинают синхронно двигаться. Казалось бы, несвязанные явления, но наше сознание привыкло с детства искать конкретную причину. И мы начинаем искать взаимосвязи непосредственно между этими веточками, какая из них первая, кто из них на кого влияет. А причина в том, что где-то там колеблется общий ствол»2.
В целом корреляционный анализ служит мощным средством создания моделей изучаемого явления, понимания внутренней логики процессов. При этом используются специальные общие подходы к анализу взаимосвязей между переменными.
Во-первых, корреляционные связи изучаются системно, прослеживаются «узоры» всех статистически достоверных связей. Часто для этих целей используется построение максимального корреляционного графа. Вершины максимального корреляционного графа представляют собой отдельные переменные, их соединяют линии, отражающие статистически достоверные корреляции. При этом исследователь сам решает, какие связи должны быть обязательно отражены в максимальном корреляционном графе: наиболее сильные или те, которые важны для хорошего теоретического понимания сопоставляемых процессов. Для построения корреляционного графа обычно используется корреляционная матрица, для получения которой следует определить переменные и нажать кнопку «Summary: Correlation matrix». Предварительно в «Options» можно установить уровень p, чтобы окрашивать в корреляционной матрице более или менее значимые коэффициенты.
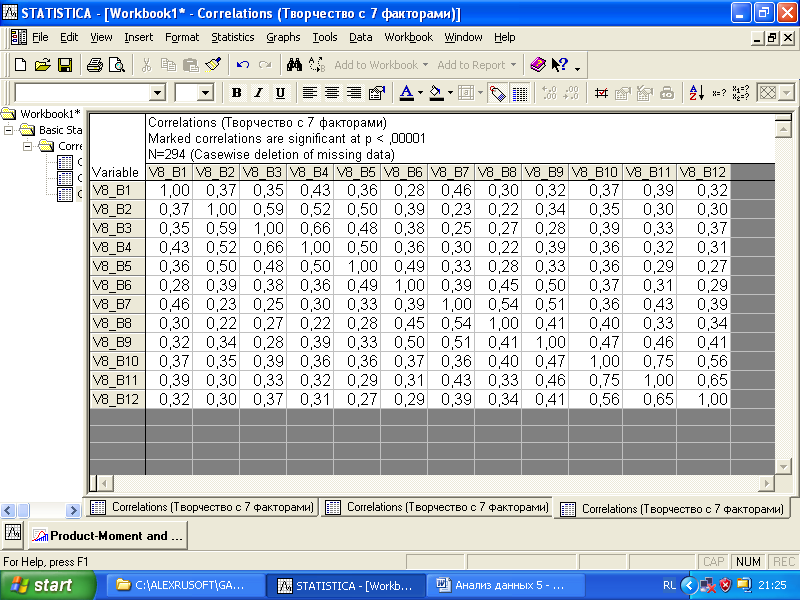
Рис. 4.13. Фрагмент корреляционной матрицы
В целом коэффициенты корреляции между переменными V8_B1 – V8_B12 показывают наличие статистически достоверных связей между всеми анализируемыми переменными. Интерпретировать эти результаты корреляционного анализа довольно просто. В целом найденные корреляции отражают следующую закономерность: если студенты проявляют интерес к творчеству, то они проявляют интерес и ко всем отдельным составляющим творческой компетентности. Однако можно выделить и «островки» наиболее тесно связанных интересов. Например, тесно взаимосвязана между собой группа переменных, отражающих интерес студентов к следующим темам: «чувство внутренней свободы», «умение импровизировать», «умение генерировать оригинальные идеи», «развитие интуиции» (переменные V8_B2, V8_B3, V8_B4, V8_B5 соответственно). Найденные взаимосвязи могут помочь проникнуть во внутренние бессознательные представления и ожидания студентов и понять, почему оказались связаны между собой проблемы интуиции, внутренней свободы, генерации оригинальных идей.
Другая тесно связанная группа – «знание техник творчества», «знание психологических закономерностей творчества», «знание философских, религиозных концепций творчества» (переменные V8_B9, V8_B10, V8_B11 соответственно). Здесь интерпретация взаимосвязей может быть более легкой – студенты проявляют комплексный интерес к знанию о творчестве. Можно выделить еще одну группу интересов студентов – «умение входить в особые состояния сознания», «умение путешествовать в мирах воображения». Сильная положительная корреляция между этими переменными (коэффициент корреляции составляет 0,55) свидетельствует о том, что проблематика воображения и измененных состояний сознания в представлении студентов находится «очень близко» друг от друга.
Максимальный корреляционный граф и строится для того, чтобы наглядно изобразить графически сложное переплетение взаимосвязей между переменными.
Во-вторых, при анализе корреляционных связей можно использовать метод уточнений – анализ взаимосвязей с введением дополнительных контрольных переменных. Метод уточнений в социологии был детально разработан в 1940–1950-е гг. П. Лазарсфельдом, С. Стауффером и их сотрудниками для анализа элементарных таблиц сопряженности и взаимосвязей номинальных переменных. Однако общая логика этого подхода используется и при изучении интервальных переменных посредством расчета частных корреляций.
Расчет коэффициента частной корреляции – это простейшее средство уточнения исходной модели при введении дополнительной переменной. Частной корреляцией называют корреляцию между двумя переменными, когда статистически контролируется или поддерживается на постоянном уровне третья переменная.
Например, В.А. Ядов в одной из своих книг по методологии социологических исследований рассказывал о случае ложного открытия, которое он сделал, будучи молодым ученым3. В то время Ядов исследовал проблему влияния уровня образованности на производительность труда рабочих. Была выявлена статистически значимая отрицательная взаимосвязь этих переменных: чем образованнее рабочий, тем хуже его производительность труда. На основании этих данных была разработана теория, опубликована монография. Позже Ядов признавался в совершенной ошибке. На самом деле отрицательную корреляционную взаимосвязь создала третья переменная – стаж работы. Образованные рабочие в среднем имели малый стаж, поэтому их производительность труда была ниже необразованных рабочих, которые в среднем имели большой опыт.
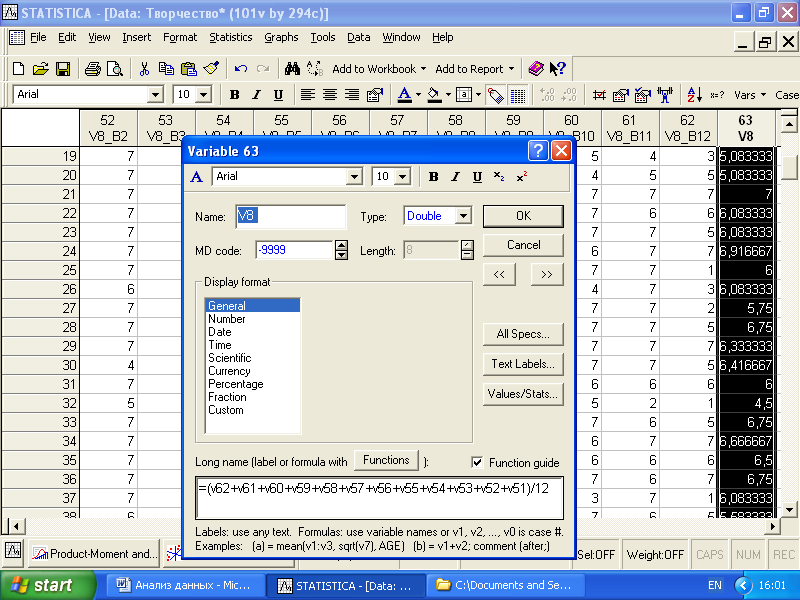
Рис. 4.15. Окно задания новой переменной
Для того чтобы исключить влияние этой третьей переменной, поступают следующим образом. Рассчитывают искомые корреляции для каждого из фиксированных уровней третьей переменной. То есть отдельно надо сопоставить между собой корреляцию образованности и производительности труда для нескольких групп рабочих: с малым, средним, большим стажем работы. После такого анализа был обнаружен совсем другой результат: более образованные рабочие имеют в среднем более высокую производительность труда.
Аналогичным образом рассчитываются коэффициенты частной корреляции, при этом исключается влияние третьей переменной на взаимосвязь исследуемых переменных.
В нашем случае будет интересно исключить влияние фактора «общий интерес к творчеству». Это позволит ярче, острее увидеть взаимодействие друг с другом отдельных групп интересов.
Создадим новую переменную-индикатор V8 (общий интерес к развитию творческой компетентности), равную усредненному значению суммы всех интересов. Для этого в главном меню нужно выбрать «Insert», а затем «Add variables».
В формуле расчета переменной V8 (рис.4.15) реализована возможность при написании формулы «=(v62+v61+v60+v59+v58+v57+v56+v55+v54 +v53+v52 +v51)/12» использовать вместо имен переменных их порядковые номера в таблице данных.
После того как новая переменная- индикатор будет создана, пересчитаем относительно ее коэффициенты корреляции для переменных V8_B1 – V8_B12. Войдем в меню «Correlations», отметим переменные для анализа в правом поле «Two lists». «First variable lists» - переменные V8_B1 – V8_B12, между которыми определим коэффициенты частной корреляции, «Second variable lists» - переменная V8, влияние которой на взаимосвязи исключается. При нажатии кнопки «Partial correlations» будет выведена корреляционная матрица.
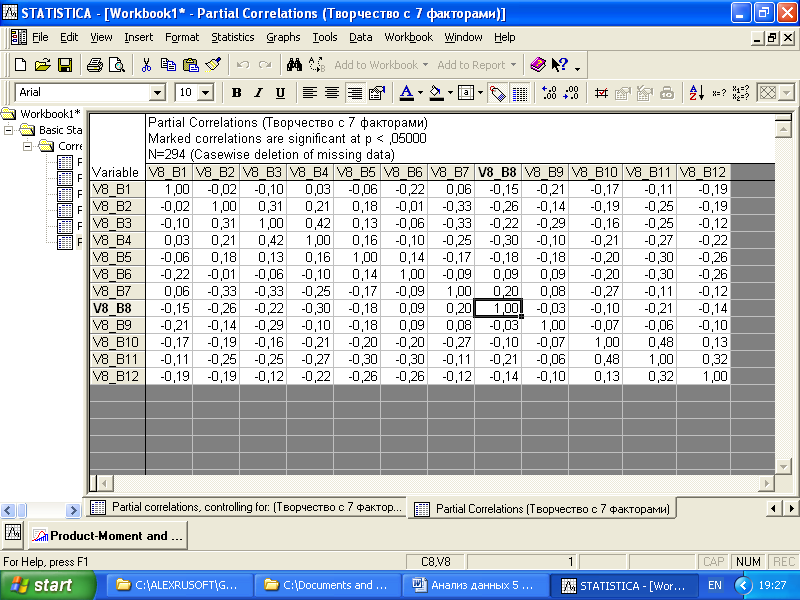
Рис. 4.16. Матрица частных корреляций
В корреляционной матрице (рис. 4.16) теперь присутствуют отрицательные коэффициенты, что свидетельствует о некотором антагонизме интересов студентов (интерес к импровизации, свободе, оригинальности идей соответствует уменьшению степени интереса к особым состояниям сознания, воображению и т. д.). По-прежнему можно выделить три группы переменных, связанных положительными корреляциями.
Таким образом, использование корреляционного анализа – кропотливая работа, требующая от исследователя системного подхода к изучаемым явлениям, знания статистических методов и процедур выявления взаимосвязей.
Задание: Проанализируйте взаимосвязи между следующими блоками переменных: знакомство с техниками творчества (V2_1 – V2_8); самооценка студентами относительно развитости своих способностей и творческих компетентностей (V8_A1 – V8_A12). Переменные V2_1 – V2_8 являются дихотомическими, поэтому к ним можно применить статистики, предназначенные для интервальных шкал. Постройте максимальный корреляционный граф. На основании статистических данных сделайте теоретические выводы.
