5. Дифференциальные уравнения второго и высших порядков.

Дифференциальные уравнения второго порядка 1. Основные понятия

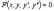Дифференциальное уравнение второго порядка можно записать в виде . Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде

.

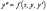Для этих уравнений имеет место теорема существования и единственности решения.

Теорема. Если в уравнении функция 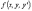и ее частные производные по аргументам y и 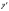непрерывны в некоторой области, содержащей 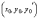, то существует и притом единственное решение 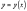уравнения, удовлетворяющее условиям 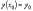и .

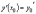Эти условия называются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости 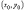с заданным тангенсом угла наклона касательной 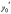проходит единственная интегральная кривая. Ясно, что если мы будем задавать различные значения , то при постоянных и 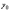мы получим бесчисленное множество интегральных кривых с различными углами наклона касательных и проходящих через заданную точку.

Общим решением дифференциального уравнения второго порядка называется функция 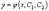, зависящая от двух произвольных постоянных, которая при любых значениях 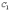и является решением дифференциального уравнения.

Уравнение , определяющее общее решение, называется общим интегралом дифференциального уравнения.

Если в общее решение подставить конкретные значения и , то получится частное решение дифференциального уравнения. График частного решения называют интегральной кривой данного дифференциального уравнения.

Рассмотрим методы решения некоторых уравнений второго порядка.

 

2. Уравнения, допускающие понижение порядка

а) рассмотрим простейшее уравнение второго порядка . Общее решение такого уравнения получается путем двукратного интегрирования:

,

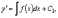
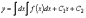где и –произвольные постоянные, а неопределенные интегралы трактуются как первообразные соответствующих функций.

Пример 7. Решить уравнение .

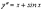Решение. Интегрируя первый раз, получаем . Общее решение данного уравнения получаем, интегрируя второй раз: .

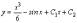б) Рассмотрим уравнение 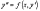, явно не содержащее искомую функцию y. Положим 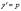. Тогда и уравнение примет вид .

Решаем теперь это уравнение первого порядка относительно p, а затем заменяем p на и решаем последнее уравнение относительно неизвестной функции y.

Пример 8. Решить уравнение .

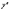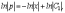
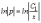Решение. Положим и подставим и в данное уравнение. Получим . Разделим переменные. Тогда . Интегрируя, получим и 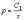. Заменим теперь p на . Имеем 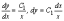и

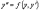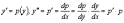в) пусть . Это уравнение явно не содержит переменную x. Подстановкой это уравнение приводят к уравнению первого порядка: .

Далее получившееся уравнение первого порядка решают относительно вспомогательной функции p, а затем, заменяя p на , получают уравнение первого порядка относительно функции y, из которого ее и находят.

Пример 9. Решить уравнение .

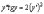Решение. Положим 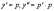, подставим в уравнение эти выражения производных и получим дифференциальное уравнение первого порядка относительно вспомогательной функции p:

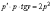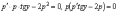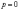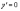. Отсюда . Это уравнение имеет решение или , а , а так же решения, удовлетворяющие уравнению .

Разделим переменные в этом уравнении:

Откуда 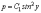. Полагая , получим дифференциальное уравнение .

Снова разделим переменные: .

Интегрируя, получим: – 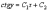или 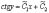. Решение уравнения p=0, то есть y=C, входит в этот общий интеграл при 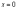, так как в таком случае и y является постоянным.

Таким образом, получили общий интеграл дифференциального уравнения 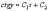, где и _–произвольные постоянные.