20. Ряд Фурье и его коэффициенты.

Определение ряда Фурье

Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функцииf (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π]. 

1. Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:

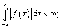
2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).  Если x₀ − точка разрыва, то ряд Фурье сходится к значению

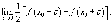
Ряд Фурье функции f (x) представляется в виде

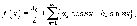
где коэффициенты Фурье a₀, a_n и b_n определяются формулами

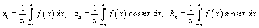
Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя a_n и b_n новыми переменными d_n и φ_n или d_n и θ_n , где

можно, соответственно, записать

21. Разложение функции в ряд Фурье. Теорема Дирихле.

Ряд Фурье — представление произвольной функции 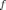с периодом в виде ряда

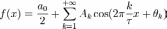
Этот ряд может быть также переписан в виде

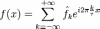
Тригонометрическим рядом Фурье функции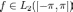 называют функциональный ряд вида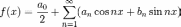 где

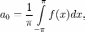
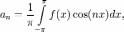
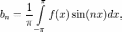
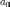
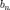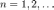Числа и ( )называются коэффициентами Фурье функции . Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию 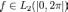в виде ряда (1), и нам надо определить неизвестные коэффициенты , и . Если умножить правую часть (1) на 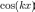и проинтегрировать по промежутку 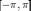, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент 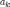. Аналогично для

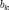
Ряд (1) сходится к функции в пространстве 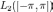. Иными словами, если обозначить через 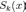частичные суммы ряда (1): 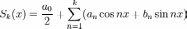то их среднеквадратичное отклонение от функции будет стремиться к нулю:

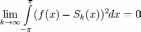
Теорема Дирихле

Признак Дирихле — теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна-Дирихле.

Признак Дирихле сходимости несобственных интегралов первого рода:

Пусть выполнены условия:

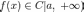• и имеет на 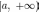ограниченную первообразную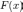 то есть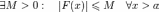

• функция

• 

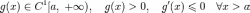
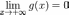
Тогда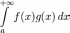 сходится.

Условие монотонности в признаке Дирихле существенно.

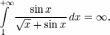
Однако, условие монотонности не является необходимым.

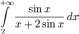
Признак Дирихле сходимости рядов Абелева типа

Ряд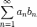 , где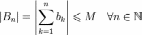 и последовательность 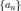— положительна и монотонна (начиная с некоторого места, хотя бы в широком смысле слова), называется рядом Абелева типа.

Теорема (признак Дирихле сходимости рядов Абелева типа)

Пусть выполнены условия:

• Последовательность частичных сумм ограничена, то есть

• 

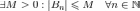
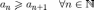
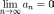• Тогда ряд сходится.

22. Определение и свойства двойного интеграла.

Определение двойного интеграла

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как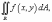

где R - область интегрирования в плоскости Oxy. Если определенный интеграл 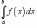от функции одной переменной 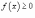выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R

Формально двойной интеграл можно ввести как предел суммы Римана. Пусть, для простоты, область интегрирования R представляет собой прямоугольник 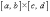. Используя ряд чисел { x0, x1, ..., xm }, разобьем отрезок [a, b] на малые интервалы таким образом, чтобы выполнялось соотношение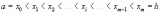

Аналогично, пусть множество чисел является разбиением отрезка [c, d] вдоль оси Oy, при котором справедливы неравенства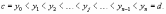

Суммой Римана функции f (x,y) над разбиением называется выражение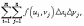

Двойной интеграл от функции f (x,y) в прямоугольной области определяется как предел суммы Римана, при котором максимальные значения Δxi и Δyj стремятся к нулю:

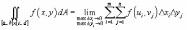
Свойства двойного интеграла:

1. 

2. 

3. 

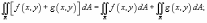
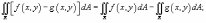
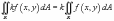
4. Если 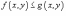в области R, то ;

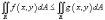5. Если 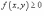в области R и 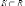то ;

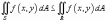6. Если на R и области R и S являются непересекающимися,то