
- •Ответы к экзамену по математическому анализу
- •Основные определения и задачи теории дифференциальных уравнений. Дифференциальные уравнения первого порядка. Теорема и задача Коши.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. Дифференциальные уравнения в полных дифференциалах. Линейные дифференциальные уравнения первого порядка
- •5. Дифференциальные уравнения второго и высших порядков.
- •6. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •7. Линейные дифференциальные уравнения второго порядка. Однородные уравнения. Определитель Вронского. Фундаментальная система решений.
- •8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •9. Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами и специальной правой частью.
- •10.Решение линейного дифференциального уравнения 2-го порядка методом Лагранжа.
- •11. Системы дифференциальных уравнений. Решение нормальной линейной системы методом характеристического уравнения.
- •– Линейные однородные системы дифференциальных уравнений – Линейные неоднородные системы дифференциальных уравнений
- •Линейные однородные системы дифференциальных уравнений
- •Что значит решить систему дифференциальных уравнений?
- •Линейные неоднородные системы дифференциальных уравнений
- •Метод характеристического уравнения (метод Эйлера)
- •12. Числовые ряды: основные определения. Геометрическая прогрессия как пример числового ряда. Основные определения и понятия.
- •13. Гармонический ряд. Необходимый признак сходимости ряда. Признаки сравнения для определения сходимости рядов с положительными членами. Числовые ряды
- •Необходимый признак сходимости ряда.
- •Достаточные признаки сходимости ряда с положительными членами
- •1. Признак Даламбера
- •2. Интегральный признак Коши
- •3. Признак сравнения рядов
- •14. Признаки сходимости Даламбера и Коши для рядов с положительными членами. Обобщенно гармонический ряд. Признак Даламбера. Радикальный признак Коши.
- •Обобщённо гармонический ряд. Ряд Дирихле:
- •Знакопеременный ряд:
- •15. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
- •16. Функциональные ряды. Точки и область сходимости. Функциональные ряды
- •17. Степенные ряды и область сходимости. Степенные ряды
- •18. Разложение функций в ряды Тейлора и Маклорена.
- •19. Применения рядов Тейлора для приближенных вычислений интегралов и решений дифференциальных уравнений.
- •20. Ряд Фурье и его коэффициенты.
- •21. Разложение функции в ряд Фурье. Теорема Дирихле.
- •22. Определение и свойства двойного интеграла.
- •23. Вычисление двойных интегралов.
- •24. Замена переменных в двойном интеграле. Полярные координаты.
- •25.Приложения двойного интеграла.
- •26. Определение тройного интеграла.
- •27. Вычисление тройного интеграла.
- •28. Замена переменных в тройном интеграле. Цилиндрические координаты.
- •29. Вычисление тройного интеграла в сферических координатах.
- •Решение
18. Разложение функций в ряды Тейлора и Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если
приведенное разложение сходится в
некотором интервале x,
т.е.
Разложение некоторых функций в ряд Маклорена
|
Пример 1 |
|
Найти
ряд Маклорена для функции Решение. Воспользуемся
тригонометрическим равенством Отсюда следует: |
Пример 2 |
|
Разложить
в ряд Тейлора функцию Решение. Вычислим производные: Видно,
что Следовательно, разложение в ряд Тейлора имеет вид |
Пример 3 |
|
Найти разложение в ряд Маклорена функции e kx, k − действительное число. Решение. Вычислим производные: Тогда в точке x = 0 получаем Следовательно, разложение данной функции в ряд Маклорена выражается формулой |
Пример 4 |
|
Найти разложение в ряд Тейлора кубической функции x3 в точке x = 2. Решение. Обозначим и
далее Таким образом, разложение в ряд Тейлора имеет вид |
Пример 5 |
|
Найти
разложение в ряд Маклорена функции Решение. Пусть При x = 0, соответственно, получаем Следовательно, разложение в ряд записывается в виде Полученное выражение называется биномиальным рядом. |
Пример 6 |
|
Найти
разложение в ряд Маклорена функции Решение. Используя
формулу биномиального ряда, найденную
в предыдущем примере, и подставляя Ограничиваясь первыми 3-мя членами, разложение можно записать в виде |
19. Применения рядов Тейлора для приближенных вычислений интегралов и решений дифференциальных уравнений.
Некоторые приложения степенных рядов.
Приближенные вычисления.
Пример.
Найти значение  с
точностью 0.001.
с
точностью 0.001.
{ Так
как это знакочередующийся ряд, то его
остаток меньше первого отброшенного
члена (гл.1,§11). Следовательно,
Так
как это знакочередующийся ряд, то его
остаток меньше первого отброшенного
члена (гл.1,§11). Следовательно, (с
точностью 0.001).}
(с
точностью 0.001).}
2. Интегрирование с помощью рядов.
Пример. 
3. Решение дифференциальных уравнений.
Примеры. 1. Найти четыре первых члена разложения в ряд Тейлора решения дифференциального
уравнения: 
{ Вычислим производные в т. х0=1:

 }
}
2*.
Решить уравнение: 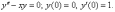
{Будем
искать решение в виде степенного ряда: 
Тогда  Подставляя
данные выражения в уравнение,
имеем:
Подставляя
данные выражения в уравнение,
имеем:  или
или 
В силу начальных условий: а0 = 0, а1 = 1. Сравнивая коэффициенты при одинаковых степенях,
получим:  Отсюда
:
Отсюда
:
 и
и 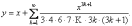 }
}



 ,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:





 .
. .
Поскольку
ряд Маклорена для cos x имеет
вид
.
Поскольку
ряд Маклорена для cos x имеет
вид  ,
то можно записать
,
то можно записать

 в
точке x
= 1.
в
точке x
= 1.
 для
всех n
≥ 3.
Для x
= 1 получаем
значения:
для
всех n
≥ 3.
Для x
= 1 получаем
значения:




 .
Тогда
.
Тогда
 для
всех x
≥ 4.
В
точке x
= 2,
соответственно, получаем
для
всех x
≥ 4.
В
точке x
= 2,
соответственно, получаем

 .
. ,
где μ −
действительное число, и x
≠ −1.
Производные будут равны
,
где μ −
действительное число, и x
≠ −1.
Производные будут равны


 .
. ,
получаем
,
получаем
