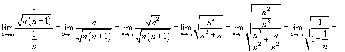- •Ответы к экзамену по математическому анализу
- •Основные определения и задачи теории дифференциальных уравнений. Дифференциальные уравнения первого порядка. Теорема и задача Коши.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. Дифференциальные уравнения в полных дифференциалах. Линейные дифференциальные уравнения первого порядка
- •5. Дифференциальные уравнения второго и высших порядков.
- •6. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •7. Линейные дифференциальные уравнения второго порядка. Однородные уравнения. Определитель Вронского. Фундаментальная система решений.
- •8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •9. Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами и специальной правой частью.
- •10.Решение линейного дифференциального уравнения 2-го порядка методом Лагранжа.
- •11. Системы дифференциальных уравнений. Решение нормальной линейной системы методом характеристического уравнения.
- •– Линейные однородные системы дифференциальных уравнений – Линейные неоднородные системы дифференциальных уравнений
- •Линейные однородные системы дифференциальных уравнений
- •Что значит решить систему дифференциальных уравнений?
- •Линейные неоднородные системы дифференциальных уравнений
- •Метод характеристического уравнения (метод Эйлера)
- •12. Числовые ряды: основные определения. Геометрическая прогрессия как пример числового ряда. Основные определения и понятия.
- •13. Гармонический ряд. Необходимый признак сходимости ряда. Признаки сравнения для определения сходимости рядов с положительными членами. Числовые ряды
- •Необходимый признак сходимости ряда.
- •Достаточные признаки сходимости ряда с положительными членами
- •1. Признак Даламбера
- •2. Интегральный признак Коши
- •3. Признак сравнения рядов
- •14. Признаки сходимости Даламбера и Коши для рядов с положительными членами. Обобщенно гармонический ряд. Признак Даламбера. Радикальный признак Коши.
- •Обобщённо гармонический ряд. Ряд Дирихле:
- •Знакопеременный ряд:
- •15. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
- •16. Функциональные ряды. Точки и область сходимости. Функциональные ряды
- •17. Степенные ряды и область сходимости. Степенные ряды
- •18. Разложение функций в ряды Тейлора и Маклорена.
- •19. Применения рядов Тейлора для приближенных вычислений интегралов и решений дифференциальных уравнений.
- •20. Ряд Фурье и его коэффициенты.
- •21. Разложение функции в ряд Фурье. Теорема Дирихле.
- •22. Определение и свойства двойного интеграла.
- •23. Вычисление двойных интегралов.
- •24. Замена переменных в двойном интеграле. Полярные координаты.
- •25.Приложения двойного интеграла.
- •26. Определение тройного интеграла.
- •27. Вычисление тройного интеграла.
- •28. Замена переменных в тройном интеграле. Цилиндрические координаты.
- •29. Вычисление тройного интеграла в сферических координатах.
- •Решение
Обобщённо гармонический ряд. Ряд Дирихле:
Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд:
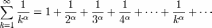
Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1.
Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:
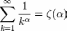
Для
чётных это значение явно выражается
через число пи, например,
 , а уже для α=3 его значение аналитически
неизвестно.
, а уже для α=3 его значение аналитически
неизвестно.
Знакопеременный ряд:
В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью. Его сумма равна натуральному логарифму 2:

Эта формула — частный случай ряда Меркатора (англ.), ряда Тейлора для натурального логарифма.
Похожий ряд может быть получен из ряда Тейлора для арктангенса:

Это известно как ряд Лейбница.
15. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что 1. an+1 < an для
всех n;
2. Тогда
знакочередующиеся ряды Абсолютная и условная сходимость Ряд |
Пример 1 |
|
Исследовать
на сходимость ряд Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем поскольку |
Пример 2 |
|
Исследовать
на сходимость ряд Решение. Попробуем применить признак Лейбница: Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится. |
Пример 3 |
Определить,
является ли ряд Решение. Применяя признак Даламбера к ряду, составленному из модулей соответствущих членов, находим Следовательно, данный ряд сходится абсолютно. |
Пример 4 |
Определить,
является ли ряд Решение. Сначала
воспользуемся признаком Лейбница и
найдем предел Таким образом, исходный ряд расходится. |
Пример 5 |
|
Исследовать на сходимость ряд Решение. Общий
член данного ряда равен Следовательно. исходный ряд сходится абсолютно. |
Пример 6 |
Исследовать,
является ли ряд Решение. Применяя признак Лейбница, видим, что ряд является сходящимся: Рассмотрим
теперь сходимость ряда Следовательно исходный ряд сходится условно. |
Пример 7 |
Определить,
является ли ряд Решение. Сначала применим признак Лейбница: Следовательно,
данный ряд сходится. Выясним, является
ли эта сходимость абсолютной или
условной. Воспользуемся предельным
признаком сравнения и сравним
соответствующий ряд из модулей Поскольку ряд , составленный из модулей, расходится, то исходный знакочередующийся ряд является условно сходящимся. |

 .
.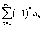 и
и 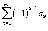 сходятся.
сходятся.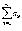 называется абсолютно
сходящимся,
если ряд
называется абсолютно
сходящимся,
если ряд  также
сходится.
Если ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится.
также
сходится.
Если ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится. 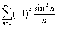 .
.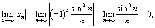
 .
Следовательно, данный ряд сходится.
.
Следовательно, данный ряд сходится. 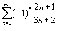 .
.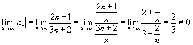
 абсолютно
сходящимся, условно сходящимся или
расходящимся?
абсолютно
сходящимся, условно сходящимся или
расходящимся?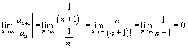
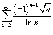 абсолютно
сходящимся, условно сходящимся или
расходящимся?
абсолютно
сходящимся, условно сходящимся или
расходящимся?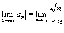 .
Вычислим этот предел по правилу
Лопиталя:
.
Вычислим этот предел по правилу
Лопиталя: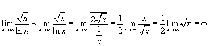
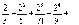
 .
Применим признак Даламбера к ряду
.
Применим признак Даламбера к ряду 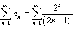 ,
составленному из модулей:
,
составленному из модулей: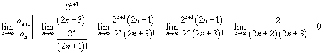
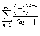 абсолютно
сходящимся, условно сходящимся или
расходящимся?
абсолютно
сходящимся, условно сходящимся или
расходящимся?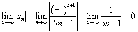
 ,
составленного из модулей соответствующих
членов. Используя интегральный признак
сходимости, получаем
,
составленного из модулей соответствующих
членов. Используя интегральный признак
сходимости, получаем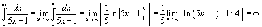
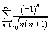 абсолютно
сходящимся, условно сходящимся или
расходящимся?
абсолютно
сходящимся, условно сходящимся или
расходящимся?
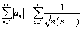 с
расходящимся гармоническим рядом
с
расходящимся гармоническим рядом 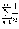 :
: