13. Гармонический ряд. Необходимый признак сходимости ряда. Признаки сравнения для определения сходимости рядов с положительными членами. Числовые ряды

Числовой ряд 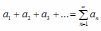задается несколькими первыми членами или формулой n-го члена

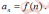
Ряд называется сходящимся, если существует предел n-ой частичной суммы:

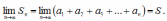
Число S называется суммой ряда.

Если 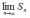не существует, то ряд называется расходящимся.

Примеры сходящихся и расходящихся рядов.

Рассмотрим ряд 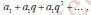( 1 )

члены которого образуют геометрическую прогрессию со знаменателем q.

Если |q|<1, то ряд сходится и его сумма

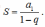
Если 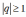, то ряд расходится.

Ряд 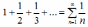называется гармоническим рядом.

Гармонический ряд расходится.

Необходимый признак сходимости ряда.

Если ряд 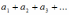сходится, то

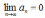
Если 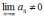(необходимый признак не выполняется), то ряд расходится.

Если 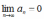(необходимый признак сходимости ряда выполняется), то для исследования ряда на сходимость надо применить какой-нибудь достаточный признак.

Пример. Исследовать ряд на сходимость с помощью необходимого признака:

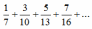
Составим формулу n-го члена ряда.Заметим, что числители дробей, как и знаменатели, образуют арифметическую прогрессию.

n-ый член арифметической прогрессии

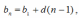
где b1– первый член, d– разность прогрессии.

Поэтому n-ый член ряда

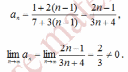
Необходимый признак сходимости не выполняется, и ряд расходится.

Достаточные признаки сходимости ряда с положительными членами

1. Признак Даламбера

Пусть в ряде с положительными членами

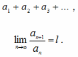
Тогда: а) если l < 1, то ряд сходится,

б) если l > 1, то ряд расходится.

При l = 1 надо использовать другой признак.

2. Интегральный признак Коши

Пусть в ряде с положительными убывающими членами

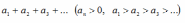
n-ый член ряда определяется формулой 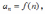где y = f(x) - непрерывная, положительная и убывающая функция на промежутке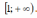 . Тогда несобственный интеграл 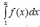и числовой ряд 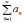одновременно сходятся или одновременно расходятся.

3. Признак сравнения рядов

Пусть даны два ряда с положительными членами, и члены первого ряда меньше соответствующих членов второго:

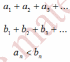
Тогда:

1) если ряд (2) сходится, то ряд (1) тоже сходится,

2) если ряд (1) расходится, то ряд (2) тоже расходится.

Итак, если члены данного ряда меньше членов сходящегося ряда, то данный ряд тоже сходится. Если члены данного ряда больше членов расходящегося ряда, то данный ряд тоже расходится.

14. Признаки сходимости Даламбера и Коши для рядов с положительными членами. Обобщенно гармонический ряд. Признак Даламбера. Радикальный признак Коши.

Признак Даламбера:

Пусть 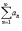− ряд с положительными членами. Тогда справедливы следующие свойства:

Если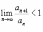 , то ряд сходится;

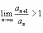Если , то ряд расходится;

Если 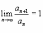, то ряд может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.

Радикальный признак Коши:

Снова рассмотрим ряд с положительными членами. Согласно признаку Коши:

Если 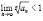, то ряд сходится;

Если 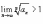, то ряд расходится;

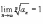Если , то вопрос о сходимости ряда , также как для признака Даламбера, остается открытым.