
МИНОБРНАУКИ РОССИИ
ОГУ
Орский гуманитарно-технологический институт (ФИЛИАЛ)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Оренбургский государственный университет»
(Орский гуманитарно-технологический институт (филиал) ОГУ)
Механико-технологический факультет
Кафедра Теплоэнергетики и теплотехники
ОТЧЕТ
по расчетно - графическому заданию
по дисциплине «Гидрогазодинамика»
_____________________________________________________________
(шифр по стандарту)
-
Руководитель
к.т.н., доцент
Ануфриенко О. С.
«_____» _______________20____г
Исполнитель
студент гр. _11TT(б) ЭОП_____
Осадчий В.Н
(подпись)
(Ф. И. О.)
2012г
20__
С ОДЕРЖАНИЕ
ОДЕРЖАНИЕ
1.1 Уравнение движения вязкой жидкости…………………….
|
3
|
2.1 Основы теории пограничного слоя………………………….
|
8
|
2.2 Уравнения пограничного слоя Л. Прандтля………………. |
10 |
|
|
2.3 Турбулизация пограничного слоя…………………………...
|
15 |
2.4 Расчет пограничного слоя по методу Кармана……………
|
17 |
Примеры решения задач…………………………………………. |
21 |
Список литературы……………………………………………….. |
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.1 Уравнение движения вязкой жидкости
При обтекании тела реальной жидкостью на его поверхности появляются касательные напряжения, обусловленные внутренним трением - вязкости. Эти напряжения возникают при относительном движении (скольжении) слоев жидкостью и всегда приводят к диссипации энергии потока, термодинамической необратимости движения, связанной с переносом количества движения (импульса) от быстрых частиц жидкости к медленным.
Чтобы получить уравнения движения вязкой жидкости, необходимо ввести дополнительные члены в уравнения движения идеальной жидкости Л. Эйлера.*) Установить вид этих членов можно, обобщая закон вязкого трения Ньютона для простейшего случая слоистого течения, когда изменение скорости течения wx происходит только по одной координате z, рисунок 1.1.

Рисунок 1.1 - Вязкие напряжения между слоями жидкости
___________________
*) Что касается уравнения непрерывности, то, как следует из его вывода, оно относится в равной мере к движению всякой жидкости, в том числе и вязкой.
Предположим сначала, что жидкость несжимаема ( = const). В этом случае, кроме нормальных сил давления - dpdydz и объемной силы Rxdxdydz, действующих в идеальной жидкости в направлении оси х (см. рисунок 2.1), в вязкой жидкости действует еще разность сил трения, касательных к верхней и нижней граням кубического объема жидкости (верхняя грань увлекается большей скоростью, нижняя тормозится меньшей):
( )верх
- (
)нижн.
)верх
- (
)нижн.
С учетом этих сил уравнение второго закона Ньютона (1.1) для частицы жидкости в проекции на ось х запишется в виде:
dxdydz
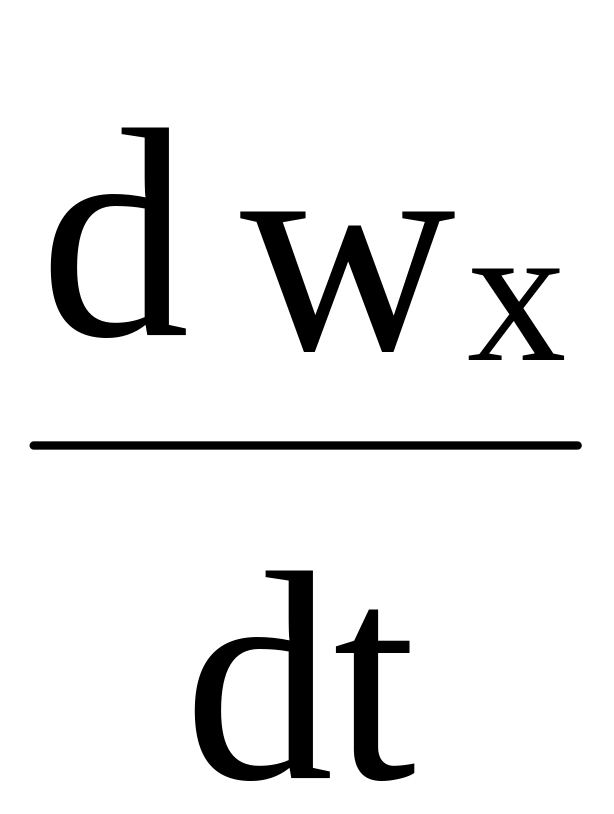 =
- dpdxdy + Rxdxdydz
+
=
- dpdxdy + Rxdxdydz
+
+ [(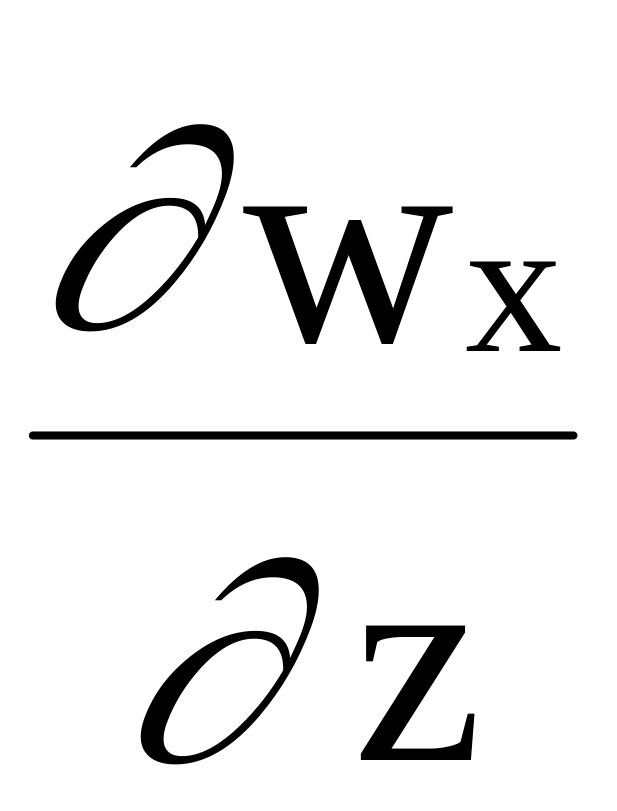 )верх
- (
)нижн]dxdy.
)верх
- (
)нижн]dxdy.
Разделив последнее равенство, на dxdydz и принимая во внимание, что , а отношение
[(
)верх
- (
)нижн]/dz
=
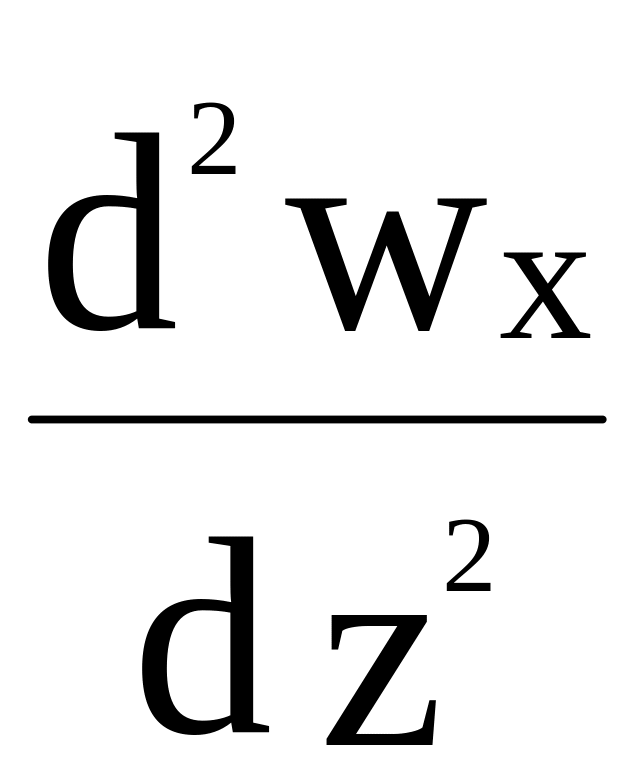 ,
,
получим:
= -
![]() + Rx
+
,
(ср. с первым
уравнением (1.11)).
+ Rx
+
,
(ср. с первым
уравнением (1.11)).
Учитывая возможность изменения вектора w и давления р в направлениях х и у, обобщим полученное уравнение на общей (3 - х мерный) случай течения несжимаемой ( = const) вязкой жидкости:
= -
![]() + Rx
+ (
+ Rx
+ (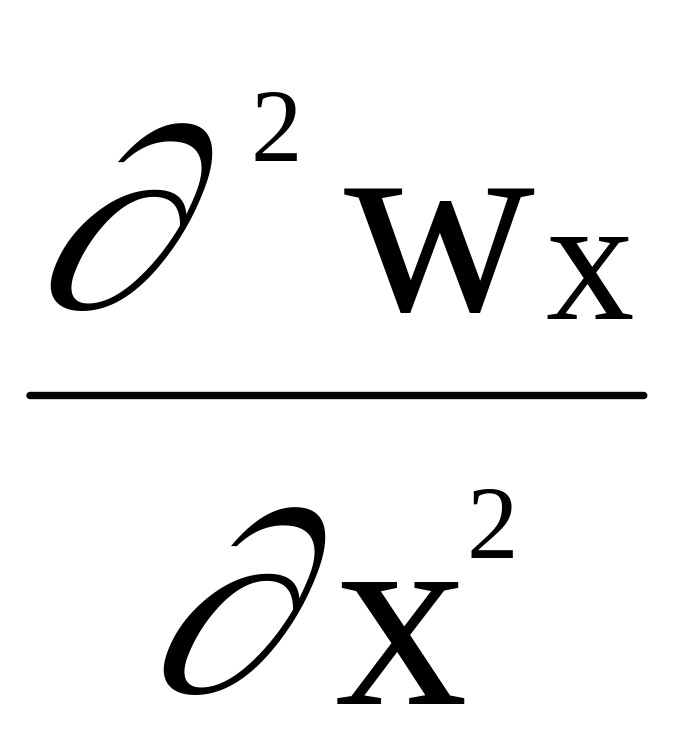 +
+
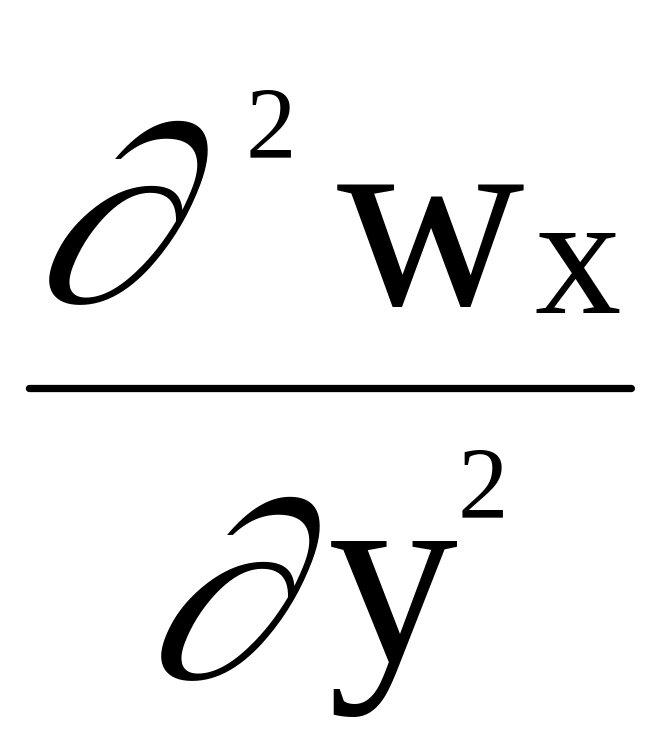 +
+
 );
);
 = -
+
Ry
+ (
= -
+
Ry
+ ( +
+
 +
+
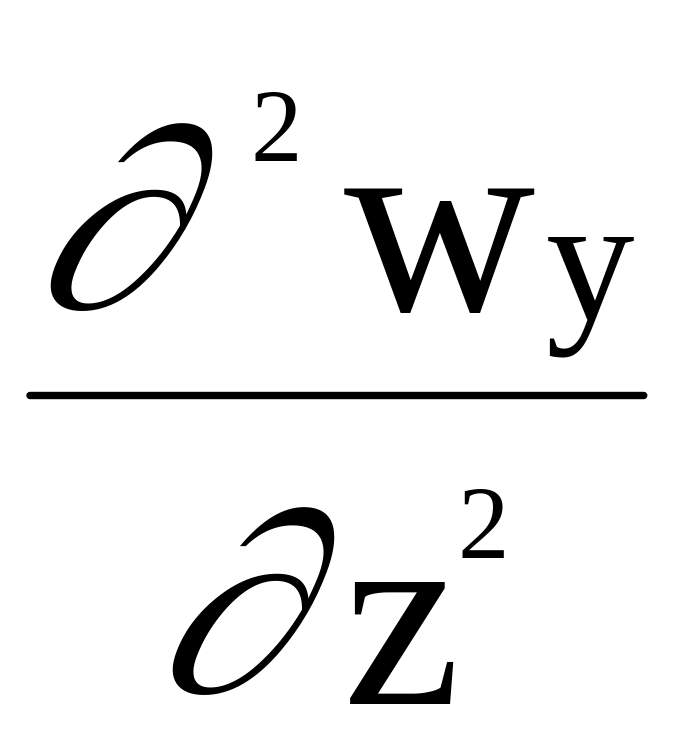 );
);
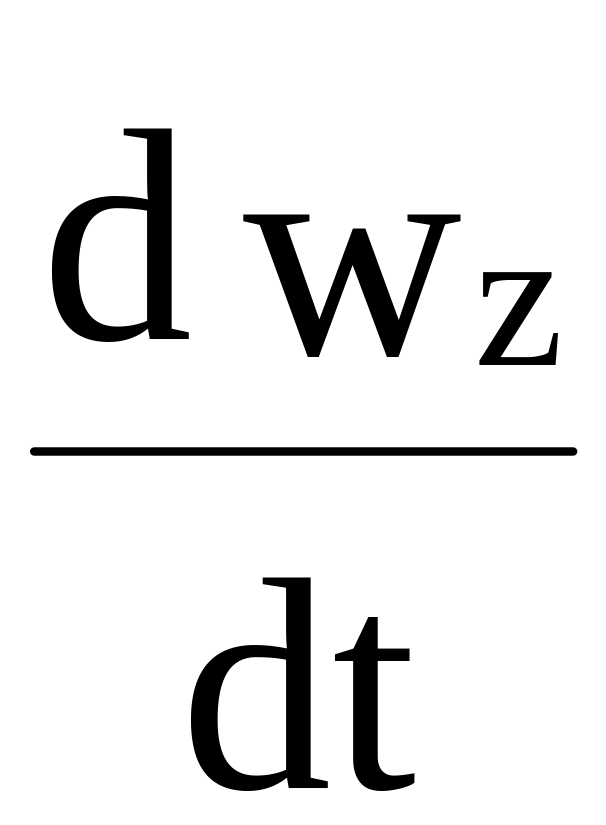 = -
+
Rz
+ (
= -
+
Rz
+ ( +
+
+
+
 )
(1.2)
)
(1.2)
или
 = --
= --
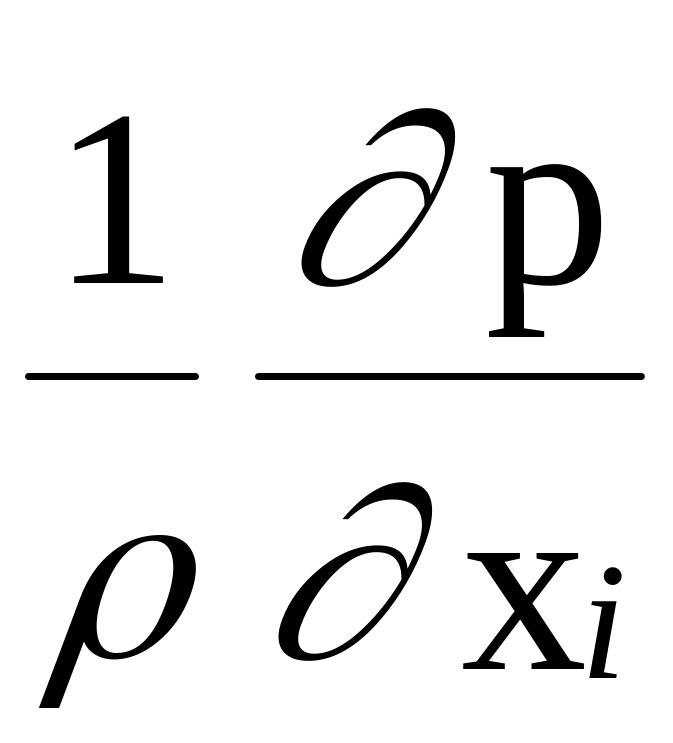 +
Ri
+
+
Ri
+ 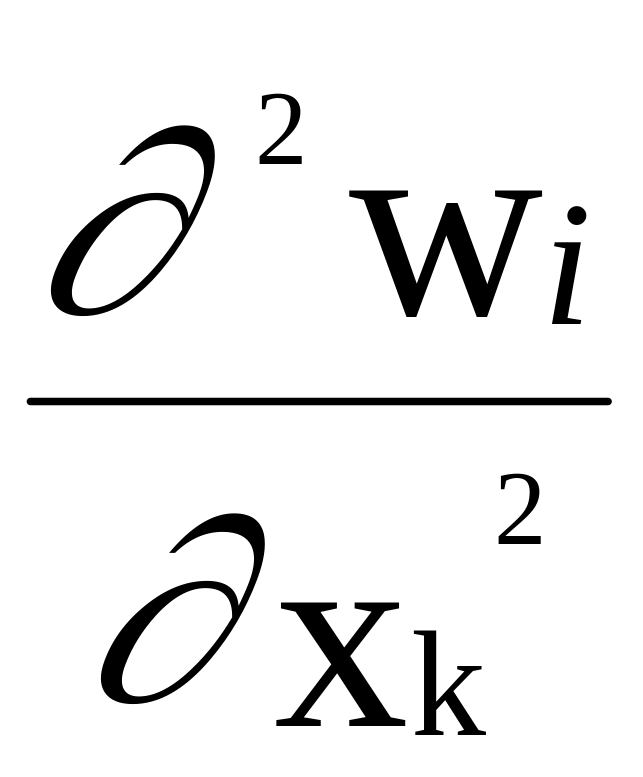 *)
(1.21)
*)
(1.21)
То же в векторном виде:
![]() = --
= --
![]() p
+
p
+
![]() +
+ ![]() .
.![]() (1.211)
(1.211)
Здесь
![]() +
+
![]() +
+
![]()
![]()
- дифференциальный оператор Лапласа.
Полученные уравнения движения вязкой несжимаемой жидкости носят название уравнений Навье - Стокса (1822; 1845).
____________________
*)
В последнем слагаемом индекс "к"
повторяется дважды (т. к.
![]()
![]() ),
является немым и по нему предполагается
суммирование.
),
является немым и по нему предполагается
суммирование.
В случае сжимаемой вязкой жидкости, когда
div w
![]()
0, для касательных
напряжений принимается :
0, для касательных
напряжений принимается :
iк
= (![]() +
+
 -
-
![]() iк
iк![]() )
+ iк
,
(1.3)
)
+ iк
,
(1.3)
где |
iк = |
{ |
1, при i = к 0, при i к
|
|
называется тензорной единицей, а коэффициент (- ) выбран так, что выражение в скобках обращается в нуль при суммировании компонент с одинаковыми индексами (i = к). Коэффициент называется вторым коэффициентом вязкости и играет заметную роль лишь при значительных изменениях плотности жидкости (например, при взрыве).
Уравнения движения
вязкой сжимаемой жидкости получаются
прибавлением производных
![]() к правой части уравнений Эйлера
к правой части уравнений Эйлера
= -
![]() + Ri
+
(1.4)
+ Ri
+
(1.4)
или, с учетом зависимости (13.3):
= -
+Ri
+
+
(
+
/3)
![]() (1.4!)
(1.4!)
Но div w, wi. Поэтому можно написать уравнение движения в векторном виде:
![]() =
- gradp + R
+ w+(
+
/3)
grad div w. (1.411)
=
- gradp + R
+ w+(
+
/3)
grad div w. (1.411)
Для несжимаемой жидкости div w = 0, = 0,что приводит к уравнению (1.2).
