6.2. Линейные преобразования и матрицы над полем.

Отображение : называется линейным оператором из в , если выполняются следующие условия.

, , , .

Определение. Матрицей размера над полем называется прямоугольная таблица, состоящая из строк и столбцов, содержащая элементов из .

Элемент матрицы индексируются номером строки и столбца , на пересечении которых он находится.

Транспонированием матрицы размера называется операция построения матрицы (другое обозначение - ) размера , где .

Суммой матриц и размера называется матрица , где . Умножение матрицы на константу производится покомпонентно.

Определение. Линейной формой над кольцом от с вектором переменных и коэффициентами , называется функция . По аналогии со скалярным произведением, для линейной формы часто используется обозначение . Заметим, что, в отличие от скалярного произведения, возможен случай , при .

Произведение матрицы размера слева на матрицу размера определено лишь в случае, когда .

В частном случае умножения матрицы-строки на матрицу-столбец , результат определяется как (т.е., при этом рассматривается как вектор).

В общем случае элемент матрицы определяется как , где - строка матрицы с номером , а - столбец матрицы с номером .

Определение. Рангом матрицы называется ранг системы ее векторов-столбцов.

Теорема. Ранг матрицы совпадает с рангом системы ее векторов-строк.

Для вычисления ранга матрицы существуют эффективные алгоритмы.

Определение. Матрица размера называется квадратной, если . Количество столбцов квадратной матрицы называется ее порядком. Заметим, что диагональю с номером квадратной матрицы порядка называется подмножество ее элементов вида , . При , диагональ называется главной, все прочие диагонали называются побочными.

Множество квадратных матриц является некоммутативным кольцом относительно введенных выше операций сложения и умножения.

Нулем является матрица , состоящая из всех нулей. Единицей - матрица , у которой все элементы главной диагонали равны единице, а прочие элементы - нулю.

Очевидно, умножение квадратной матрицы порядка на матрицу-столбец дает матрицу-столбец, и эту операцию можно рассматривать как операцию над векторами. Легко проверить, что такая операция является линейным преобразованием - мерного векторного пространства. Для матрицы такое преобразование является взаимно однозначным. Итак, взаимнооднозначные матричные преобразования существуют. Соответствующие матрицы называются обратимыми.

Определение. Пусть - обратимая матрица. Матрицей обратной к называется матрица , для которой выполняются условия .

Примером обратимых матриц являются подстановочные матрицы.

6.3. Подстановочные матрицы. Определитель матрицы над .

Определение. Подстановкой порядка на множестве из элементов называется взаимно однозначное отображение множества на себя.

Пусть упорядочено, тогда ему соответствует последовательность номеров . После применения подстановки порядок элементы порядок следования элементов изменится и примет вид .

Подстановку можно представить в виде двустрочной записи: . Очевидно, обратное преобразование имеет вид .

Рассмотрим квадратную матрицу порядка , у которой элементы с индексами равны единице, а прочие равны нулю. Например, для подстановки , получим .

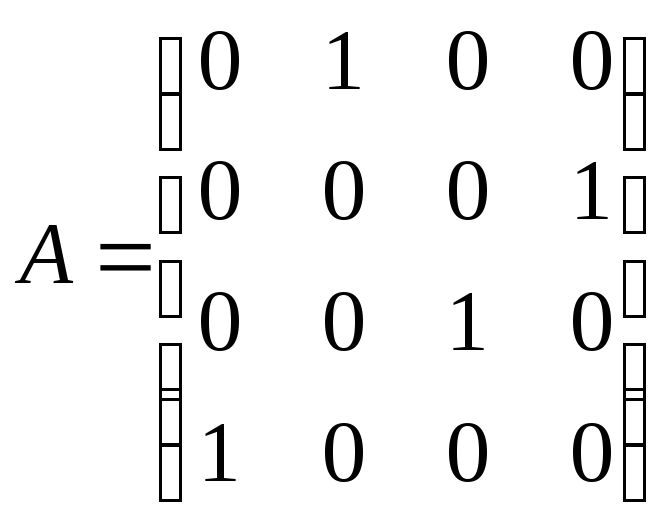Очевидно, , т.е. матрица реализует заданную подстановку. Исходя из определения подстановки, подстановочные матрицы обратимы. Если матрица - подстановочная, то .

В общем случае, легко видеть, что матрица обратима, если ее столбцы линейно независимы.

Критерий обратимости матрицы формулируется с помощью понятия определителя (детерминанта). Детерминант матрицы над полем является элементом поля . Он является функцией всех элементов матрицы и обозначается через . Детерминант записывается также в виде .

Матрица обратима тогда и только тогда, когда .

Вычисление детерминанта с помощью ЭВМ является сравнительно легкой задачей.

Общее определение детерминанта мы дадим несколько позже, а сейчас рассмотрим случай, когда матрица порядка определена над полем .

Рассмотрим все подстановочных матриц порядка . Представим себе, что каждая из них записана в виде таблицы на отдельном листе бумаги в клетку. Вырежем в каждой таблице окошки в тех клетках, где элементы соответствующей матрицы равны единице. Получим, таким образом, совокупность подстановок в виде трафаретов.

Наложим каждый трафарет на матрицу и перемножим все появившиеся в окошках элементы матрицы . Результат назовем членом определителя матрицы, соответствующим подстановке .

Найдем сумму по модулю два всех членов определителя. Результат назовем определителем матрицы над полем .

Определитель используется, в частности, для построения матрицы, обратной .