Площадь поверхности усеченного конуса

1. Площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса.

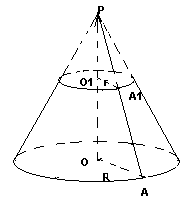
Пусть Р – вершина конуса, из которого получен усеченный конус, АА1-одна из образующих

Усеченного конуса О и О1 – центры оснований. Используя формулу Sбок для конуса получаем

S бок =   πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда, учитывая, что AA1=L, находим

Sбок =πrL +π (r - r1)PA1

Выразим РА1 через L1, r и  r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р и поэтому PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем  PA1=Lr1/R-r1.  S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1) 

Sбок =πL(r+r1)

2.    Площадь полной поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и оснований

  Sполн = S1+S2+Sбок=πL(r+r1)+ πR²+πr²

Обьем усеченного конуса

Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса.. Обьем усеченного конуса V, высота которого равна h, а площади оснований S и S1 вычисляется по формуле

V=1/3h(S+S1+√S*S1)

рисунок 8                    рисунок  9

Касательной  плоскостью  к  конусу  называется  плоскость, проходящая через образующую  конуса  и  перпендикулярная плоскости   осевого   сечения,   содержащей   эту   образующую

За величину боковой поверхности конуса (полного или усеченного) принимается предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды (полной или усеченной), когда число сторон правильного многоугольника, вписанного в основание, неограниченно увеличивается (и, следовательно, площадь каждой боковой грани неограниченно убывает).

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

В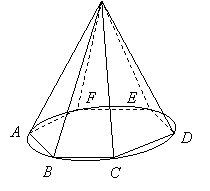 пишем в конус какую-нибудь правильную пирамиду. Пусть p - длина периметра основания, l - длина апофемы пирамиды, L - образующая конуса. Предположим, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр p будет стремиться к пределу, принимаемому за длину окружности основания C, а апофема l будет иметь пределом образующую конуса, значит боковая поверхность вписанной пирамиды, равная , будет стремиться к пределу . Этот предел и принимается за величину боковой поверхности конуса, то есть .

Чтобы получить полную поверхность конуса, достаточно приложить к боковой поверхности площадь основания: .

Теоремы:. Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность  - по окружности с центром на оси конуса. Доказательство. Пусть    - плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость    с плоскостью основания, совмещает сечение конуса плоскостью    с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана.

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Теоремы: 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

Доказательство.

В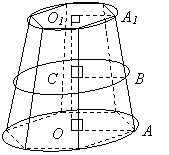 пишем в усеченный конус какую-нибудь правильную усеченную пирамиду. Пусть p - периметр нижнего основания,  - периметр верхнего, l - длина апофемы пирамиды,

L - образующая усеченного конуса. При неограниченном возрастании числа боковых граней вписанной пирамиды периметры p и  стремятся к пределам, принимаемым за длины окружностей оснований C и , а апофема l имеет пределом образующую L => величина боковой поверхности вписанной пирамиды, равная , будет стремиться к пределу . Этот предел и принимается за величину боковой поверхности усеченного конуса, то есть .

Чтобы получить полную поверхность усеченного конуса, достаточно приложить к боковой поверхности сумму площадей двух оснований: .

Следствие:

Если в трапеции , от вращения которой получается конус, провести среднюю линию BC, то  =>  => .